Интеграл. Формула Ньютона-Лейбница

Цель урока:
Ввести понятие интеграла и его вычисление по формуле Ньютона – Лейбница, используя знания о первообразной и правила её вычисления;
Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции;
Закрепить изученное в ходе выполнения упражнений.

Определение:
Пусть дана положительная функция f(x), определенная на конечном отрезке [a;b].
Интегралом от функции f(x) на [a;b] называется площадь её криволинейной трапеции.

Обозначение:
⎯ «интеграл от a до b эф от икс дэ икс»

Историческая справка:
Обозначение интеграла Лейбниц произвёл от первой буквы слова «Сумма» (Summa). Ньютон в своих работах не предложил альтернативной символики интеграла, хотя пробовал различные варианты. Сам термин интеграл придумал Якоб Бернулли.
Summa

Обозначение неопределённого интеграла ввёл Эйлер.
Оформление определённого интеграла в привычном нам виде придумал Фурье.

Формула Ньютона - Лейбница

Пример 1.
Вычислить определённый интеграл:
=
Решение:

Пример 2.
Вычислите определённые интегралы:
5
9
1

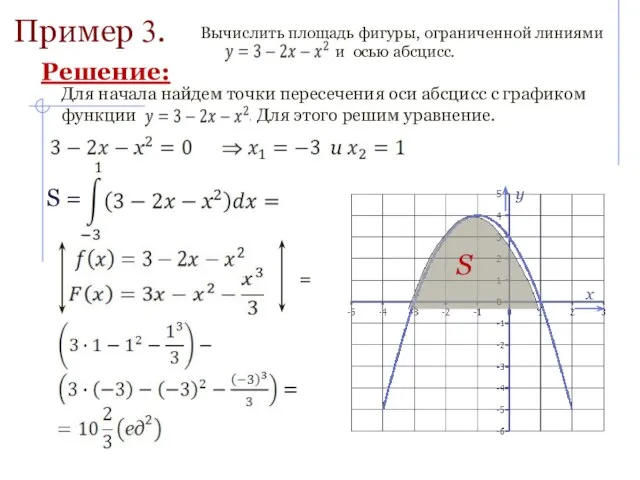
Пример 3.
=
Решение:
S =

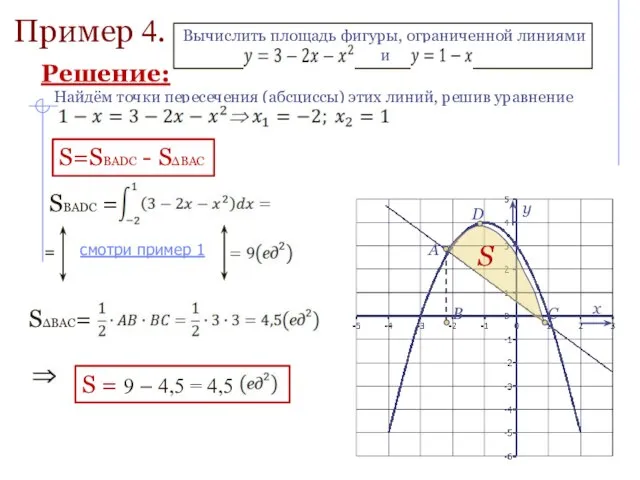
Пример 4.
Найдём точки пересечения (абсциссы) этих линий, решив уравнение
S=SBADC - SΔBAC
SBADC =
=
SΔBAC=
Решение:

ПРАВИЛА СИНКВЕЙНА
1строка – тема синквейна 1 слово
2строка – 2 прилагательных, описывающих признаки и свойства темы
3строка – 3 глагола описывающие характер действия
4строка – короткое предложение из 4 слов, показывающее Ваше личное отношение к теме
5строка – 1 слово, синоним или Ваша ассоциация тема предмета.

Интеграл
2. Определённый, положительный
Считают, прибавляют, умножают
4. Вычисляют формулой Ньютона - Лейбница
5. Площадь

Список используемой литературы:
учебник Колмагорова А.Н. и др. Алгебра и начала анализа 10 - 11 кл.

СПАСИБО ЗА ВНИМАНИЕ!
« ТАЛАНТ –
это 99% труда и 1% способности»
народная мудрость