и котангенса. возьмем любой прямоугольный треугольник. Из курса геометрии мы знаем, что у него есть два катета и гипотенуза, причем угол между двумя катетами прямой - то есть равен 90o, или π/2 радиан.
Рассмотрим угол α, который образован одним из катетов и гипотенузой.
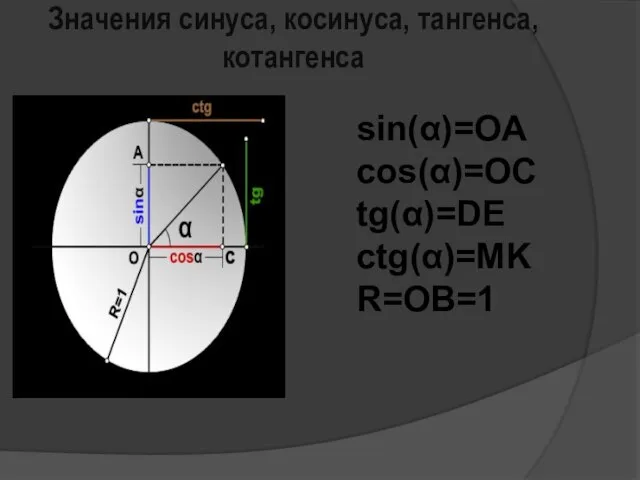
Синусом угла α называется отношение длин противолежащего катета к гипотенузе.
Косинусом угла α называется отношение длин прилежащего катета к гипотенузе.
Тангенсом угла α называется отношение длин противолежащего катета к прилежащему.
Котангенсом угла α называется отношение длин прилежащего катета к противолежащему.
Из определений тригонометрических функций сразу же следуют тригонометрические тождества:






 Применение математики в экономических исследованиях
Применение математики в экономических исследованиях Л.10_Непрерывность функции
Л.10_Непрерывность функции Деление десятичных дробей
Деление десятичных дробей Случаи вычитания
Случаи вычитания Решение задач
Решение задач Объёмные и плоские предметы. 1 класс
Объёмные и плоские предметы. 1 класс Задачи с инструкцией для решения по теме: объем пирамиды
Задачи с инструкцией для решения по теме: объем пирамиды Тренды графического дизайна
Тренды графического дизайна Теорема Виета. Урок систематизации, обобщения и контроля знаний
Теорема Виета. Урок систематизации, обобщения и контроля знаний Перпендикуляр. Определение
Перпендикуляр. Определение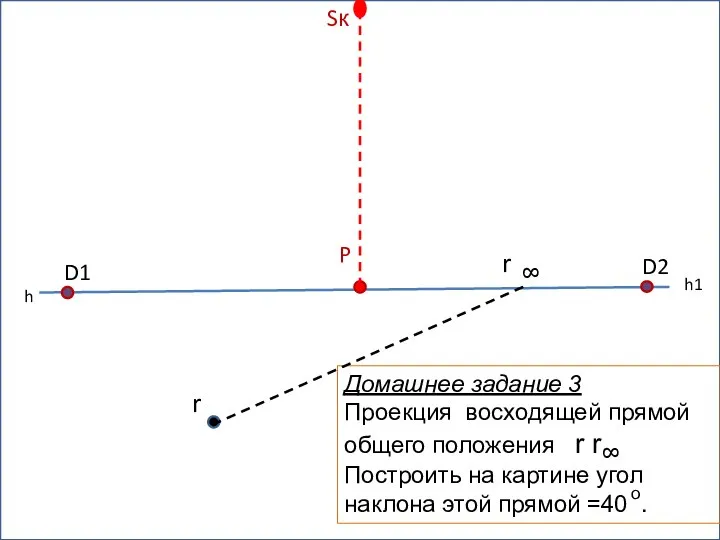 Проекция восходящей прямой общего положения r r
Проекция восходящей прямой общего положения r r Равнобедренный треугольник. Свойства равнобедренного треугольника
Равнобедренный треугольник. Свойства равнобедренного треугольника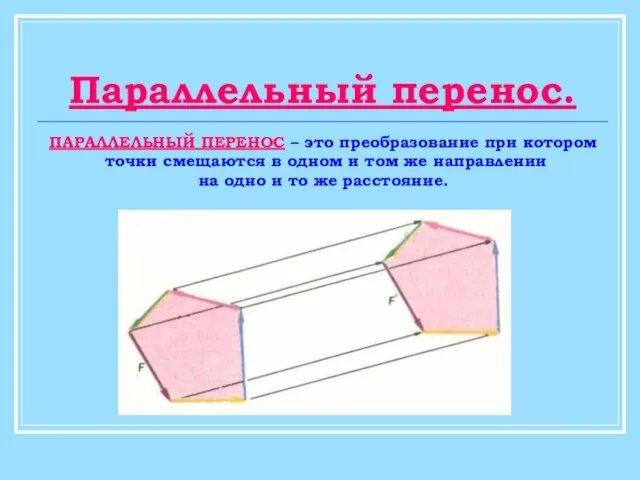 Параллельный перенос фигур
Параллельный перенос фигур Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Презентация учебного проекта Автор: Зрянина Татьяна Ивановна, учитель математики
Презентация учебного проекта Автор: Зрянина Татьяна Ивановна, учитель математики округление натуральных чисел 5 класс презентация
округление натуральных чисел 5 класс презентация Степень числа
Степень числа Случаи сложения вида +5 с переходом через десяток
Случаи сложения вида +5 с переходом через десяток Правильный тетраэдр
Правильный тетраэдр Подготовка к ЕГЭ
Подготовка к ЕГЭ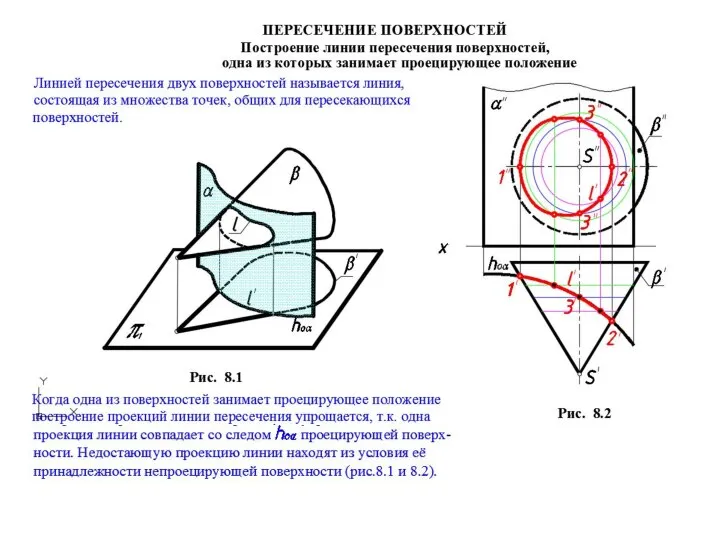 Пересечение поверхностей. Лекция 8,9,10
Пересечение поверхностей. Лекция 8,9,10 7. На сколько больше. На сколько меньше
7. На сколько больше. На сколько меньше Математические ребусы
Математические ребусы Задачи на части
Задачи на части Вероятность случайного события
Вероятность случайного события Нестандартный урок математики. Проведен учителем I категории Крутько В.И.
Нестандартный урок математики. Проведен учителем I категории Крутько В.И. Дифференциальные уравнения и их применение в медицине
Дифференциальные уравнения и их применение в медицине Введение в геометрию
Введение в геометрию