Слайд 2Первообразная функции
Функция F(x) называется первообразной для функции f(x), если выполняется равенство F’(x)=f(x)
Нахождение

первообразной для данной функции называется интегрированием функции
Свойства первообразной
Если F(x) является первообразной для функции f(x), то и функции F(x)+c тоже является первообразной для f(x), где c–это константа.
Если F1 (x) и F2(x) первообразные функции f(x), то они отличаются на константу, т. е. F1(x)-F2(x) = c
Слайд 3Неопределенный интеграл
Совокупность всех первообразных называется неопределенным интегралом
Свойства неопределенного интеграла:
1.

Слайд 7Методы интегрирования
Непосредственное интегрирование
Интегралы вычисляются с помощью свойств и табличных формул
Пример:

Слайд 82. Замена переменной
Для вычисления интегралов вводится новая переменная t, через которую выражается

исходная функция f(x) и исходный дифференциал dx. Вычисляется интеграл относительно новой переменной t, получается первообразная F(t) и делается обратная замена – выражаем t через выражение содержащее x
Пример:
Слайд 93. Интегрирование по частям
Для вычисления интегралов используется формула:
где u и dv части

исходного интеграла. Чтобы применить формулу необходимо найти v и du, применяя формулы для нахождения дифференциала и интеграла
Пусть u = f(x), тогда du = f’(x)dx;
dv = g(x)dx, следовательно v = ∫g(x)dx
Слайд 10Пример:
u = sin x | du = (sin x)’dx = cos x dx
dv
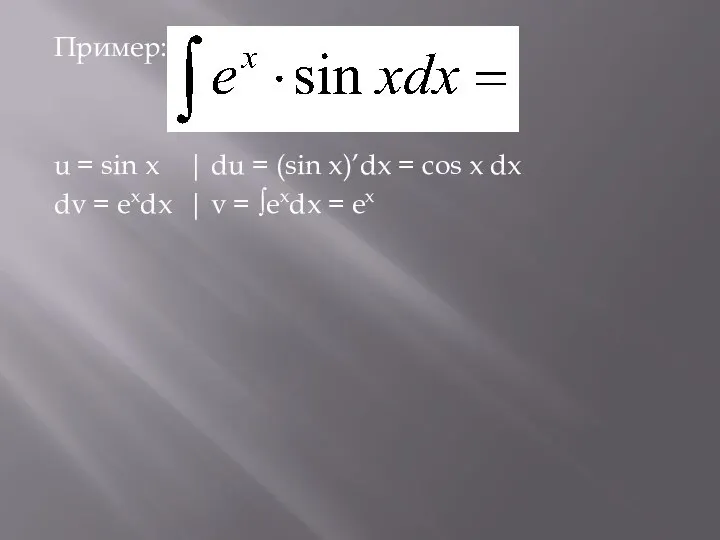
= exdx | v = ∫exdx = ex
Слайд 11Определённый интеграл
Интеграл взятый на определенном отрезке называется определенным интегралом
a и b –

пределы интегрирования, a – нижний предел, b – верхний предел (a < b)
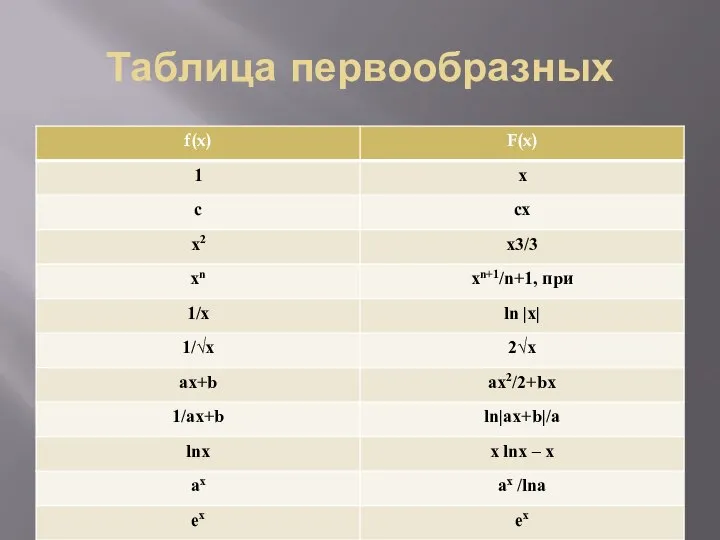
Для решения определенного интеграла применяется формула Ньютона-Лейбница:
Слайд 12Свойства определенного интеграла
1.
2.
3.
4. Если f(x) ≤ g(x) на интервале [a; b], то
![Свойства определенного интеграла 1. 2. 3. 4. Если f(x) ≤ g(x) на интервале [a; b], то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1115964/slide-11.jpg)
Слайд 13Применение определённого интеграла
Нахождение площади фигуры, ограниченной функцией (функциями):
где f(x) ограничивает фигуру сверху,

g(x) ограничивает фигуру снизу
Слайд 142. Нахождение объёма тела вращения, ограниченного функцией:
3. Нахождение длины дуги кривой:

Слайд 15Дифференциальные уравнения
Уравнения содержащие аргумент, функцию и её производные называются дифференциальными уравнениями
Решением

дифференциального уравнения является функция y = φ (x; c), где c – константа.
При решении дифференциального уравнения производная заменяется на отношение дифференциалов:


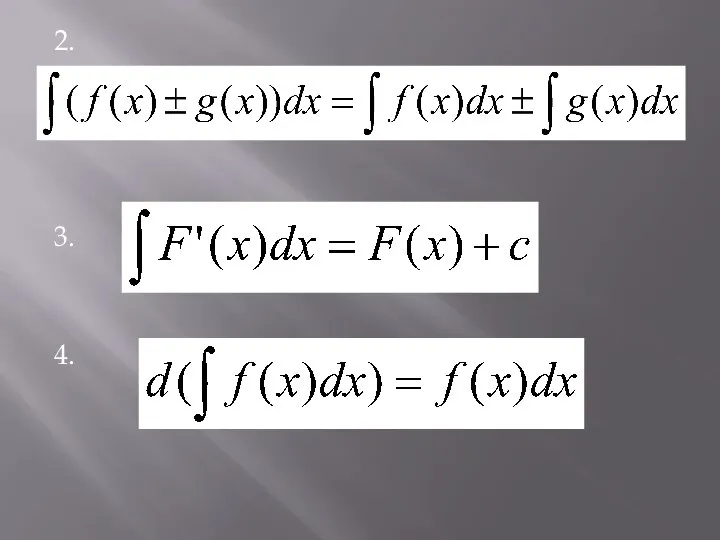




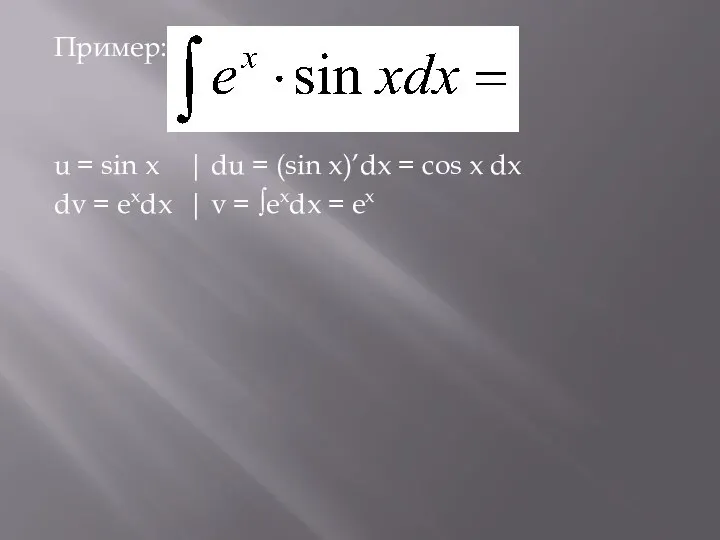

![Свойства определенного интеграла 1. 2. 3. 4. Если f(x) ≤ g(x) на интервале [a; b], то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1115964/slide-11.jpg)



 Презентация на тему Аксиома параллельных прямых
Презентация на тему Аксиома параллельных прямых  Презентация на тему ЗАДАЧИ НА ДРОБИ
Презентация на тему ЗАДАЧИ НА ДРОБИ 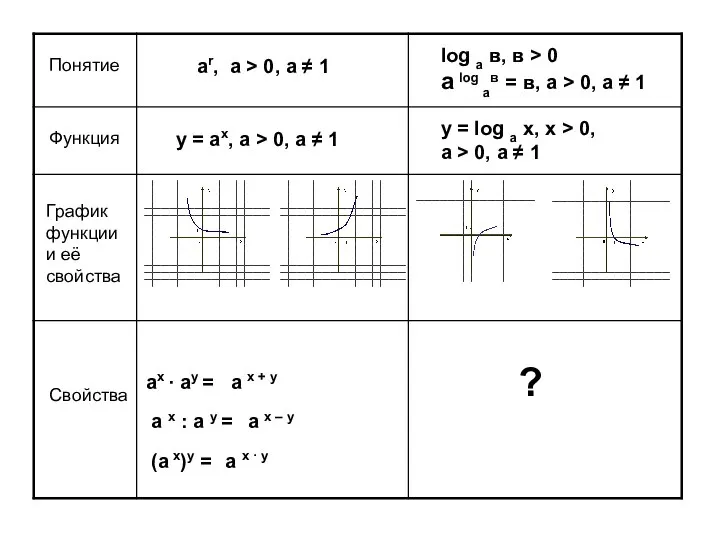 Свойства логарифмов
Свойства логарифмов Устный счёт. Состав числа 6. 1 класс
Устный счёт. Состав числа 6. 1 класс Sluchaynye_velichiny_14_sen
Sluchaynye_velichiny_14_sen Действительный анализ
Действительный анализ Математика. Задания по учебнику
Математика. Задания по учебнику Математическая викторина
Математическая викторина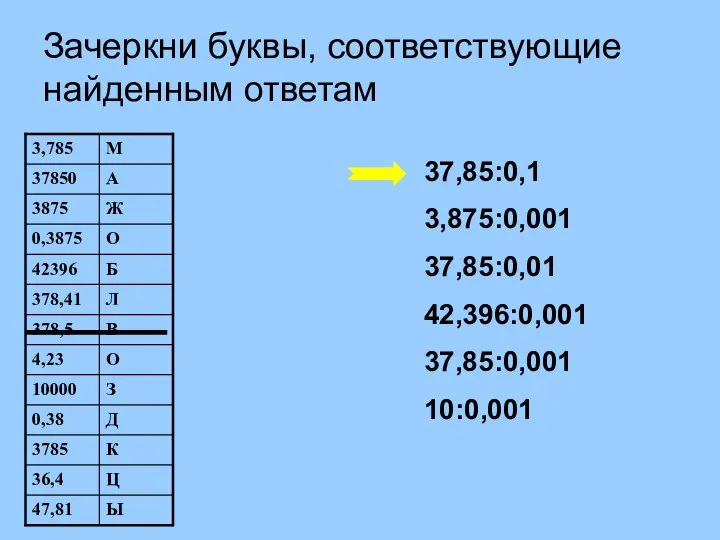 Устная работа (1). Зачеркни буквы, соответствующие найденным ответам
Устная работа (1). Зачеркни буквы, соответствующие найденным ответам Комплексные числа. Понятие мнимой единицы. Алгебраическая форма комплексного числа. Последовательности
Комплексные числа. Понятие мнимой единицы. Алгебраическая форма комплексного числа. Последовательности Задачи на готовых чертежах: Перпендикулярность плоскостей
Задачи на готовых чертежах: Перпендикулярность плоскостей Прямоугольник, ромб, квадрат
Прямоугольник, ромб, квадрат Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Разминка. Подготовка к ГИА
Разминка. Подготовка к ГИА Площадь параллелограмма
Площадь параллелограмма Сравнение чисел
Сравнение чисел Комбинаторика
Комбинаторика Презентация на тему Линейная функция 6 класс
Презентация на тему Линейная функция 6 класс  Задачи на кратное сравнение
Задачи на кратное сравнение Градусная мера дуги окружности. Теорема о вписанном угле
Градусная мера дуги окружности. Теорема о вписанном угле Геометриялық фигуралар
Геометриялық фигуралар Презентация по математике "Табличное умножение и деление" -
Презентация по математике "Табличное умножение и деление" -  Квадратные корни. 8 класс
Квадратные корни. 8 класс Психолого – педагогические основы организации математического развития младших школьников
Психолого – педагогические основы организации математического развития младших школьников Базіс лінейнай прасторы. Каардынаты
Базіс лінейнай прасторы. Каардынаты Перпендикулярность плоскостей. 10 класс
Перпендикулярность плоскостей. 10 класс Функции и их графики. 9 класс
Функции и их графики. 9 класс Задачи на нахождение неизвестного
Задачи на нахождение неизвестного