Презентация

Понятие вектора
Векторная величина (или вектор) — физическая величина, характеризующаяся не только своим числовым значением, но и направлением в пространстве.
Рассмотрим произвольный отрезок. Его концы называются граничными точками отрезка.
На отрезке можно указать два направления: от одной граничной точки к другой и наоборот. Чтобы выбрать одно из этих направлений, одну граничную точку отрезка назовем началом отрезка, а другую — концом отрезка и будем считать, что отрезок направлен от начала к концу.

Определение
Отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом, называется направленным отрезком или вектором.
Любая точка плоскости является вектором. В этом случае вектор называется нулевым.
Длиной или модулем ненулевого вектора называется длина отрезка AB. Длина вектора (вектора ) обозначается так: | |(| |). Длина нулевого вектора считается равной нулю: | | | = 0.

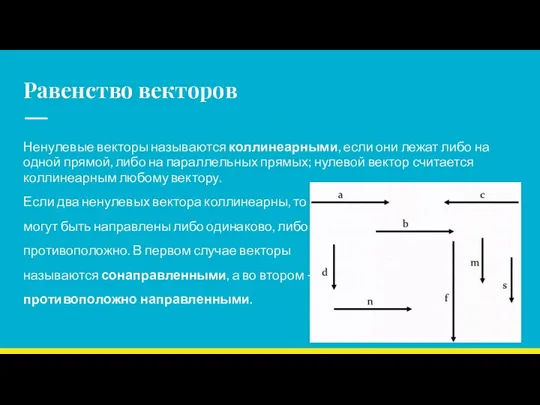
Равенство векторов
Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых; нулевой вектор считается коллинеарным любому вектору.
Если два ненулевых вектора коллинеарны, то они
могут быть направлены либо одинаково, либо
противоположно. В первом случае векторы
называются сонаправленными, а во втором —
противоположно направленными.

Определение
Векторы называются равными, если они сонаправлены и их длины равны.
Сонаправленность векторов обозначается следующим образом ↑ ↑ .

Откладывание вектора от данной точки
Если точка A — начало вектора , то говорят, что вектор отложен от точки A.
Докажем следующее утверждение: от любой точки M можно отложить вектор, равный данному вектору , а притом только один.
В самом деле, если — нулевой вектор, то искомым вектором является вектор MM.
Равные векторы, отложенные от разных точек, часто обозначают одной и той же буквой. Иногда про такие векторы говорят, что это один и тот же вектор, но отложенный от разных точек.

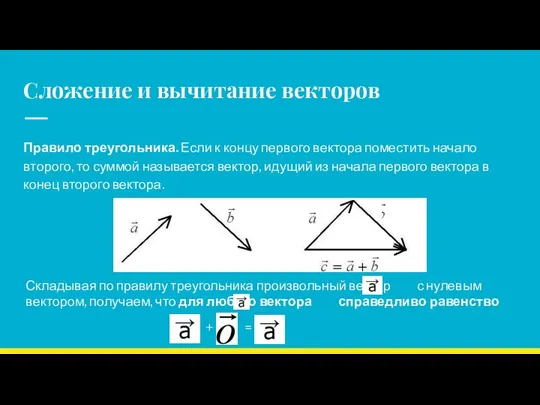
Сложение и вычитание векторов
Правило треугольника. Если к концу первого вектора поместить начало второго, то суммой называется вектор, идущий из начала первого вектора в конец второго вектора.
Складывая по правилу треугольника произвольный вектор с нулевым вектором, получаем, что для любого вектора справедливо равенство
+
=

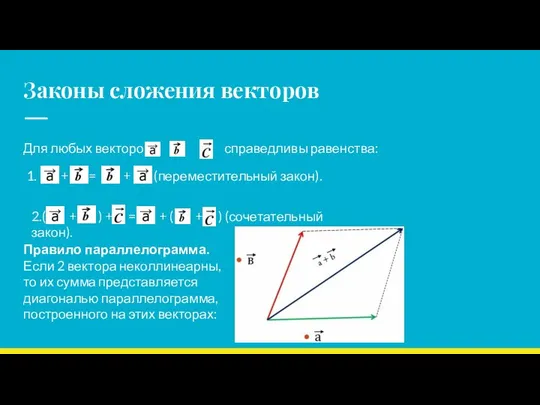
Законы сложения векторов
Для любых векторов , и справедливы равенства:
+
= + (переместительный закон).
2.( + ) + = + ( + ) (сочетательный закон).
Правило параллелограмма. Если 2 вектора неколлинеарны, то их сумма представляется диагональю параллелограмма, построенного на этих векторах:

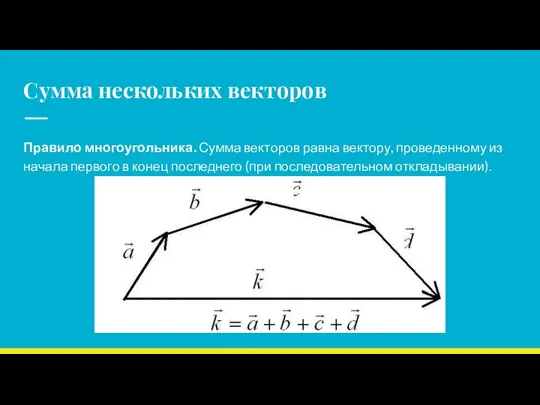
Сумма нескольких векторов
Правило многоугольника. Сумма векторов равна вектору, проведенному из начала первого в конец последнего (при последовательном откладывании).

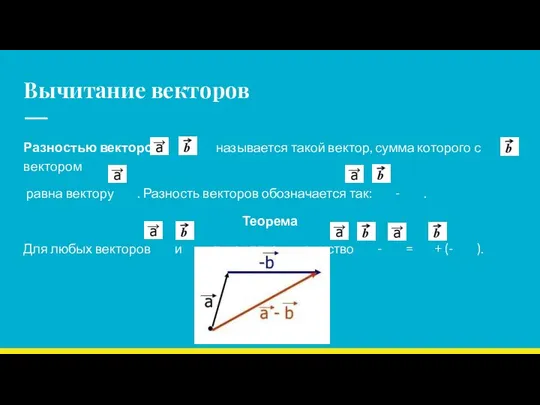
Вычитание векторов
Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору . Разность векторов обозначается так: - .
Теорема
Для любых векторов и справедливо равенство - = + (- ).

Умножение вектора на число
Из определения произведения вектора на число непосредственно следует, что:
произведение любого вектора на число нуль есть нулевой вектор;
для любого числа k и любого вектора векторы и k коллинеарны.

Средняя линия трапеции
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.