- Главная
- Математика
- Булева логика

Содержание
Слайд 2Логические выражения можно преобразовывать в соответствии с законами алгебры логики:
Законы рефлексивности
a ∨ a
Логические выражения можно преобразовывать в соответствии с законами алгебры логики:
Законы рефлексивности a ∨ a

= a
a ∧ a = a
Законы коммутативности
a ∨ b = b ∨ a a ∧ b = b ∧ a
Законы ассоциативности (a ∧ b) ∧ c = a ∧ (b ∧ c) (a ∨ b) ∨ c = a ∨ (b ∨ c)
Законы дистрибутивности a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c) a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c)
Закон отрицания отрицания ¬ (¬ a) = a
Законы де Моргана ¬ (a ∧ b) = ¬ a ∨ ¬ b ¬ (a ∨ b) = ¬ a ∧ ¬ b
Законы поглощения a ∨ (a ∧ b) = a a ∧ (a ∨ b) = a
Законы коммутативности
a ∨ b = b ∨ a a ∧ b = b ∧ a
Законы ассоциативности (a ∧ b) ∧ c = a ∧ (b ∧ c) (a ∨ b) ∨ c = a ∨ (b ∨ c)
Законы дистрибутивности a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c) a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c)
Закон отрицания отрицания ¬ (¬ a) = a
Законы де Моргана ¬ (a ∧ b) = ¬ a ∨ ¬ b ¬ (a ∨ b) = ¬ a ∧ ¬ b
Законы поглощения a ∨ (a ∧ b) = a a ∧ (a ∨ b) = a
Слайд 3Сводная таблица
Законы коммутативности (переместительный)
a v b = b v a a ∧
Сводная таблица
Законы коммутативности (переместительный)
a v b = b v a a ∧

b = b ∧ a
Законы ассоциативности (сочетательный)
a v (b v c)=(a v b) v c а∧ (b ∧ c)=(a ∧ b) ∧ c
Законы дистрибутивности (распределительный)
a v (b ∧ c)=(a v b) ∧ (a v c) a ∧ (b v c)=(a ∧ b) v (a ∧ c)
a v b ∧ c=(a v b) ∧ (a v c) a ∧ (b v c)=a ∧ b v a ∧ c
Дополнение
a v ¬ a = 1 a ∧ ¬ a = 0
Законы де Моргана
¬ (a v b) = ¬ a ∧ ¬ b ¬ (a ∧ b) = ¬ a v ¬ b
Законы поглощения
a v (a ∧ b)=a a ∧ (a v b)=a
Законы ассоциативности (сочетательный)
a v (b v c)=(a v b) v c а∧ (b ∧ c)=(a ∧ b) ∧ c
Законы дистрибутивности (распределительный)
a v (b ∧ c)=(a v b) ∧ (a v c) a ∧ (b v c)=(a ∧ b) v (a ∧ c)
a v b ∧ c=(a v b) ∧ (a v c) a ∧ (b v c)=a ∧ b v a ∧ c
Дополнение
a v ¬ a = 1 a ∧ ¬ a = 0
Законы де Моргана
¬ (a v b) = ¬ a ∧ ¬ b ¬ (a ∧ b) = ¬ a v ¬ b
Законы поглощения
a v (a ∧ b)=a a ∧ (a v b)=a
Слайд 4с
a v (¬ a ∧ b) = a v b a ∧
с
a v (¬ a ∧ b) = a v b a ∧

(¬ a v b)= a ∧ b
Законы рефлексивности
a v a = a a ∧ a =a
Закон отрицания отрицания (двойное отрицание)
¬ ¬ a = a
Свойства единицы и нуля
a v 0 = a a ∧ 1 =a
a v 1 = 1 a ∧ 0 =0
(a v b) ∧ (¬ a v b)= b (a ∧ b) v (¬ a ∧ b)= b
¬ 0=1 ¬ 1=0
Законы рефлексивности
a v a = a a ∧ a =a
Закон отрицания отрицания (двойное отрицание)
¬ ¬ a = a
Свойства единицы и нуля
a v 0 = a a ∧ 1 =a
a v 1 = 1 a ∧ 0 =0
(a v b) ∧ (¬ a v b)= b (a ∧ b) v (¬ a ∧ b)= b
¬ 0=1 ¬ 1=0
- Предыдущая
Фантомные боли Сумма
Сумма Площадь параллелограмма
Площадь параллелограмма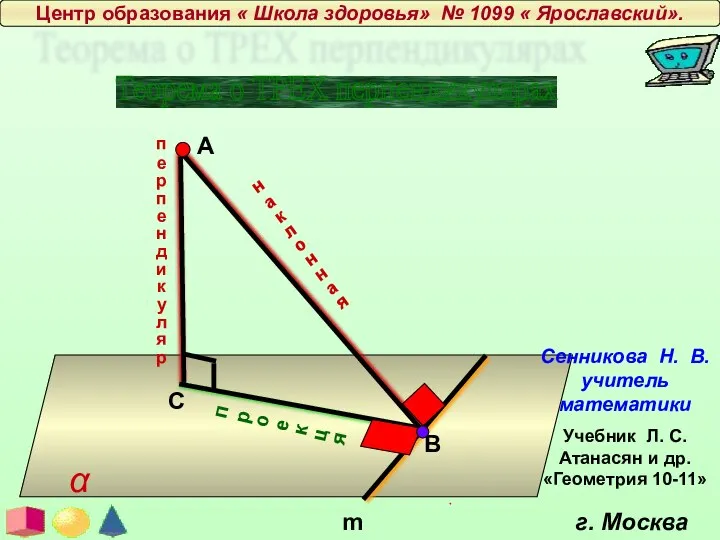 Теорема о трех перпендикулярах
Теорема о трех перпендикулярах Уравнения и неравенства
Уравнения и неравенства Дидактическая игра. Веселый ёжик
Дидактическая игра. Веселый ёжик Числа 6 и 7. Письмо цифры 6
Числа 6 и 7. Письмо цифры 6 Измерение углов
Измерение углов Состав чисел первого десятка
Состав чисел первого десятка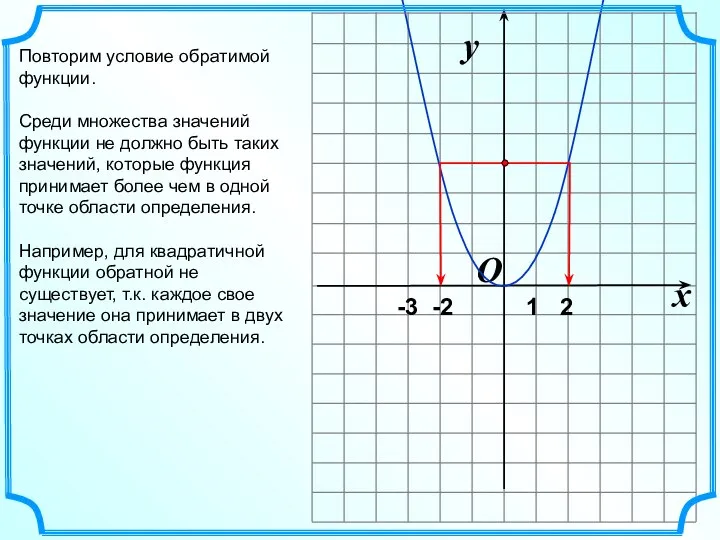 Арксинус
Арксинус Однородные тригонометрические уравнения
Однородные тригонометрические уравнения Пушкин и математика
Пушкин и математика Равенство векторов
Равенство векторов Относительные показатели: динамики, плана, координации
Относительные показатели: динамики, плана, координации Углы. Прямой и развернутый углы
Углы. Прямой и развернутый углы Алгоритм решения задач на нахождение слагаемых по сумме и разности
Алгоритм решения задач на нахождение слагаемых по сумме и разности Основное логарифмическое тождество
Основное логарифмическое тождество Разложение на множители разными способами
Разложение на множители разными способами Памятка по оформлению краткой записи к задачам
Памятка по оформлению краткой записи к задачам Процедуры и функции работы со строками
Процедуры и функции работы со строками Действия с десятичными дробями. Математические гонки
Действия с десятичными дробями. Математические гонки Определение стоимости проезда пассажира на железнодорожном транспорте. Задания
Определение стоимости проезда пассажира на железнодорожном транспорте. Задания Золотое сечение
Золотое сечение Модели решения функциональных и вычислительных задач. Методы и технологии моделирования
Модели решения функциональных и вычислительных задач. Методы и технологии моделирования Понятие треугольника
Понятие треугольника Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Углы
Углы Разложение многочлена на множители
Разложение многочлена на множители 54998861c58c436181d4716bc500367c
54998861c58c436181d4716bc500367c