Правильные многогранники

ЦОР "Правильные многогранники"
Позиция №1
Позиция № 5

Существует пять типов правильных выпуклых многогранников:
- правильный тетраэдр
- куб (гексаэдр)
- октаэдр (правильный восьмигранник)
- додекаэдр (правильный двенадцатигранник)
икосаэдр (правильный двадцатигранник)

Выпуклые правильные многогранники принято называть Платоновы тела.
Древнегреческий философ Платон (427 – 347 гг. до н.э.), который упомянул о правильных многогранниках в одной из своих работ, на самом деле не является первооткрывателем правильных выпуклых многогранников.
Они были известны задолго до Платона. При раскопках была найдена модель додекаэдра, служившая детской игрушкой более 2500 лет назад.
Доказательство
Правильных многогранников- 5

Тетраэдр
4
4
6
Куб
8
6
12
Октаэдр
6
8
12
Икосаэдр
12
20
30
Додекаэдр
20
12
30
2
2
2
2
2
В+Г-Р = 2
формула Эйлера
Исследование
Теорема Эйлера заложила фундамент нового раздела математики
— топологии.

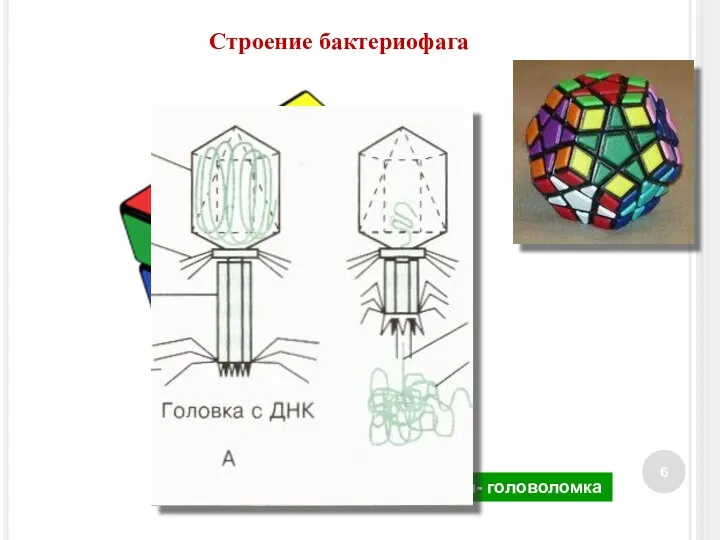
Кубик Рубика- головоломка
Строение бактериофага

Морис Эшер
Леонардо да Винчи «Тайная вечеря»
Сальвадор Дали

Согните и разогните каждую из полосок по линиям,
чтобы образовались сгибы.
2. Наложите синюю полоску на красную.
3. Сложите из красной тетраэдр.
4. Оберните синей полоской две грани красного тетраэдра
и оставшийся треугольник вставьте в щель между двумя
красными треугольниками
Практическая работа

ДОМАШНЕЕ ЗАДАНИЕ
1. Соберите без склеивания модель куба;
2. Продвинутый уровень- ответить на вопрос:
существуют ли кроме платоновых тел другие правильные многогранники (доказательство)?