Задачи на построение. 7 класс

Тест по теме «Окружность»
Выберите правильный вариант ответа.
1. Окружностью называется геометрическая фигура, которая а) состоит из точек плоскости, расположенных на данном расстоянии от данной точки плоскости;
б) состоит из всех точек плоскости, расположенных на данном расстоянии от данной точки плоскости.
2. Центром окружности является
а) точка, от которой одинаково удалены некоторые точки;
б) точка, от которой одинаково удалены все точки окружности.

Тест по теме «Окружность»
3. Радиусом окружности называется
а) отрезок, соединяющий любую точку окружности с центром;
б) отрезок, соединяющий любую точку окружности с центром окружности.
4. Хордой окружности называется
а) отрезок, соединяющий две любые точки окружности;
б) отрезок, соединяющий две любые точки.

Тест по теме «Окружность»
5. Диаметром окружности называется
а) прямая, проходящая через центр окружности;
б) хорда, проходящая через центр окружности.
Оцени себя.
Если у тебя 5 верных ответов – оценка 5;
4 верных ответа -- оценка 4;
3 верных ответа -- оценка 3.
Меньшее число верных ответов оценивается 2.

В геометрии выделяют задачи на построение, которые можно решить только с помощью двух инструментов: циркуля и линейки без масштабных делений.
Линейка позволяет провести произвольную
прямую, а также построить прямую, проходящую через две данные точки;
с помощью циркуля можно провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равным данному отрезку.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII

План решения задачи на построение.
Анализ ( нахождение связи между
элементами геометрической фигуры).
Построение с обязательным описанием хода его выполнения.
Доказательство получения искомой фигуры.
Исследование.

Набор инструментов

Набор инструментов

Ты узнаешь:
как построить угол, равный данному;
как построить биссектрису данного угла;
как разделить отрезок пополам.
Ты научишься:
решать задачи на построение угла, равного данному, на построение биссектрисы, на деление отрезка пополам.

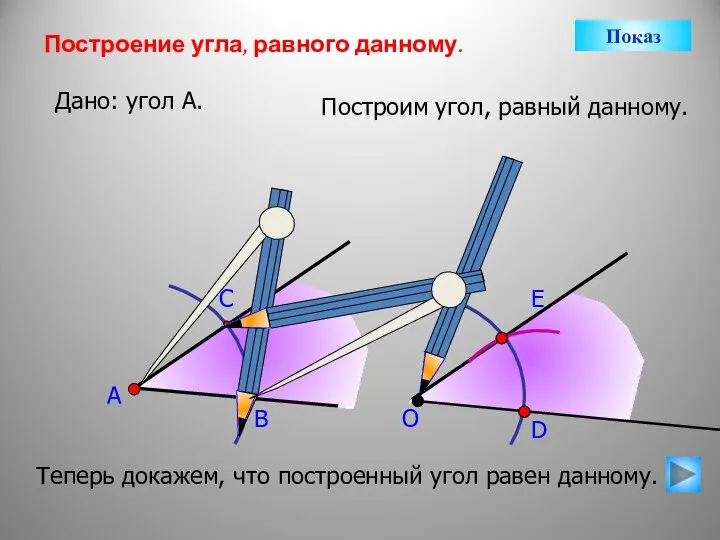
А
В
С
Построение угла, равного данному.
Дано: угол А.
Построим угол, равный данному.
О
D
E
Теперь докажем, что построенный угол равен данному.
Показ

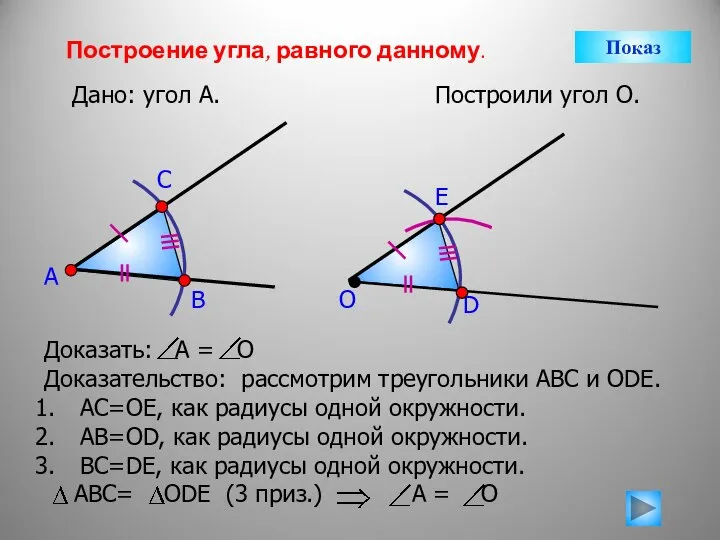
Построение угла, равного данному.
Дано: угол А.
А
Построили угол О.
В
С
О
D
E
Доказать: А = О
Доказательство: рассмотрим треугольники АВС и ОDE.
АС=ОЕ, как радиусы одной окружности.
АВ=ОD, как радиусы одной окружности.
ВС=DE, как радиусы одной окружности.
АВС= ОDЕ (3 приз.) А = О
Показ

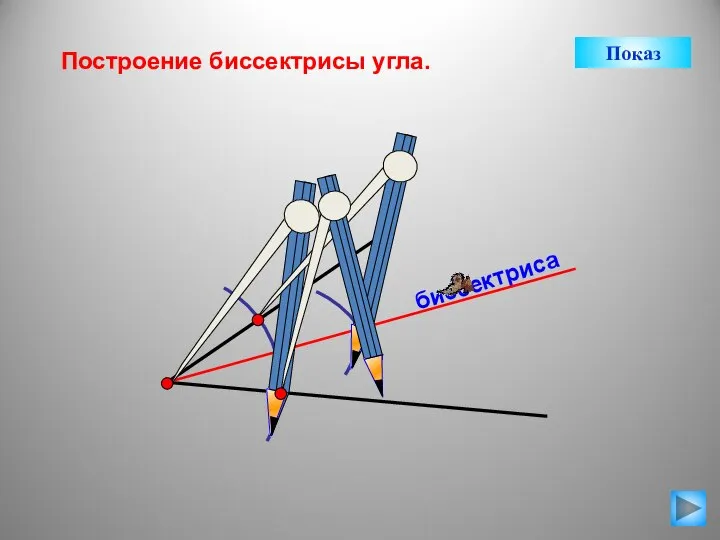
биссектриса
Построение биссектрисы угла.
Показ

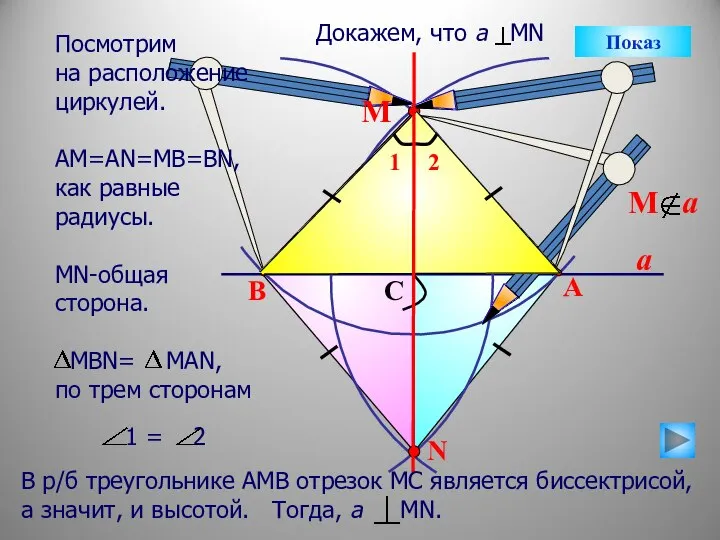
a
N
B
A
C
М
Показ
Посмотрим
на расположение
циркулей.
АМ=АN=MB=BN,
как равные радиусы.
МN-общая сторона.
MВN= MAN,
по трем сторонам

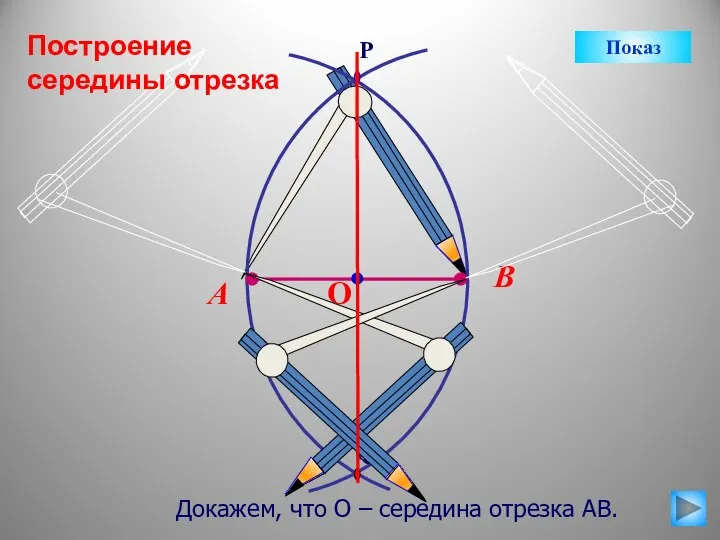
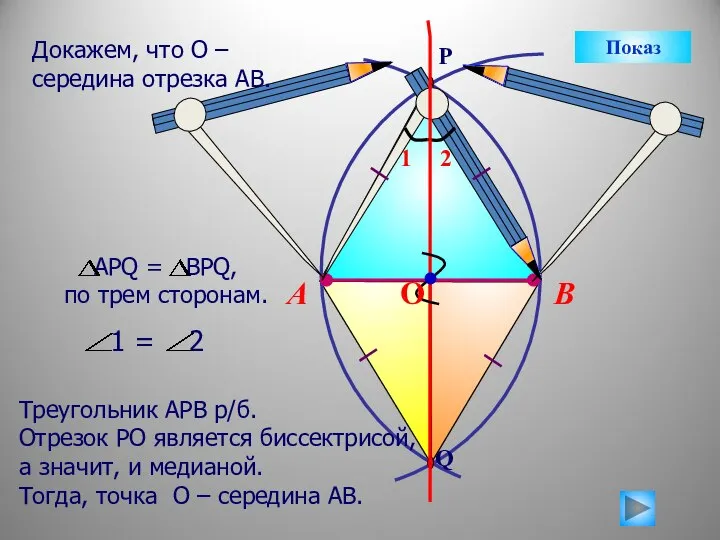
Докажем, что О – середина отрезка АВ.
Показ
Построение
середины отрезка

В
А
Треугольник АРВ р/б.
Отрезок РО является биссектрисой,
а значит, и медианой.
Тогда, точка О – середина АВ.
Показ
Докажем, что О –
середина отрезка АВ.

Задание 1

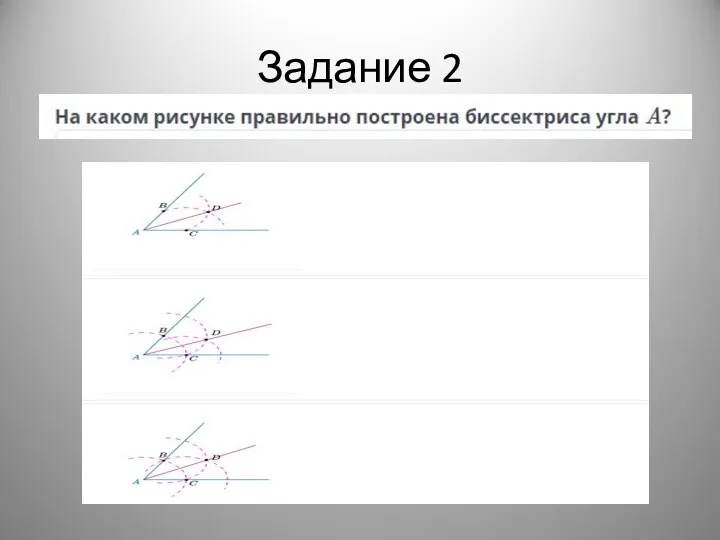
Задание 2

Задание 3

Задание 4

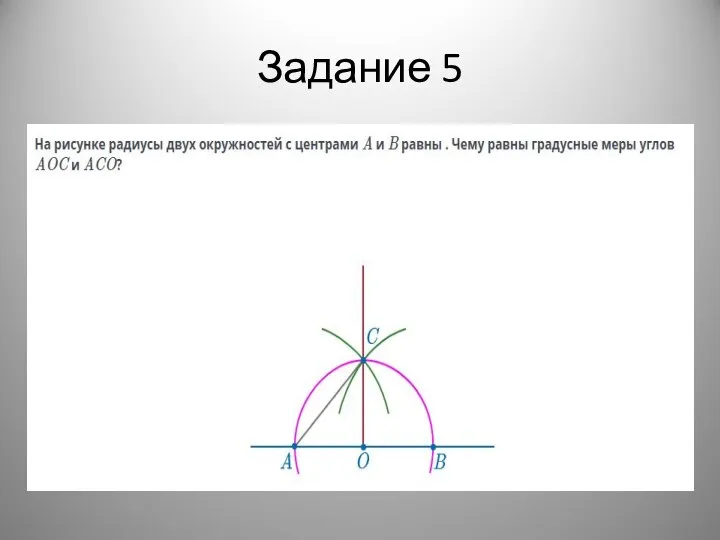
Задание 5

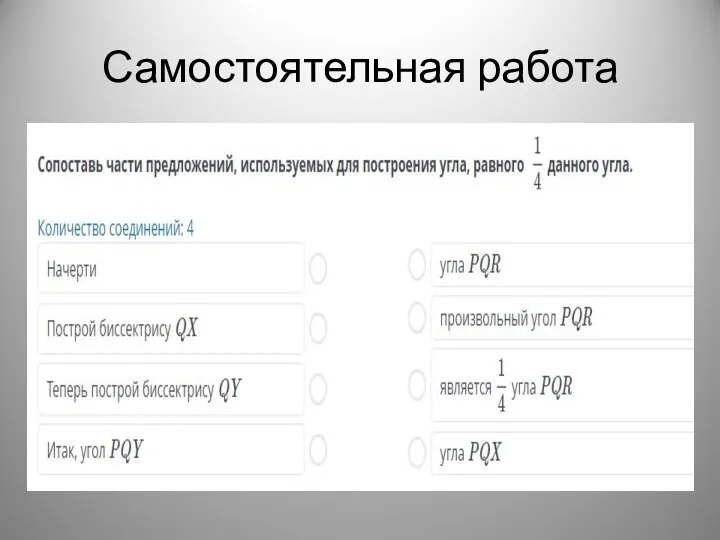
Самостоятельная работа

Учебные задания