Интервальные оценки

Исходной информацией является серия измерений неизвестной величины А:
x1, x2, … xn (1)
Проблема № 1: получить численное значение определенной физической величины А экспериментальными методами.
В математической статистике серия измерений рассматривается как выборка из генеральной совокупности.
Согласно постулату 2, измеряемая величина А совпадает с генеральным средним MG

Генеральная совокупность является бесконечным множеством значений, характеризуемое распределением вероятностей.
Существуют дискретные и непрерывные генеральные совокупности.
Генеральная совокупность обладает числовыми характеристиками, важнейшие из которых:
генеральное среднее MG
генеральная дисперсия DG

Точечные оценки измеряемой величины
(2)
Среднее статистическое
Выборочная медиана m*

Состоятельной, несмещенной и эффективной оценкой генерального среднего MG нормальной генеральной совокупности является среднее статистическое.
Дисперсия среднего статистического равна DG /n

наилучшая оценка среднеквадратичного отклонения среднего статистического
Можно ли записать результат измерений в виде :
???

где η − доверительная вероятность.
Доверительный интервал для измеряемой величины А
(для генерального среднего)
(3)
Величина доверительной вероятности выбирается на основе принципа практической достоверности
t – пока неизвестное число

Уравнение (3) означает, что две случайные величины
с вероятностью η ограничивают постоянную, но неизвестную величину MG = A.
безразмерное число t −
коэффициент Стьюдента.

Случайное события
и
эквивалентны

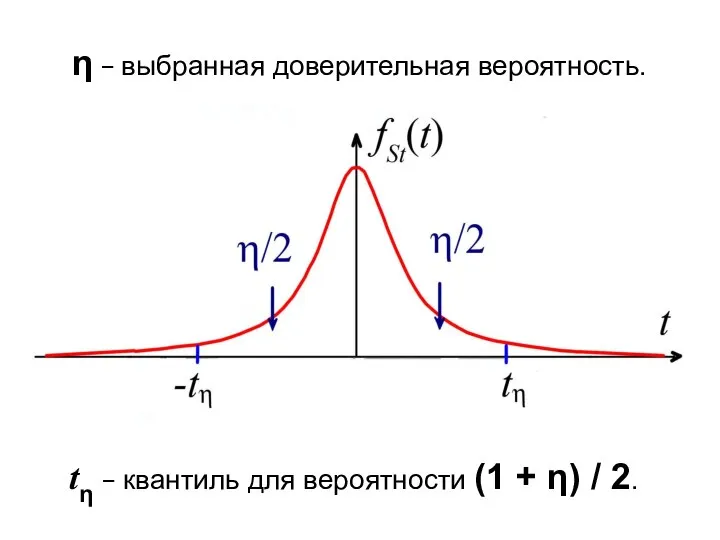
Это означает, что случайная величина
с вероятностью η попадает в интервал, ограниченный числами −t и t .

В теории вероятностей доказано, что если генеральная совокупность нормальная (гауссова), то случайная величина
имеет распределение Стьюдента с числом степеней свободы ν = n – 1.

Следовательно, числа ± t представляют собой симметричные пределы интегрирования плотности распределения Стьюдента, соответствующие вероятности η.
где fSt – функция плотности случайной величины с распределением Стьюдента.

η − выбранная доверительная вероятность.
tη − квантиль для вероятности (1 + η) / 2.

По данной выборке вычисляются среднее статистическое и несмещенная оценка дисперсии s2.
По заданной доверительной вероятности η и числу степеней свободы ν = n – 1 извлекается из таблицы значение коэффициента Стьюдента tν ,η .
Рассчитываются границы доверительного интервала:
Процедура построения доверительного интервала для измеряемой величины.

Доверительный интервал для генеральной дисперсии
Если генеральная совокупность имеет нормальное (гауссово) распределение, то случайная величина
имеет распределение вероятностей «хи-квадрат» с ν = n – 1 степенями свободы
DG – генеральная дисперсия, n - объем выборки

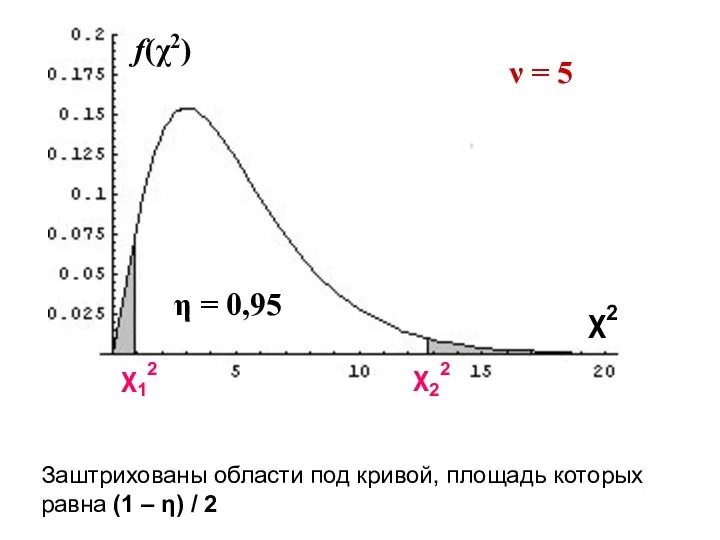
Определим числа χ12 и χ22 следующими уравнениями для вероятностей событий
(12)
(13)

Согласно уравнению (12), вероятность того, что значение случайной величины χν2 не превысит числа χ12, равна (1 – η ) / 2.
Согласно уравнению (13), вероятность того, что значение той же случайной величины χν2 превышает число χ22 , равна также (1 – η ) / 2.

Заштрихованы области под кривой, площадь которых равна (1 – η) / 2
χ12
χ22
χ2
f(χ2)
ν = 5
η = 0,95

Вероятностное уравнение, эквивалентное уравнениям (12) и (13) имеет вид :
χ12 − квантиль для вероятности (1 - η) / 2.,
χ22 − квантиль для вероятности (1 + η) / 2.

Иначе говоря, доверительной вероятности η соответствует следующий доверительный интервал для генеральной дисперсии
Величины χ12 и χ22 извлекаются из таблиц квантилей случайной величины «хи-квадрат», составленными для различных доверительных вероятностей η и определённых чисел степеней свободы ν.
(14)

Наилучшей оценкой генеральной дисперсии является
где