Содержание
- 2. Занятие №1. Основным методом решения иррациональных неравенств является метод сведения исходного неравенства к равносильной системе рациональных
- 3. Поэтому данное неравенство равносильно следующей системе неравенств. 1.Рассмотрим иррациональное неравенство вида Решение. ОДЗ неизвестного будет определяться
- 4. Пример 1. Решить неравенство
- 5. Пример 1. Решить неравенство
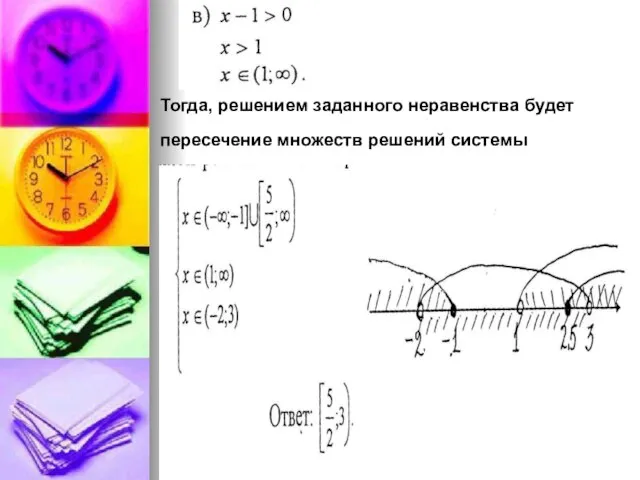
- 6. Тогда, решением заданного неравенства будет пересечение множеств решений системы
- 7. 2.Рассмотрим неравенство вида: Решение. ОДЗ неизвестного будет определяться из условия Но, в отличие от предыдущего, (x)
- 8. В случае же Заданное неравенство равносильно следующей системе неравенств: Тогда, из последней системы видно, что первое
- 9. Пример 2. Решить неравенство
- 10. Пример 2. Решить неравенство: Рассмотрим два случая:
- 11. Занятие №2 Цель: Рассмотреть неравенства вида: При решении иррациональных неравенств используются те же методы, что и
- 12. 1.Неравенство вида равносильно системе неравенств: 2.Неравенство вида равносильно неравенству f(x)
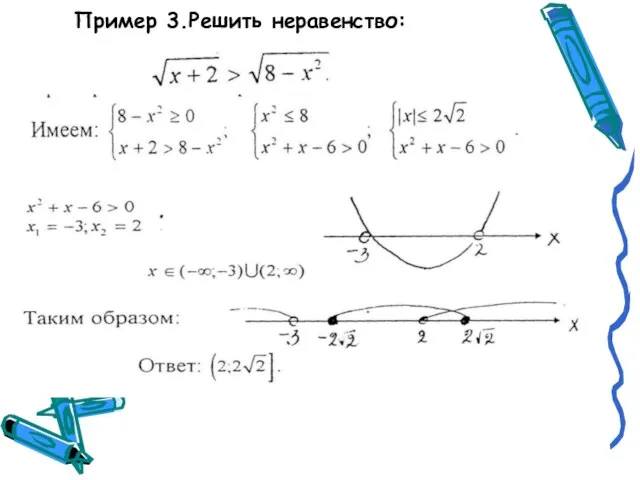
- 13. Пример 3. Решить неравенство
- 14. Пример 3.Решить неравенство:
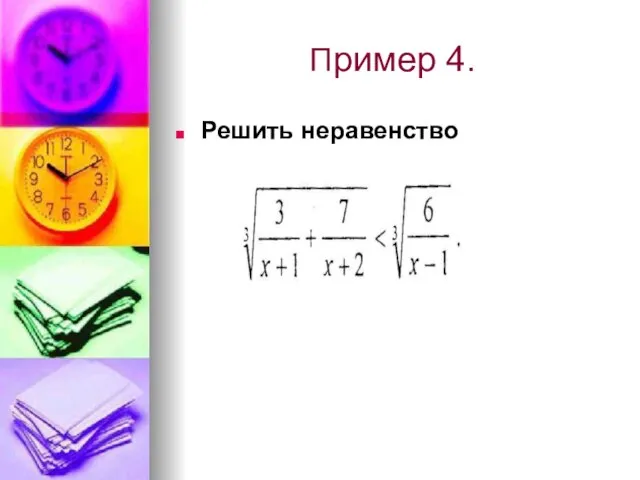
- 15. Пример 4. Решить неравенство
- 16. Пример4.Решить неравенство:
- 17. Занятие №3. Цель: Рассмотреть решения неравенств методом интервалов. При решении иррациональных неравенств методом интервалов надо всегда
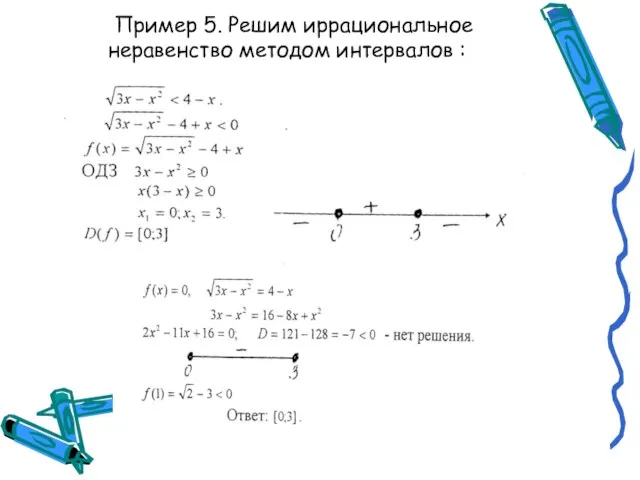
- 18. Пример 5. Решим иррациональное неравенство методом интервалов :
- 19. Занятие №4. Цель: Рассмотреть решения иррациональных неравенств введением новой переменной
- 20. Пример 6. Решим неравенство введением новой переменной
- 21. ешим неравенствопеременно
- 22. Занятие №5. Цель: Рассмотреть решения иррациональных неравенств методом замены множителя .
- 23. Пример №7. Решим неравенство методом замены множителя
- 24. Домашнее задание. Решить неравенство: Пример 1. Пример 3. Пример 2. Пример 4. Пример 5.
- 25. ВЫВОДЫ: Основным методом решения иррациональных неравенств является метод сведения исходного неравенства к равносильной системе рациональных неравенств
- 27. Скачать презентацию




















 Прямоугольный параллелепипед
Прямоугольный параллелепипед Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений Множества и отображения
Множества и отображения Последовательности
Последовательности Презентация на тему Загадочное число Пи
Презентация на тему Загадочное число Пи  Презентация на тему Прямоугольные треугольники
Презентация на тему Прямоугольные треугольники  Формулы куба суммы и куба разности двух выражений
Формулы куба суммы и куба разности двух выражений Расчёт радиатора для транзистора
Расчёт радиатора для транзистора Простейшие функции. Операция суперпозиции
Простейшие функции. Операция суперпозиции Решение задач по теме: Параллелограмм (1)
Решение задач по теме: Параллелограмм (1) Азбука
Азбука Решение линейных уравнений с одной переменной
Решение линейных уравнений с одной переменной Занимательная геометрия
Занимательная геометрия Метод решения систем линейных уравнений методом Крамера
Метод решения систем линейных уравнений методом Крамера Системы линейных неравенств с одной переменной. Решение системы линейных неравенств с одной переменной
Системы линейных неравенств с одной переменной. Решение системы линейных неравенств с одной переменной Решение уравнений и построение точек по их координатам. 6 класс
Решение уравнений и построение точек по их координатам. 6 класс Решение задач на нахождение значений двух величин по сумме и разности
Решение задач на нахождение значений двух величин по сумме и разности Презентация на тему Формулы приведения
Презентация на тему Формулы приведения  Параллель к перпендикуляру
Параллель к перпендикуляру Презентация
Презентация Алгоритмы на графах
Алгоритмы на графах Путь и перемещение
Путь и перемещение Глубина озера. Теорема Пифагора
Глубина озера. Теорема Пифагора Интервальное оценивание параметров распределения
Интервальное оценивание параметров распределения Тригонометрия в жизни
Тригонометрия в жизни Сравнительный анализ лирики А.С. Пушкина и В.В. Маяковского методами математической статистики
Сравнительный анализ лирики А.С. Пушкина и В.В. Маяковского методами математической статистики Вычислительная математика. Вычисление серии интегралов. Вычисление корней квадратного уравнения. Вычисление exp(x)
Вычислительная математика. Вычисление серии интегралов. Вычисление корней квадратного уравнения. Вычисление exp(x) Сфера и плоскость
Сфера и плоскость