Содержание
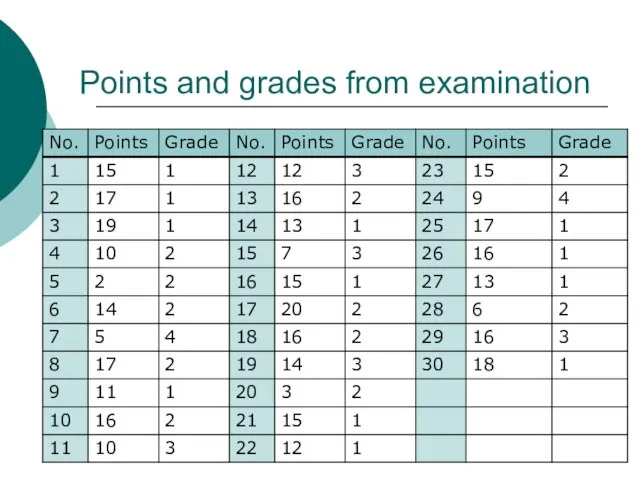
- 2. Points and grades from examination
- 3. Sample size n=30 Data sorting → Frequency table both for quantitative and qualitative data
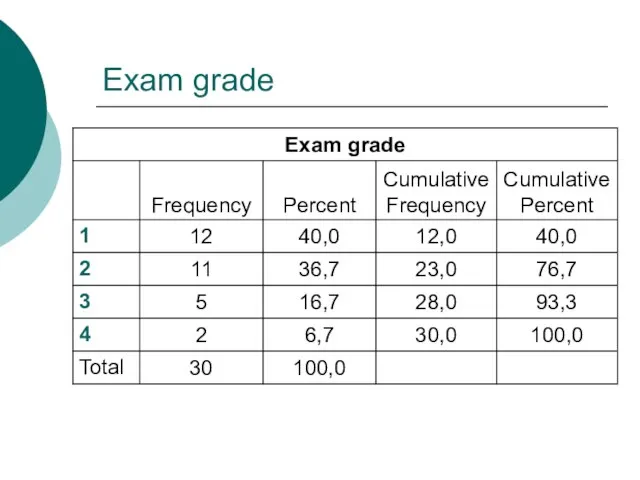
- 4. Exam grade
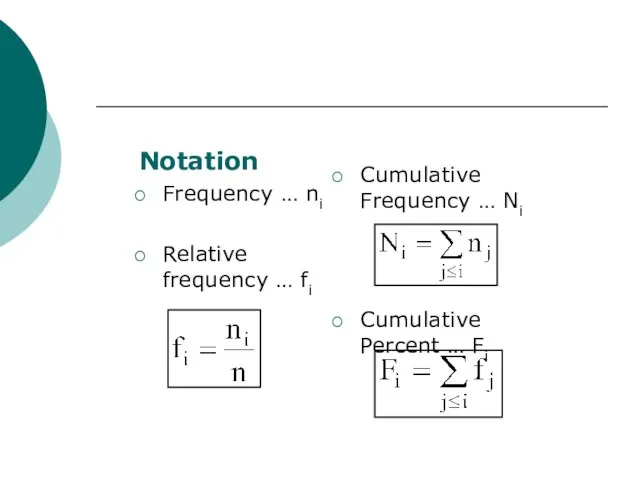
- 5. Notation Frequency … ni Relative frequency … fi Cumulative Frequency … Ni Cumulative Percent … Fi
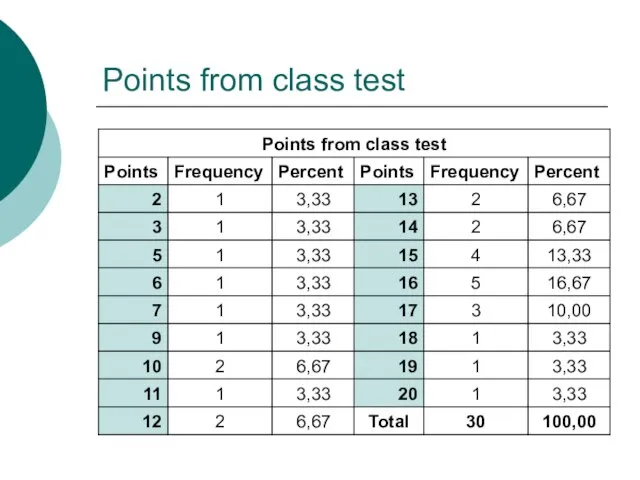
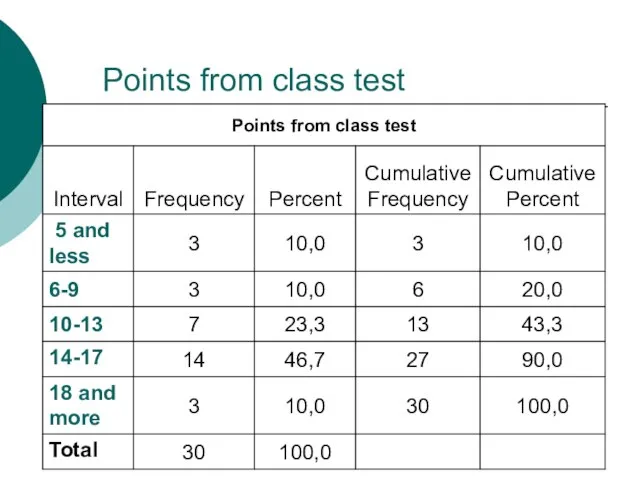
- 6. Points from class test
- 7. Quantitative variables Grouping into class intervals
- 8. How to select the intervals Number of intervals → in order to describe the characteristics of
- 9. …then h … width of interval R … Range=xmax-xmin k … number of intervals Our example:
- 10. Points from class test
- 11. Measures of Central Tendency Measures that represent with a proper value the tendency of most data
- 12. The arithmetic mean Notation arithmetic mean …… the sum of the values of a variable divided
- 13. Properties of the arithmetic mean it is expressed in the same unit of measure as the
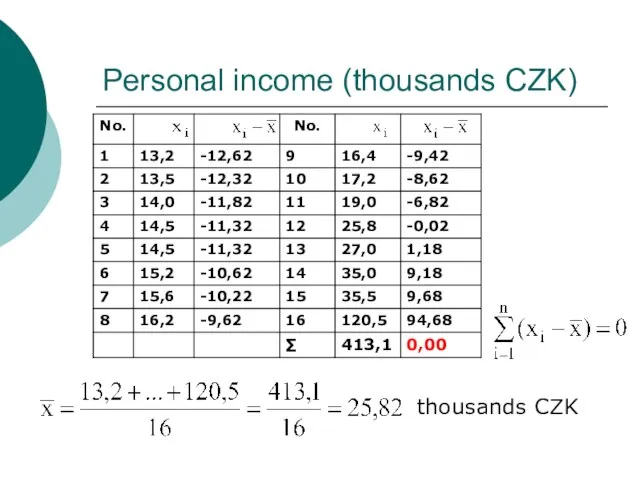
- 14. Personal income (thousands CZK) thousands CZK
- 15. 12 of 16 values are below the arithmetic mean, because of the highest value x16=120,5 (directors
- 16. Other measures of central tendency The median…. The value above and below which one-half of the
- 17. Other measures of central tendency The mode…. The value that occurs with greatest frequency for qualitative
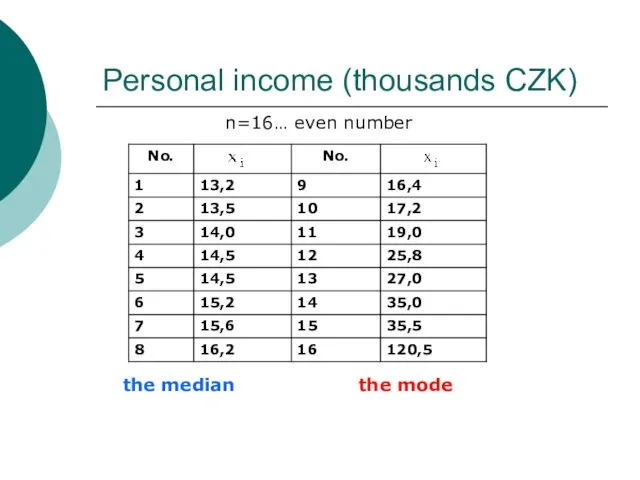
- 18. Personal income (thousands CZK) n=16… even number the median the mode
- 19. Personal income (thousands CZK) n=16… even number the median the mode
- 20. Use of mean, median and mode The arithmetic mean member of mathematical system in advanced statistical
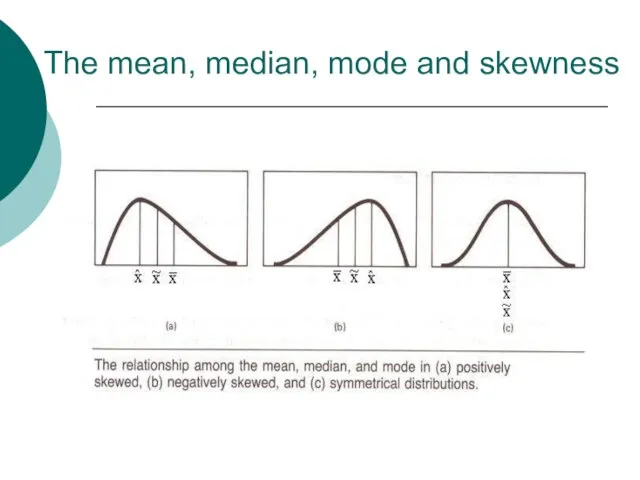
- 21. The mean, median, mode and skewness
- 22. to describe the spread of the data, its variation around a central value we want to
- 24. The Range….R it is the distance between the largest and the smallest value R=xmax-xmin it does
- 25. The Variance…s2 it is an average squared deviation of each value from the mean it is
- 26. Working formulas For easier computation Formula 1 Formula 2
- 27. the variance explains both the variability of the values around the arithmetic mean the variability among
- 28. The Standard Deviation…s it is the square root of variance when computing the variation based on
- 29. it is expressed in the same unit of measure as the observed variable the size of
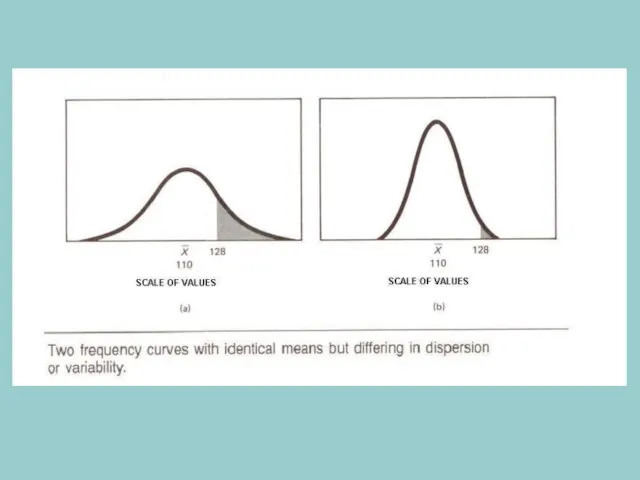
- 30. Two data sets with the same arithmetic mean and different SD
- 31. Example – Personal income (thousands CZK) thousands CZK
- 32. Coefficient of Variation…V the ratio of the standard deviation to the mean often reported as a
- 33. it is a relative measure of dispersion used when comparing two data sets with different units
- 34. Example – Personal income (thousands CZK)
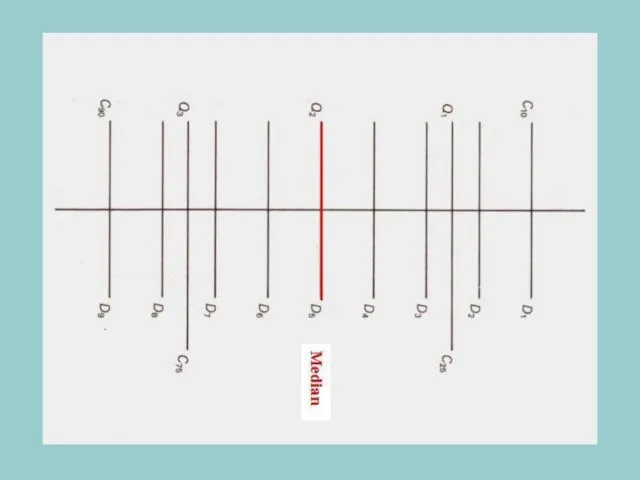
- 35. Percentiles (Centiles) value below which a certain percent of observations fall scale of percentile ranks is
- 36. Deciles divides a distribution into 10 equal parts there are 9 deciles D1 – 1st decile
- 37. divides a distribution into 4 equal parts Q1 - 25 percent of values fall below it
- 39. Graphing Techniques
- 40. Constructing graphs – Bar graph x – axis: labels of categories y – axis: frequency (relative
- 41. Arranging the graph nominal variables – we can arrange the categories in any order:alphabetically, decreasing/increasing order
- 45. Constructing graphs – Pie graph Pie chart – a circle divided into sectors each sector represents
- 47. Constructing graphs – Histogram bar graph for quantitative data values are grouped into intervals (classes) constructed
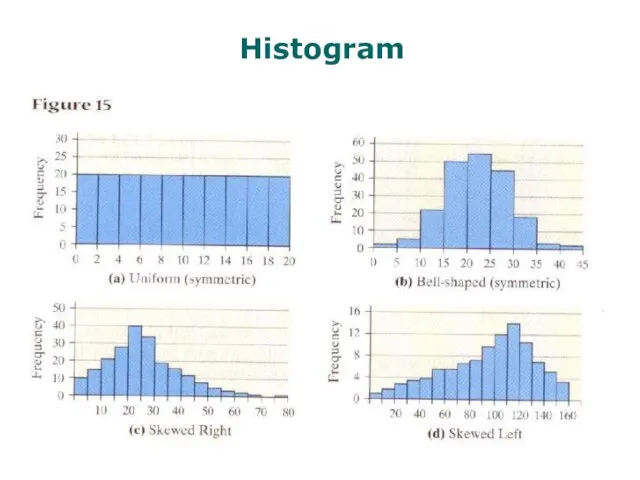
- 49. Histogram
- 51. Constructing graphs – Boxplot box-and-whisker diagram five number summary
- 52. Boxplot Q3 Q1 Q2
- 55. Скачать презентацию


































 Логарифмы вокруг нас
Логарифмы вокруг нас Решение простейших тригонометрических уравнений с помощью числовой окружности
Решение простейших тригонометрических уравнений с помощью числовой окружности Деление десятичных дробей
Деление десятичных дробей Возведение в степень
Возведение в степень Obratnye_trigonometricheskie_funktsii (1)
Obratnye_trigonometricheskie_funktsii (1) Экологическое воспитание через урок математики Учитель начальных классов Зайцева Вероника Петровна
Экологическое воспитание через урок математики Учитель начальных классов Зайцева Вероника Петровна Числовые выражения
Числовые выражения Презентация на тему В гостях у Маши (5 класс)
Презентация на тему В гостях у Маши (5 класс)  Работу выполнила: Ученица 5б класса Беляева Александра Учитель: Сахокия Д.А.
Работу выполнила: Ученица 5б класса Беляева Александра Учитель: Сахокия Д.А. Понятие вектора
Понятие вектора Таблица сложения
Таблица сложения Обыкновенная дробь
Обыкновенная дробь Числовые неравенства
Числовые неравенства Логические головоломки
Логические головоломки Прием письменного вычитания в случаях вида 50-24. Урок математики во 2 классе. (По УМК «Начальная школа XXI век.»)
Прием письменного вычитания в случаях вида 50-24. Урок математики во 2 классе. (По УМК «Начальная школа XXI век.») Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Разложение многочлена на множители
Разложение многочлена на множители Презентация на тему Простые числа
Презентация на тему Простые числа  Параллельные прямые в архитектуре
Параллельные прямые в архитектуре Сфера и шар
Сфера и шар Умножение натуральных чисел
Умножение натуральных чисел Metode numerice – pregătire
Metode numerice – pregătire Оригами. Проект по математике
Оригами. Проект по математике Решение неравенств с одной переменной
Решение неравенств с одной переменной Выделение в число общего количества единиц любого разряда
Выделение в число общего количества единиц любого разряда Методы измерений в квалиметрии
Методы измерений в квалиметрии Несобственные интегралы первого рода
Несобственные интегралы первого рода Формулы изменившие мир
Формулы изменившие мир