Исследование функции на монотонность и экстремумы

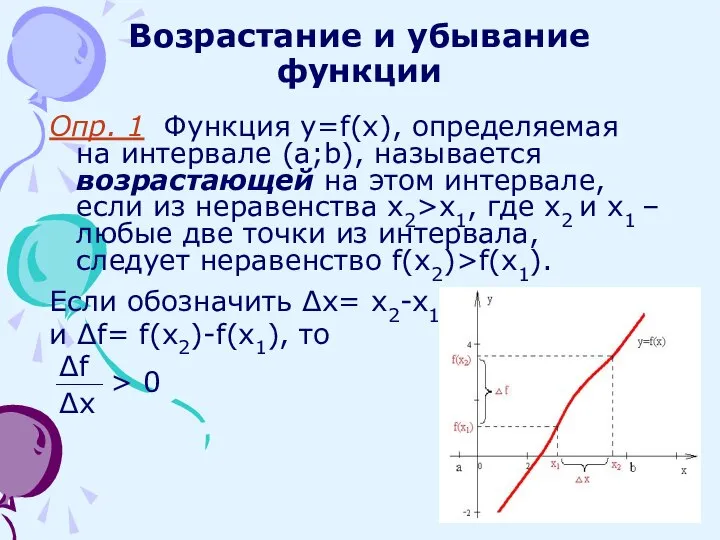
Возрастание и убывание функции
Опр. 1 Функция y=f(x), определяемая на интервале (a;b), называется возрастающей на этом интервале, если из неравенства x2>x1, где x2 и x1 – любые две точки из интервала, следует неравенство f(x2)>f(x1).
Если обозначить Δx= x2-x1
и Δf= f(x2)-f(x1), то
Δf
____ > 0
Δx

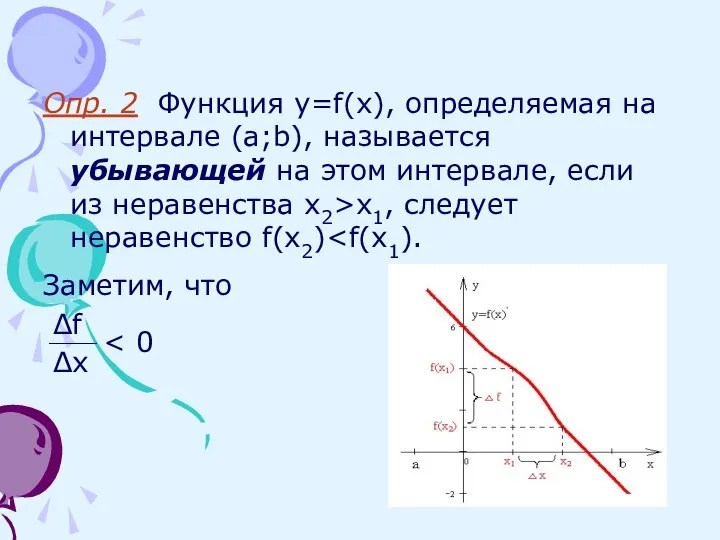
Опр. 2 Функция y=f(x), определяемая на интервале (a;b), называется убывающей на этом интервале, если из неравенства x2>x1, следует неравенство f(x2)
Заметим, что
Δf
____ < 0
Δx

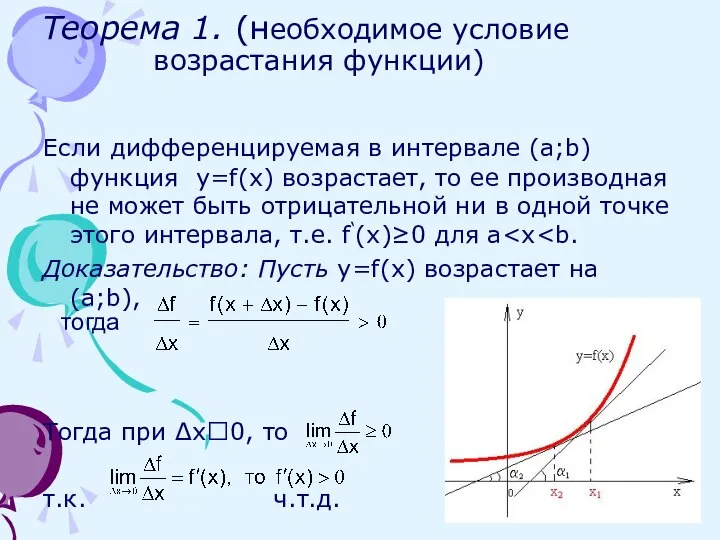
Теорема 1. (необходимое условие возрастания функции)
Если дифференцируемая в интервале (a;b) функция y=f(x) возрастает, то ее производная не может быть отрицательной ни в одной точке этого интервала, т.е. f‘(x)≥0 для a
Доказательство: Пусть y=f(x) возрастает на (a;b),
Тогда при Δx?0, то
т.к. ч.т.д.
тогда

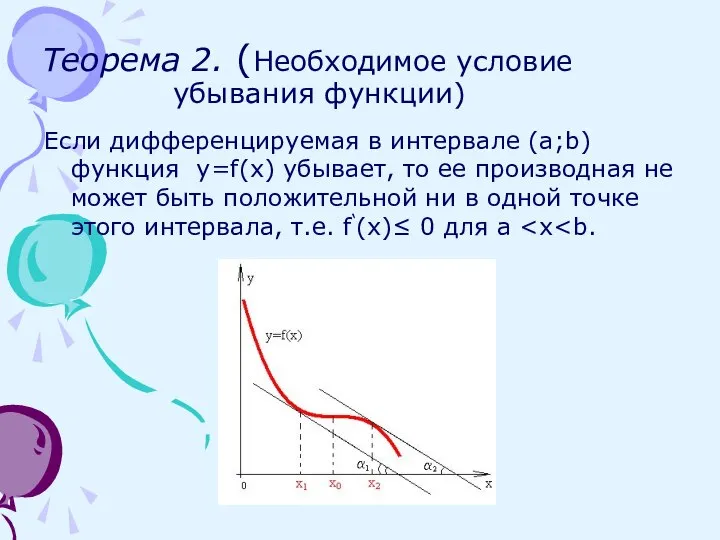
Теорема 2. (Необходимое условие убывания функции)
Если дифференцируемая в интервале (a;b) функция y=f(x) убывает, то ее производная не может быть положительной ни в одной точке этого интервала, т.е. f‘(x)≤ 0 для a

Теорема 3. (Достаточное условие возрастания функции)
Если непрерывная на [a;b] функция y=f(x) в каждой внутренней точке имеет положительную производную, то функция возрастает на [a;b]
Доказательство: Пусть y=f'(x) для всех a
x1 из [a;b].
По теореме Лагранжа f(x2)-f(x1)=(x2-x1) f'(с), где x1≤с
поэтому по условию f'(с)>0
и x2 -x1 >0 имеем f(x2)-f(x1)>0, т.е. из x2>x1 следует
f(x2) >f(x1), т. е. функция возрастает, ч.т.д.

Теорема 4. (Достаточное условие убывания функции)
Если непрерывная на [a;b] функция y=f(x) в каждой внутренней точке имеет отрицательную производную, то функция убывает на [a;b].
Пример 1. Найти интервал монотонности функции y=x3-3x.
Решение. Находим область определения функции D(y)=R

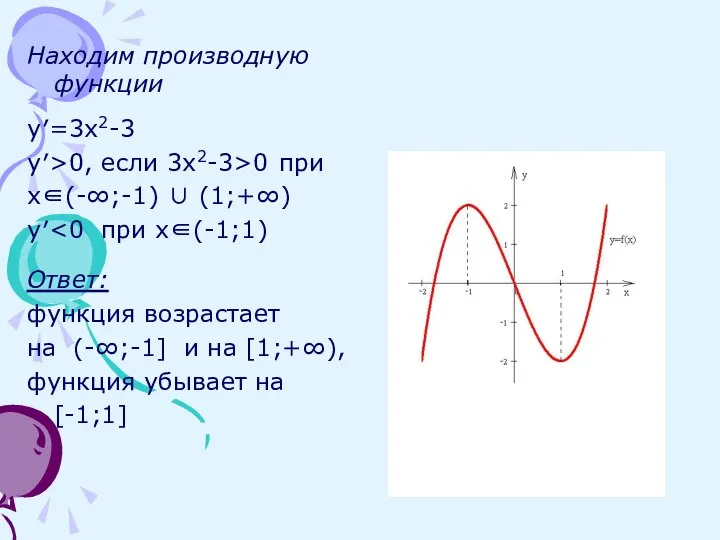
Находим производную функции
y′=3x2-3
y′>0, если 3x2-3>0 при
x∈(-∞;-1) ∪ (1;+∞)
y′<0 при x∈(-1;1)
Ответ:
функция возрастает
на (-∞;-1] и на [1;+∞),
функция убывает на [-1;1]

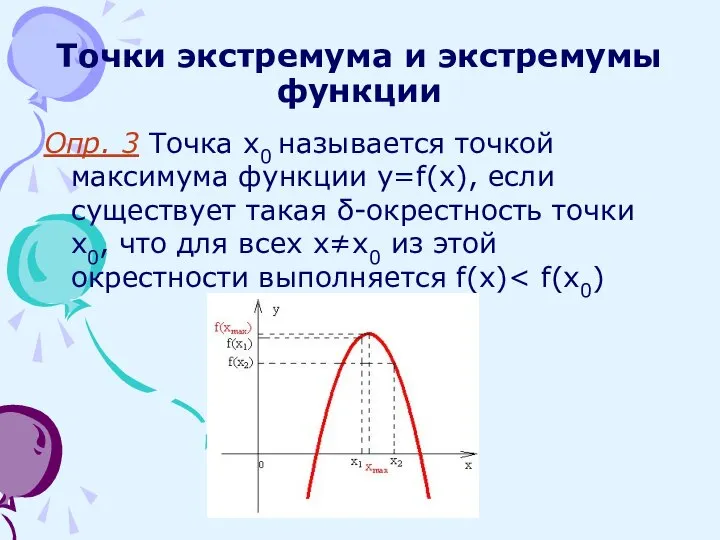
Точки экстремума и экстремумы функции
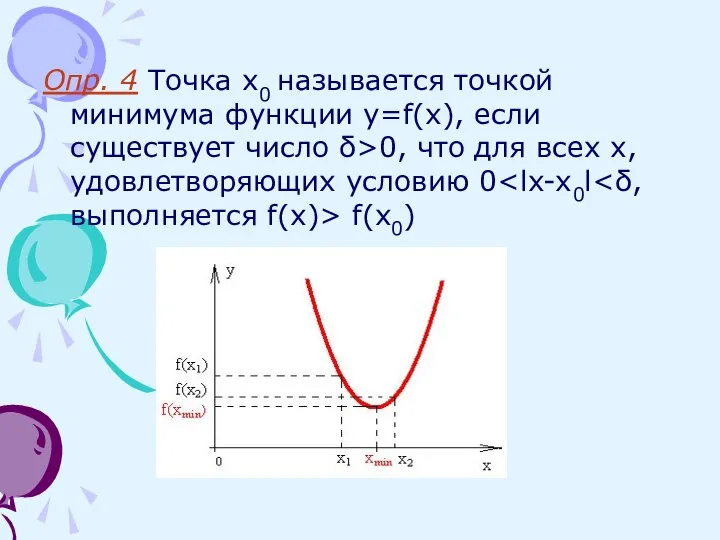
Опр. 3 Точка x0 называется точкой максимума функции y=f(x), если существует такая δ-окрестность точки x0, что для всех x≠x0 из этой окрестности выполняется f(x)< f(x0)

Опр. 4 Точка x0 называется точкой минимума функции y=f(x), если существует число δ>0, что для всех х,удовлетворяющих условию 0
f(x0)

Точка максимума и точка минимума называются точками экстремума.
Значение функции в точках экстремума называется экстремумом функции, т.е.
fmax=f(xmax) – максимум функции
fmin=f(xmin) – минимум функции.

Теорема 5. (Необходимое условие экстремума)
Если дифференциальная функция y=f(x) имеет экстремум в точке x0, то ее производная в этой точке равна 0, т.е. f′(x0) =0.
Доказательство: Пусть x0 – точка максимума, тогда в окрестности точки x0 выполняется f(x0)>f(x), поэтому
и
По условию существует производная, которая равна
Имеем: f’(x0)≤0 при Δx>0 и f’(x0)≥0 при Δx<0, следовательно f′(x0) =0, ч.т.д.

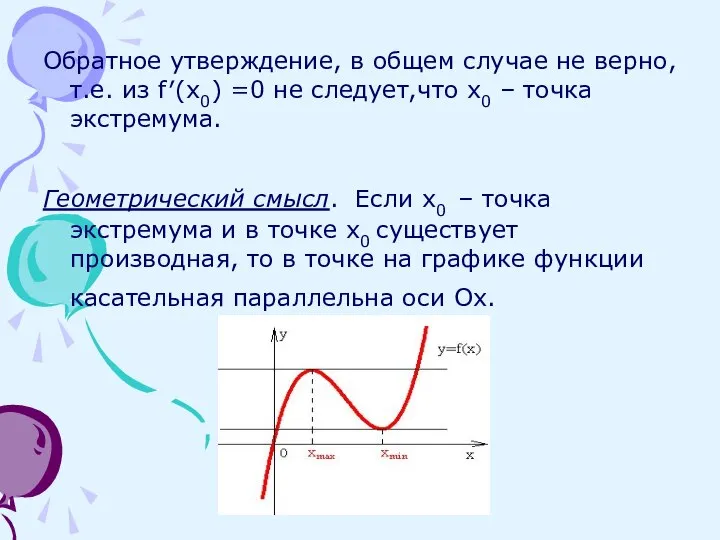
Обратное утверждение, в общем случае не верно, т.е. из f′(x0) =0 не следует,что x0 – точка экстремума.
Геометрический смысл. Если x0 – точка экстремума и в точке x0 существует производная, то в точке на графике функции касательная параллельна оси Оx.

Теорема 6. (Достаточное условие экстремума)
Если непрерывная функция y=f(x) дифференцируема в δ-окружности критической точки х0 и при переходе через нее (слева направо) f′(x) меняет знак, то х0 – точка экстремума, причем,
если с «+» на «-», то х0 – точка максимума,
с «-» на «+», то х0 – точка минимума.
Доказательство: Рассмотрим δ-окр-сть точки х0. Пусть f′(x) >0 при любых х ∈(х0 - δ;х0) и f′(x)<0 при любых х∈(х0; х0 + δ). Тогда функция f(x) возрастает на (х0 - δ; х0) и убывает на (х0; х0 + δ), следовательно f(x0) – наибольшее значение на
(х0 - δ; х0 + δ), т.е. f(x) < f(x0) для х ∈ (х0 - δ; х0) ∪ (х0; х0 + δ), следовательно точка х0 – точка максимума функции, ч.т.д.

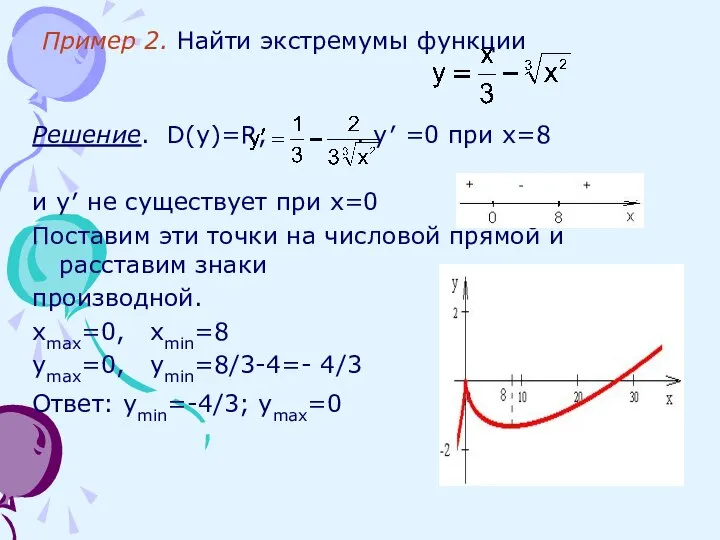
Пример 2. Найти экстремумы функции
Решение. D(y)=R, . y′ =0 при х=8
и y′ не существует при х=0
Поставим эти точки на числовой прямой и расставим знаки
производной.
xmax=0, xmin=8
ymax=0, ymin=8/3-4=- 4/3
Ответ: уmin=-4/3; ymax=0

Теорема 7. (Достаточное условие экстремума,если существует y′′)
Если в точке х0 существует f′(x) и f′(x0)=0, а вторая производная не равна 0,т.е. f′′(x0)≠ 0, то при f′′(x0)< 0 в точке x0 функция имеет максимум, а при f′′(x0)> 0 в точке x0 функция имеет минимум.

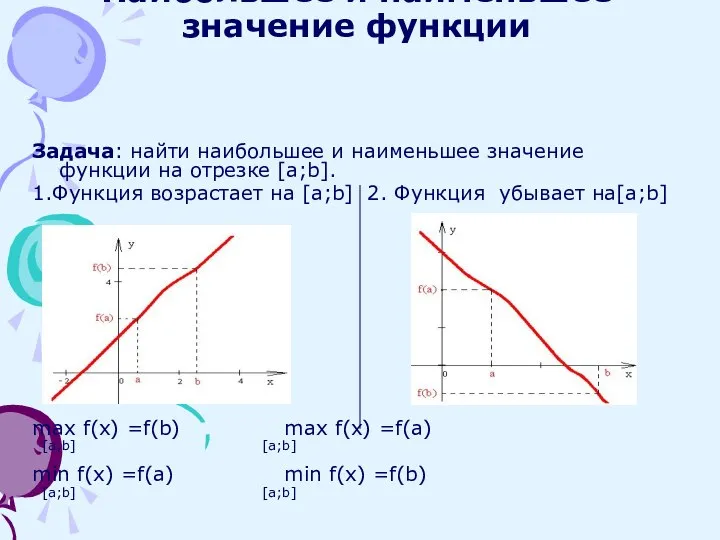
Наибольшее и наименьшее
значение функции
Задача: найти наибольшее и наименьшее значение функции на отрезке [a;b].
1.Функция возрастает на [a;b] 2. Функция убывает на[a;b]
max f(x) =f(b) max f(x) =f(a)
[a;b] [a;b]
min f(x) =f(a) min f(x) =f(b)
[a;b] [a;b]

3. Функция немонотонна на [a;b]
max f(x) =f(b)
[a;b]
min f(x) =fmin [a;b]

Алгоритм нахождения наибольшего и наименьшего значения функции y=f(x) на отрезке [a;b].
Найти f(a)=A и f(b)=B.
Найти нули производной и точки, в которых производная не существует.
Если найденные точки принадлежат [a;b], то найти значения функции в этих точках.
Выбрать из всех найденных значений функции наибольшее и наименьшее.

Пример 3. Найти наибольшее и наименьшее значение функции f(x)=3x4+4x3+1 на [-2;1]
Решение: 1.f(-2)=3·16+4·(-8)+1=48-32+1=17,
f(1)=3+4+1=8.
2.Находим производную функции f′(x)=12x3+12x2
f′(x)=0 при x=0 ∈ [-2;1], х=-1Є[-2;1].
3. f(0)=1, f(-1)=3-4+1=0.
4. Сравниваем найденные значения функции,
имеем 0<1<8<17.
Ответ: ;

ПРИМЕНЕНИЕ
Решением задач на нахождение наибольшего и наименьшего значения занимается линейное программирование.
Задачи: транспортная задача о перевозке груза с минимальными затратами;
Задача об организации производственного процесса с целью получения максимальной прибыли.