Слайд 2Корреляция – это зависимость между двумя случайными величинами.
Корреляция
Между различными явлениями существуют

сложные и многообразные связи. Их можно классифицировать.
В технике и естествознании часто говорят о функциональной зависимости. Например скорость выведения лекарственного вещества из организма.
Однако, многие явления происходят при воздействии многочисленных факторов, в этом случае, связь теряет свою строгую функциональность.
В результате, одна случайная переменная реагирует на изменения другой переменой изменением своего закона распределения.
Слайд 3Изучение статистических зависимостей основывается на исследовании таких связей между случайными переменными, при

которых значение одной изменяется в зависимости от того, какие значения принимает другая.
Так как понятие статистической зависимости относится к осредненным условиям , прогнозы не могут быть безошибочными. Применяя некоторые вероятностные методы , можно вычислить вероятность того, что ошибка прогноза не выйдет за определенные границы.
В исследованиях между изучаемыми признаками чаще всего наблюдаются корреляционные взаимосвязи. (Связь роста с весом, прыжки в длину и бег на короткие дистанции).
Слайд 5функциональная взаимосвязь
Функциональной называется взаимосвязь, при которой каждому значению одного показателя соответствует

строго определенное значение другого.
Слайд 6Статистическая взаимосвязь
Статистической взаимосвязью называется взаимосвязь, при которой одному значению первого показателя может

соответствовать несколько значений второго показателя.
Слайд 7Корреляционный анализ
Корреляционный анализ состоит в определении степени связи между двумя случайными величинами

(Y и X).
Слайд 8Основные задачи корреляционного анализа
определение формы связи (линейная, нелинейная);
определение направления связи

(положительная связь или отрицательная);
определение степени или тесноты взаимосвязи (слабая, средняя, сильная).
Слайд 14Диапазон коэффициента корреляции
.
-1 ≤ r ≤ 1

Слайд 15Построение корелляционного поля
Пару случайных чисел x и y,представляющих собой результаты измерения спортивных

результатов, можно изобразить графически в прямоугольной системе координат в виде совокупности точек с координатами x, y. Множество этих точек образуют графическую зависимость, называемую корреляционным полем или диаграммой рассеивания.
Визуальный анализ графика позволяет выявить как форму, так и направленность и силу взаимосвязи.
Корреляционное поле необходимо обвести по краю и рассмотреть полученную фигуру, если обведенный ареал напоминает эллипс, то речь идет о линейной зависимости.
Далее производится анализ графика, если эллипс узкий, то зависимость сильная. По графику можно увидеть положительную или отрицательную направленность.
Слайд 17Критерии оценки силы взаимосвязи в корреляции
(функциональная зависимость)
(сильная зависимость)
(зависимости нет)
(очень слабая зависимость)
(слабая

зависимость)
(средняя зависимость)
Слайд 18Коэффициент детерминации
Коэффициент детерминации (R²) -величина квадрата коэффициента корреляции.
Величина R² показывает долю

(%) части варьирования одного из признаков, связанную с варьированием другого
Слайд 19Коэффициент корреляции Браве-Пирсона

Слайд 20Вычисление коэффициента корреляции Браве-Пирсона

Слайд 21Этапы проверки гипотезы
1. Задаются уровнем значимости α=0,05.
2. Формулируют гипотезы Н0: r=0

Н1: r≠0
3. Рассчитывают эмпирическое значение t критерия Стьюдента
4. Определяют критическое значение критерия tкр
5. Сравнивают эмпирическое значение критерия с критическим
Слайд 22Пример исследования корреляции
Результаты метания диска и толкания ядра

Слайд 23Корреляционное поле
Рис. 6. Корреляционное поле

Слайд 25Вычисление суммы значений xi и yi

Слайд 26Определение средних значений признаков xi и yi

Слайд 28Значение коэффициента корреляции Браве-Пирсона

Слайд 29Коэффициент корреляции лежит в интервале , поэтому можно сделать предположение о том,

что между результатами, показанными спортсменами в метании диска, и результатами, показанными ими в толкании ядра, существует линейная положительная сильная статистическая взаимосвязь.
Слайд 30Коэффициент детерминации
Таким образом, 70% взаимосвязи между двумя наборами данных объясняется их

взаимовлиянием. Остальная часть вариации обусловлена воздействием других неучтенных причин.
Слайд 31Вывод о статистической значимости коэффициента корреляции
Между результатами, показанными спортсменами в метании

диска, и результатами, показанными ими в толкании ядра, существует значимая положительная взаимосвязь.
Слайд 32Коэффициенты вариации
Поскольку коэффициент вариации у результатов в метании диска больше, чем

у результатов в толкании ядра, то этот признак варьирует сильнее
Слайд 33Находим x и y
Заполняем таблицу
Находим
Находим
Алгоритм №1 вычисления коэффициента корреляции

Слайд 345. Проверка значимости выборочного коэффициента корреляции
Вычислить наблюдаемое значение критерия
Сравнить числа

|Тнабл| и Tкрит :
если |Тнабл| < Tкрит , то принять гипотезу H0;
если |Тнабл| > Tкрит то гипотеза H0 отвергается
Слайд 36Вспомогательная таблица для расчета коэффициента корреляции

Слайд 37Алгоритм №2 вычисления коэффициента корреляции
Находим x и y
Заполняем таблицу
Находим ;
Находим

Слайд 38
Находим выборочный корреляционный момент:
Находим выборочный коэффициент корреляции:

Слайд 397. Найти оценки параметров линейной
регрессии по выборке.
8. Изобразить заданные точки

и
прямую регрессии.
Уравнение искомой прямой






































 Векторный анализ -теория поля. Типы векторных полей. Лекция 18
Векторный анализ -теория поля. Типы векторных полей. Лекция 18 Аналитическая геометрия в пространстве
Аналитическая геометрия в пространстве Дифференциальное исчисление для функции нескольких переменных. Метрические пространства
Дифференциальное исчисление для функции нескольких переменных. Метрические пространства Применение векторов к решению задач. 9 класс
Применение векторов к решению задач. 9 класс Уравнение
Уравнение Занимательная математика. 2 класс
Занимательная математика. 2 класс Математический диктант. Задачи. 1 класс
Математический диктант. Задачи. 1 класс Пространство IsR центрированных интервалов
Пространство IsR центрированных интервалов Симметрия. Виды симметрии
Симметрия. Виды симметрии Прибавить и вычесть 4
Прибавить и вычесть 4 Вывод формулы длины окружности и площади круга
Вывод формулы длины окружности и площади круга Усный счёт Заселяем домики
Усный счёт Заселяем домики Прямая, кривая, ломаная
Прямая, кривая, ломаная Решение задач. Продолжи ряд чисел
Решение задач. Продолжи ряд чисел Свойства арифметического корня
Свойства арифметического корня Основные принципы комбинаторики
Основные принципы комбинаторики Свойства сложения. 2 класс
Свойства сложения. 2 класс Презентация к уроку математики 6 класса учителя математики НОУ СОШ «Азъ Буки Веди» Ивахненко Натальи Геннадьевны
Презентация к уроку математики 6 класса учителя математики НОУ СОШ «Азъ Буки Веди» Ивахненко Натальи Геннадьевны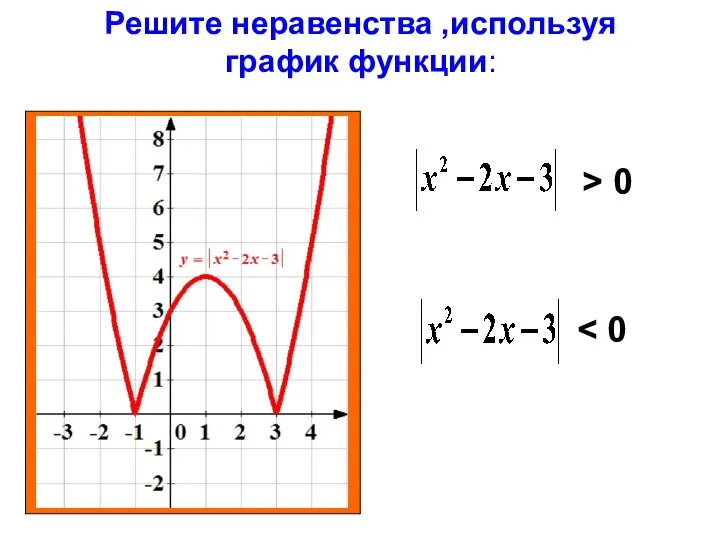 Решите неравенства ,используя график функции: x 2x 3 > 0
Решите неравенства ,используя график функции: x 2x 3 > 0 Нахождение числа по заданному значению его дроби
Нахождение числа по заданному значению его дроби Решение задач. Периметр и площадь
Решение задач. Периметр и площадь Уравнения высших степеней
Уравнения высших степеней арифметический корень (1)
арифметический корень (1) Правильные многогранники и ИДСЗ
Правильные многогранники и ИДСЗ Волшебная страна - Геометрия. Занятие 4
Волшебная страна - Геометрия. Занятие 4 Единицы времени. Час. минута
Единицы времени. Час. минута Основы теории MOM метода. Настройка параметров EM симулятора на основе метода MOM
Основы теории MOM метода. Настройка параметров EM симулятора на основе метода MOM Корни уравнения
Корни уравнения