Содержание
- 2. Все, что окружает нас, состоит из геометрических фигур
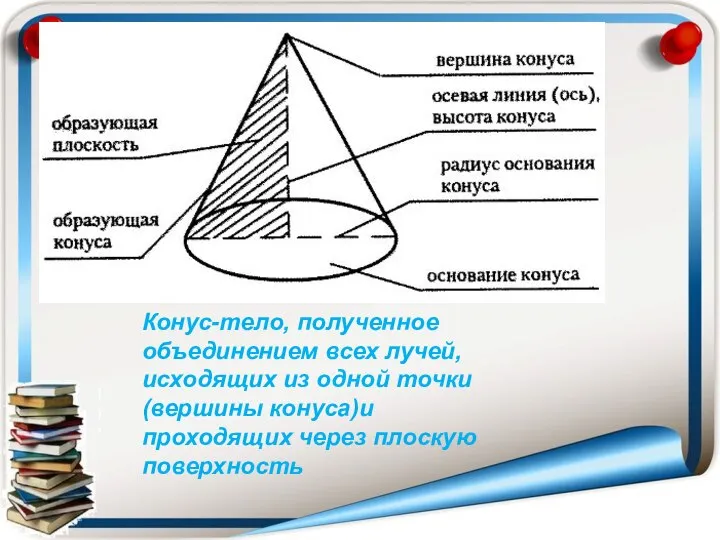
- 3. Конус-тело, полученное объединением всех лучей, исходящих из одной точки(вершины конуса)и проходящих через плоскую поверхность
- 5. Актуальность работы: данная работа представляет собой исследование, в котором в качестве объекта рассматривается применение конуса в
- 6. Цель работы: доказать универсальность этой фигуры и показать разнообразие применения свойств конуса в различных областях жизнедеятельности
- 7. Задачи: изучить различные печатные источники и СМИ по заявленной теме; изучить историю математического описания конуса; рассмотреть
- 8. Гипотеза: возможно, при одном и том же объеме вместимость упаковок конусной формы выше, чем упаковок в
- 9. Методы исследования: изучение и анализ справочных материалов, материалов математических журналов, научно-популярной литературы; наблюдение над использованием предметов
- 10. Геометрия в ранний период своего развития достигла особенно высокого уровня в Египте
- 11. Исследованиям конуса и других геометрических фигур положил начало Евклид в своей книге, которая так и называлась
- 12. Аполлоний Пергский – древнегреческий математик и астроном, ученик Евклида Конической поверхностью называется поверхность, образованная прямыми (образующими
- 13. В жизни мы нередко встречаемся с конусами. Например, используем горшки для цветов, имеющие форму усечённого конуса
- 14. Находясь на площади, на которой проходит митинг или демонстрация, мы можем увидеть человека с рупором в
- 15. Церковный колокол – металлическое изделие в виде полого усечённого конуса с подвешенным внутри него для звона
- 16. Используется конус и в архитектуре башен и куполов
- 17. Причудливые колпаки клоунов, колпак Санта - Клауса, новогодняя ёлка – конусы, придающие атмосферу праздника и веселья
- 18. Подарить эстетическое наслаждение поможет свернутая в форме конуса упаковка для букета цветов или духи в конусной
- 19. Рассмотрим преимущества использования предметов в форме конуса и докажем, что цветочная упаковка конической формы гораздо экономичнее
- 20. Возможно, при одном и том же объеме вместимость упаковок конусной формы выше, чем упаковок в форме
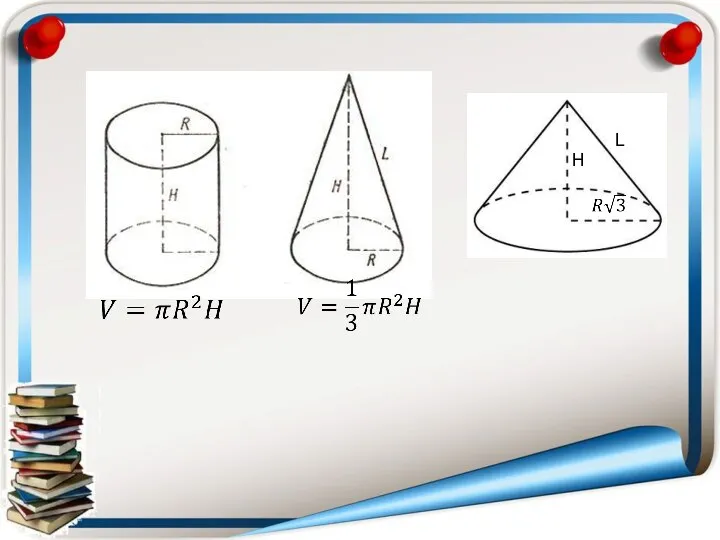
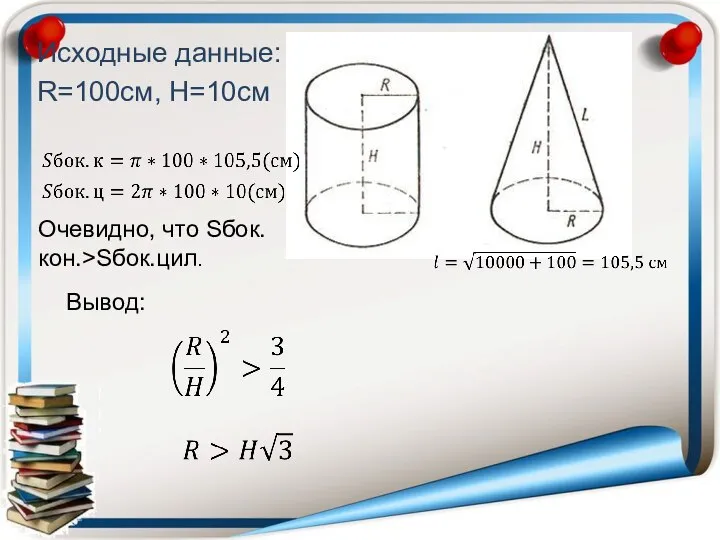
- 21. H L
- 22. Вывод: очевидно, что площадь основания конуса больше площади основания цилиндра. Следовательно, использовать конусную упаковку выгоднее, так
- 23. Предположим, при одном и том же объеме упаковок в форме конуса и цилиндра расход материала на
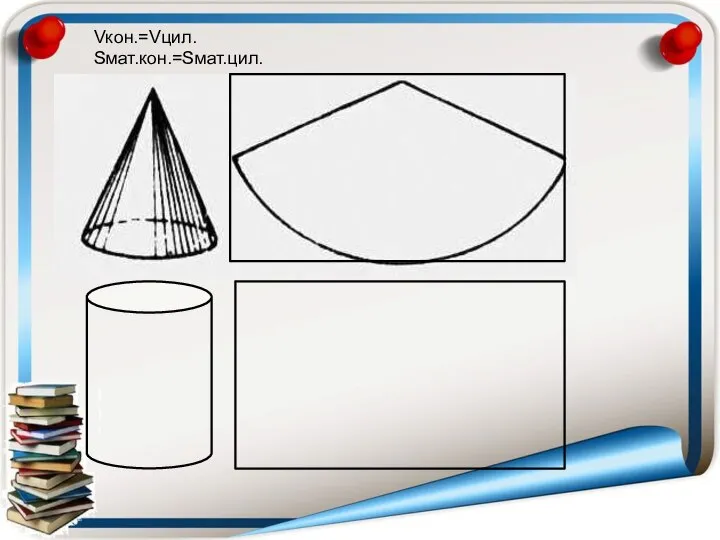
- 24. Vкон.=Vцил. Sмат.кон.=Sмат.цил.
- 25. Вывод: площадь материала для создания упаковки в форме конуса, (объемом равному площади цилиндра), меньше площади материала
- 26. Возможно, использовать упаковку в форме конуса выгоднее, чем упаковку в форме цилиндра для одного и того
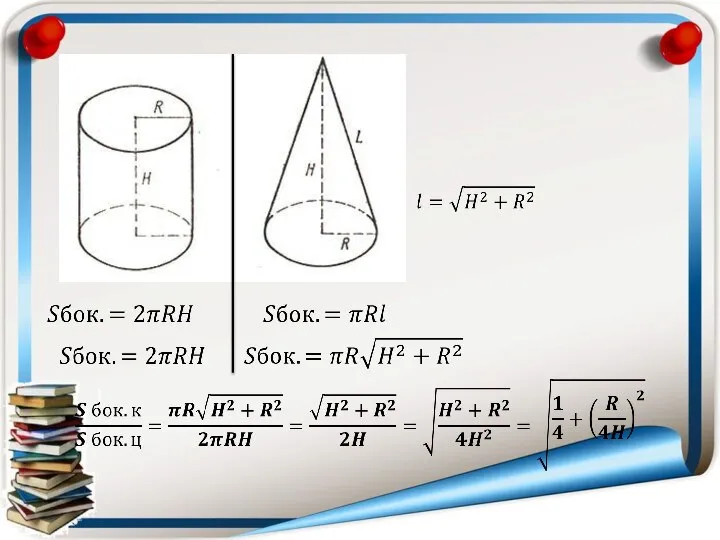
- 28. Исходные данные: R=100см, H=10см Очевидно, что Sбок.кон.>Sбок.цил. Вывод:
- 29. Из проведенного исследования стало очевидно, если R цветочной упаковки больше, чем стебель цветка, то выгоднее использовать
- 30. ВЫВОДЫ: 1. Конус - универсальная геометрическая форма, свойства которой часто используются в разных сферах жизни человека:
- 31. 4. Упаковка в форме конуса выгоднее при условии, когда цветы имеют длинный стебель и их количество
- 32. Присмотритесь повнимательнее к окружающим нас предметам - и вы увидите много интересных и полезных вещей!
- 34. Скачать презентацию


























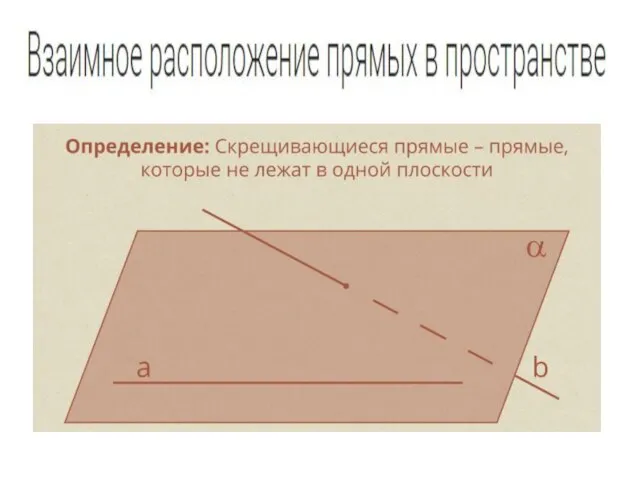 Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве Решение задач на временные отношения (подготовка к олимпиаде по математике обучающихся 4 класса)
Решение задач на временные отношения (подготовка к олимпиаде по математике обучающихся 4 класса) Симметрия. Виды симметрии
Симметрия. Виды симметрии Презентация на тему Арифметические действия с числами
Презентация на тему Арифметические действия с числами  Построение графиков элементарных функций
Построение графиков элементарных функций Шарады, метаграммы, логогрифы
Шарады, метаграммы, логогрифы Решение задач на увеличение числа в несколько раз
Решение задач на увеличение числа в несколько раз Формула перехода к новому основанию логарифма
Формула перехода к новому основанию логарифма Модуль числа (часть 2)
Модуль числа (часть 2) Обыкновенная дробь
Обыкновенная дробь Формулы сокращенного умножения a b
Формулы сокращенного умножения a b Сложение и вычитание вида +- 1
Сложение и вычитание вида +- 1 Ломаные на узорах
Ломаные на узорах Прибавление и вычитание числа 2
Прибавление и вычитание числа 2 Урок 9 (29.09.22) Решение задач
Урок 9 (29.09.22) Решение задач Угол и биссектриса
Угол и биссектриса Своя игра. Вычисление корней
Своя игра. Вычисление корней Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Четыре замечательные точки треугольника. 8 класс
Четыре замечательные точки треугольника. 8 класс Десятичная дробь. Графический диктант
Десятичная дробь. Графический диктант Матрицы и определители
Матрицы и определители Презентация на тему Прибавление числа к сумме (1 класс)
Презентация на тему Прибавление числа к сумме (1 класс)  Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Составление и решение текстовых задач на увеличение и уменьшение числа на несколько единиц
Составление и решение текстовых задач на увеличение и уменьшение числа на несколько единиц ИПАР по математике. Задача на проценты. Тема: математика в профессии моих родителей
ИПАР по математике. Задача на проценты. Тема: математика в профессии моих родителей Уравнения и неравенства с одной переменной. Урок разноуровнего обобщающего повторения
Уравнения и неравенства с одной переменной. Урок разноуровнего обобщающего повторения Деление суммы на число
Деление суммы на число Цепочка бусин
Цепочка бусин