Слайд 21.1. Понятие первообразной функции
и неопределенного интеграла.
Основные свойства неопределенного интеграла
Интегральное исчисление фактически

гораздо старше дифференциального, поскольку вычисление площадей, поверхностей и объемов занимало величайших математиков, начиная с античных времен. Среди них были Архимед, Кеплер, Кавальери, Вивиани, Ферма, Грегори СентВинсент, Гулдин, Грегори, Барроу. Решающий прорыв наступил, когда Ньютон, Лейбниц и И. Бернулли независимо открыли, что интегрирование является операцией, обратной дифференцированию, и, следовательно, все достижения вышеупомянутых исследователей можно свести к нескольким правилам дифференцирования.
Слайд 3Определение 1.1. Функция F(x) называется первообразной для f(x) на интервал (a, b),

если F′(x) = f(x) в любой точке интервала (a, b).
Примеры:
1) f(x)=0, F(x)=C (Const), (-∞,∞)
2) f(x)=a (Const), F(x)=ax, (-∞,∞)
3) f(x)=cos x, F(x)=sin x, (-∞,∞)
4) f(x)=1/x, F(x)=ln x, (0,∞)
5) f(x)=-2sin 2x, F1(x)= cos 2x, F2(x)= -2sin2x
Слайд 4Теорема 1.1. Если функции F1(x) и F2(x) являются первообразными для f(x) на

интервал (a, b), то в любой точке интервала (a, b) выполняется равенство F1(x) - F2(x) = С, где С – произвольная константа.
Следствие. Если функция F1(x) – первообразная для f(x) на интервал (a, b), и F2(x) - другая первообразная, то в любой точке интервала (a, b) выполняется равенство F1(x) = F2(x) + С, где С – произвольная константа.
Пример. Функции ln |x| и ln|x| + sign x являются первообразными для 1/x на множестве X = (-∞,0)∪(0,∞), но их разность не является константой.
Слайд 7Таблица неопределенных интегралов

Слайд 8Основные свойства неопределенного интеграла.

Слайд 9Непосредственное интегрирование

Слайд 101.2. Интегрирование заменой переменной (подстановкой). Интегрирование по частям.










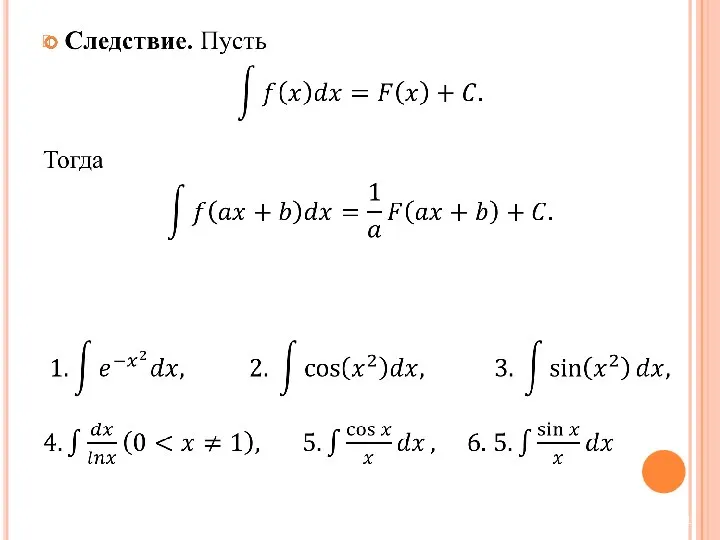
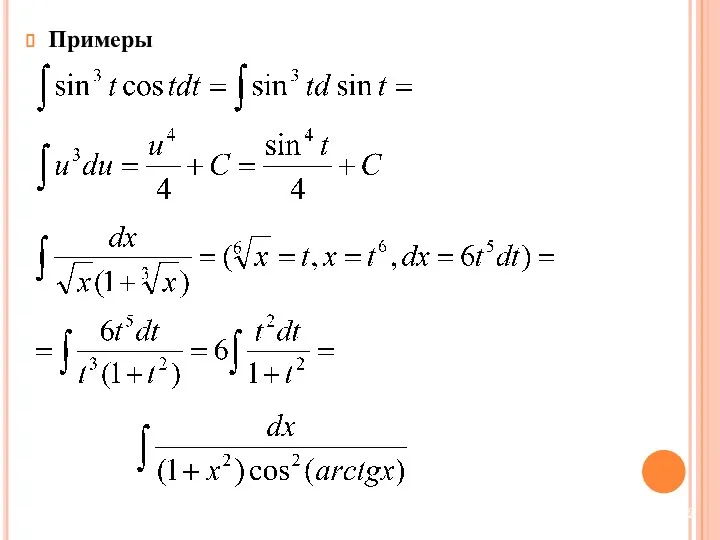

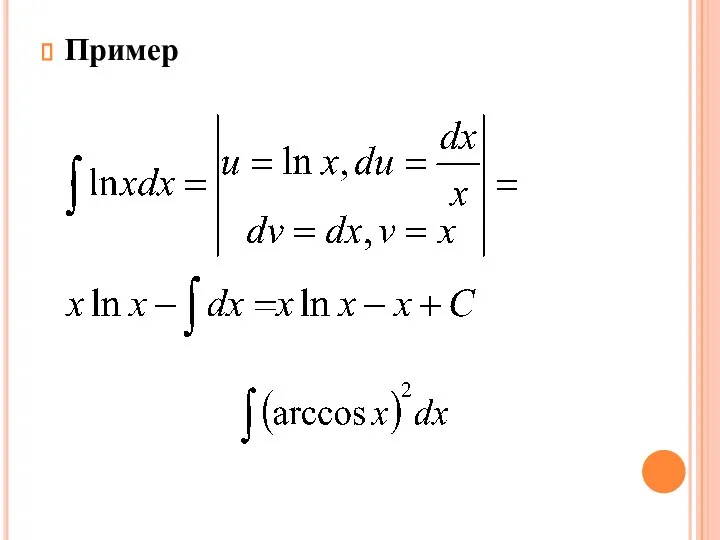
 Понятие функции
Понятие функции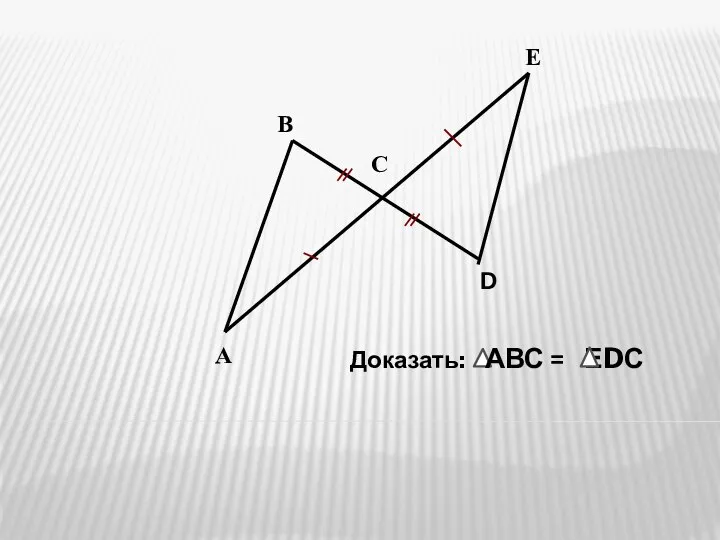 Признаки равенства треугольников. Решение задач
Признаки равенства треугольников. Решение задач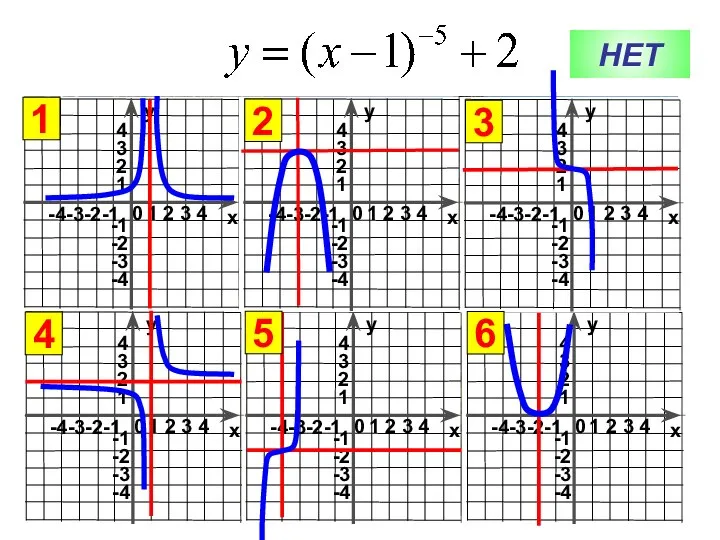 графики функций. Ошибка
графики функций. Ошибка Методы решения Слау. Метод Гаусса
Методы решения Слау. Метод Гаусса Variācijas, permutācijas, kombinācijas
Variācijas, permutācijas, kombinācijas Задачи на разрезание и перекраивание фигур
Задачи на разрезание и перекраивание фигур Презентация на тему Действия с векторами
Презентация на тему Действия с векторами  Приложение производной
Приложение производной Вычитание числа 2 (1 класс)
Вычитание числа 2 (1 класс) Допуски линейных размеров. Квалитет
Допуски линейных размеров. Квалитет Симметрия в природе
Симметрия в природе Решение задач на применение свойств прямоугольного треугольника. 7 класс
Решение задач на применение свойств прямоугольного треугольника. 7 класс Числовой коэффициент
Числовой коэффициент Квадратные уравнения. Устная разминка
Квадратные уравнения. Устная разминка Формула Стирлинга
Формула Стирлинга Старинные единицы измерения. Меры и массы и объемы
Старинные единицы измерения. Меры и массы и объемы Тригонометрические уравнения
Тригонометрические уравнения Сравнение двух прогрессий
Сравнение двух прогрессий Математика. Составные высказывания
Математика. Составные высказывания Множества точек на координатной плоскости, расстояние между точками координатной прямой
Множества точек на координатной плоскости, расстояние между точками координатной прямой Некоторые понятия о статистике, статистическом методе и термодинамике
Некоторые понятия о статистике, статистическом методе и термодинамике Математическая викторина (начальная школа)
Математическая викторина (начальная школа) Координатный луч
Координатный луч Векторы плоскости
Векторы плоскости Обыкновенные дроби. 5 класс
Обыкновенные дроби. 5 класс Площади четырёхугольников. Решение задач
Площади четырёхугольников. Решение задач Математика и физика здоровья
Математика и физика здоровья Решение задач на нахождение неизвестного вычитаемого
Решение задач на нахождение неизвестного вычитаемого