Слайд 3Расположение параболы в зависимости от величины дискриминанта

Слайд 4Расположение параболы в зависимости от величины дискриминанта
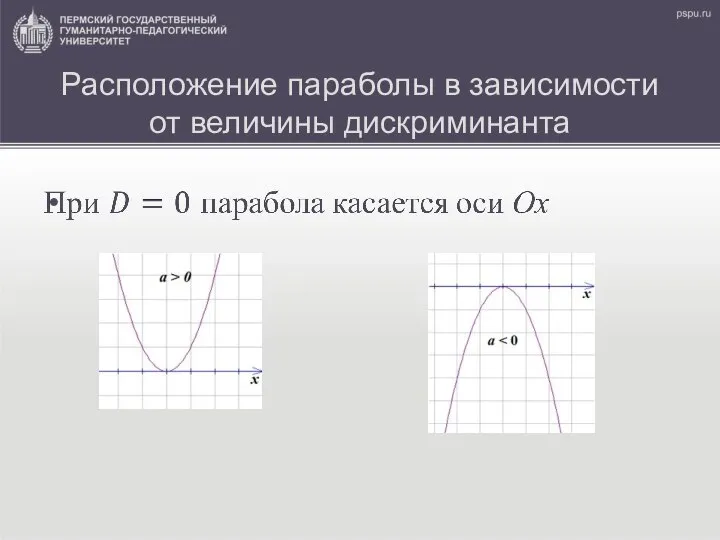
Слайд 5Расположение параболы в зависимости от величины дискриминанта
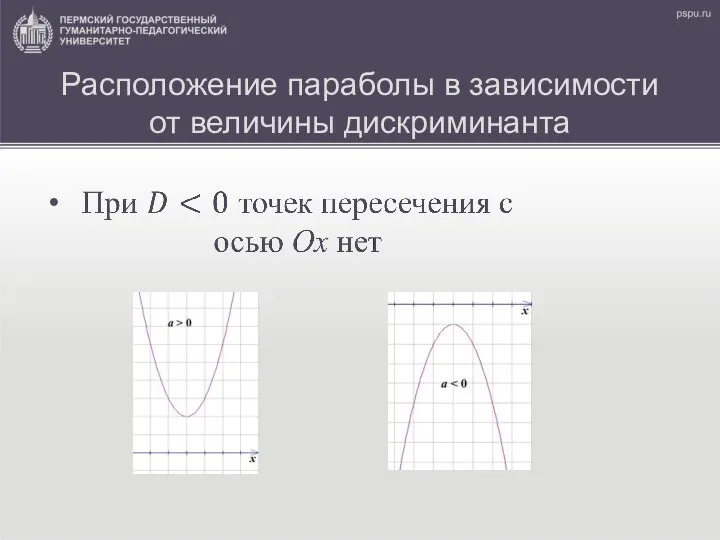
Слайд 9Разложение квадратного трёхчлена на множители

Слайд 15Определение. Если каждый корень уравнения (решение неравенства) А является корнем уравнения (решением

неравенства) В, то говорят, что уравнение (неравенство) В является следствием А.
Если уравнение (неравенство) не имеет решений, то из него следует любое другое уравнение или неравенство.





















 Угол между прямыми в пространстве
Угол между прямыми в пространстве mik_tangram
mik_tangram B7
B7 Вероятность события. Разбор задач
Вероятность события. Разбор задач Угол между векторами
Угол между векторами Секреты квадратных уравнений
Секреты квадратных уравнений Метод интервалов. Задания для устного счета. Упражнение 3
Метод интервалов. Задания для устного счета. Упражнение 3 Показательная функция. Уравнения
Показательная функция. Уравнения Деление квадрата на 4 равные части
Деление квадрата на 4 равные части Тренажёр по таблице умножения. Уровень PRO
Тренажёр по таблице умножения. Уровень PRO Составление систем уравнений Колмогорова. Математическое моделирование
Составление систем уравнений Колмогорова. Математическое моделирование Таблицы сложения и вычитания с числом 2
Таблицы сложения и вычитания с числом 2 Задачи на нахождение неизвестного по двум разностям
Задачи на нахождение неизвестного по двум разностям Задачи на движение. 11 класс
Задачи на движение. 11 класс Золотое сечение
Золотое сечение Меньше или больше ГБОУ ЦО № 354 учитель математики Иванова И.В.
Меньше или больше ГБОУ ЦО № 354 учитель математики Иванова И.В. Презентация на тему Порядок выполнения действий (5 класс)
Презентация на тему Порядок выполнения действий (5 класс)  Подобные слагаемые
Подобные слагаемые Решение неравенств второй степени с помощью эскиза параболы
Решение неравенств второй степени с помощью эскиза параболы Применение производных к исследованию функций и построение графиков
Применение производных к исследованию функций и построение графиков Выборочное наблюдение. Практическое занятие
Выборочное наблюдение. Практическое занятие Первый признак равенства треугольников
Первый признак равенства треугольников Системы линейных уравнений СЛУ
Системы линейных уравнений СЛУ Эконометрика
Эконометрика Случайные величины (лекция 3)
Случайные величины (лекция 3) Четные и нечетные функции. 10 класс
Четные и нечетные функции. 10 класс Разложение функций
Разложение функций Презентация на тему Теорема Пифагора и её применение
Презентация на тему Теорема Пифагора и её применение