Содержание
- 2. Оценки экстремума
- 3. Оценки экстремума т.е. погрешность решения задачи, невозможно. Возможность получения оценок экстремума по конечному числу испытаний зависит
- 4. Оценки экстремума для унимодальных функций Пример. Унимодальная функция на отрезке [0,8].
- 5. Оценки экстремума для унимодальных функций Пусть теперь в общем случае проведено k испытаний в точках и
- 6. Оценки экстремума для липшицевых функций Другим важным классом функций, допускающим построение оценок экстремума по конечному числу
- 7. Рассмотрим одномерную задачу Является ли непрерывная функция липшицевой? Является ли липшицева функция дифференцируемой? Является ли дифференцируемая
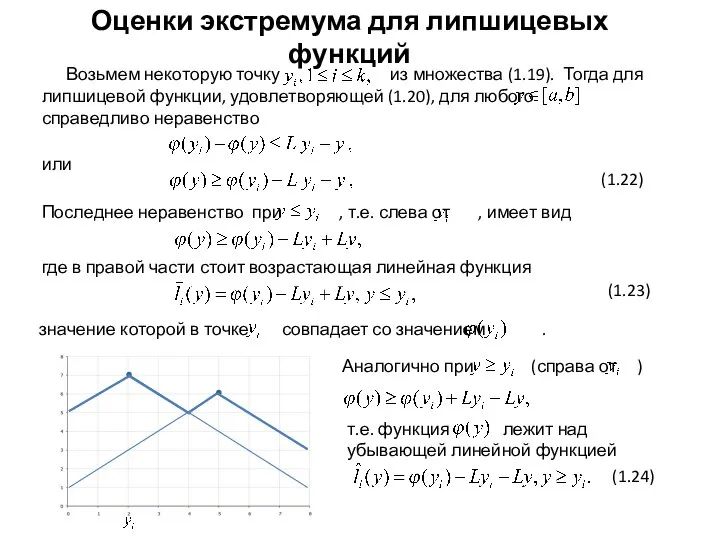
- 8. Возьмем некоторую точку из множества (1.19). Тогда для липшицевой функции, удовлетворяющей (1.20), для любого справедливо неравенство
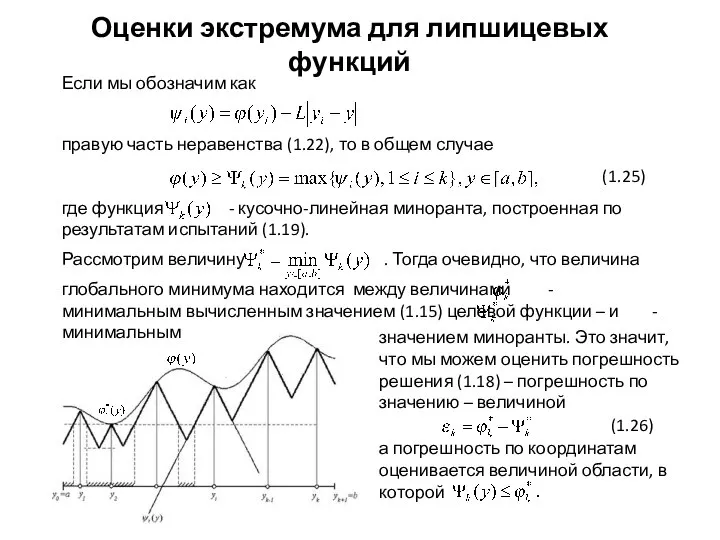
- 9. Если мы обозначим как правую часть неравенства (1.22), то в общем случае значением миноранты. Это значит,
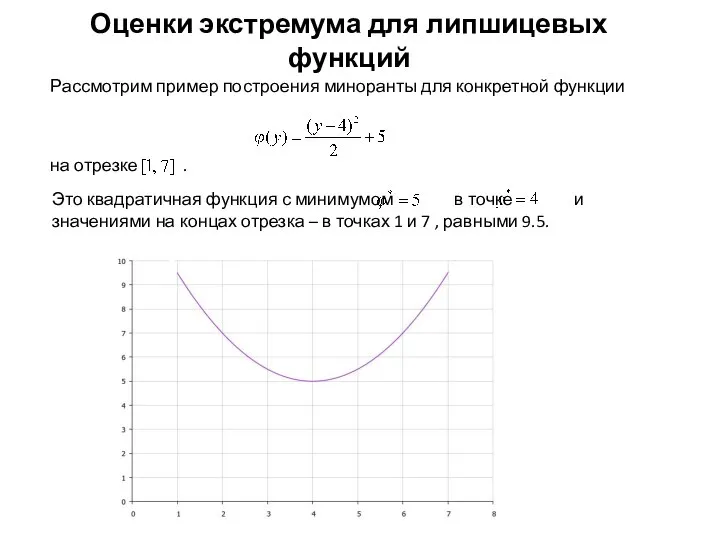
- 10. Оценки экстремума для липшицевых функций Рассмотрим пример построения миноранты для конкретной функции Это квадратичная функция с
- 11. Оценки экстремума для липшицевых функций Построим последовательно миноранту по 4 точкам:
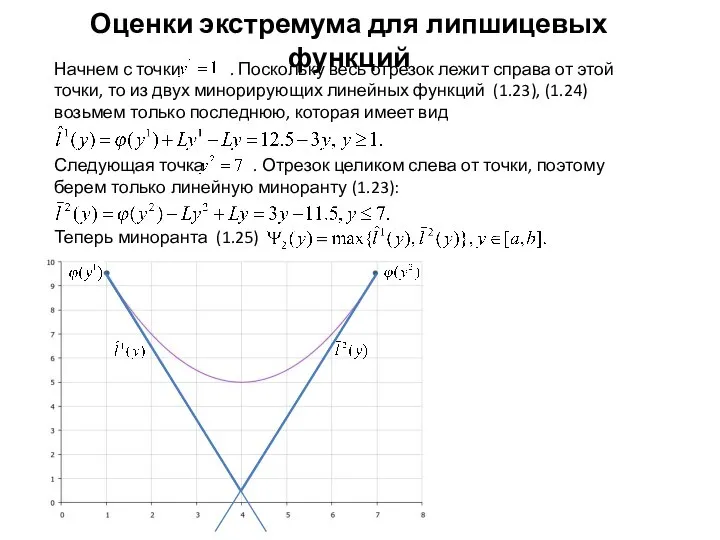
- 12. Оценки экстремума для липшицевых функций
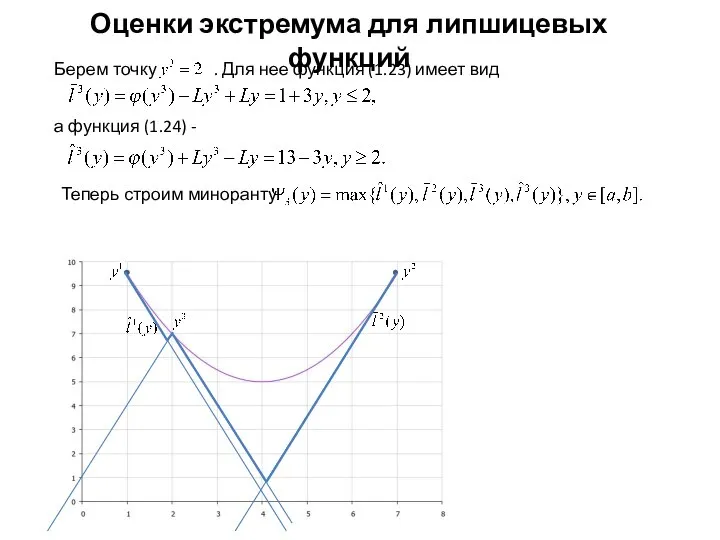
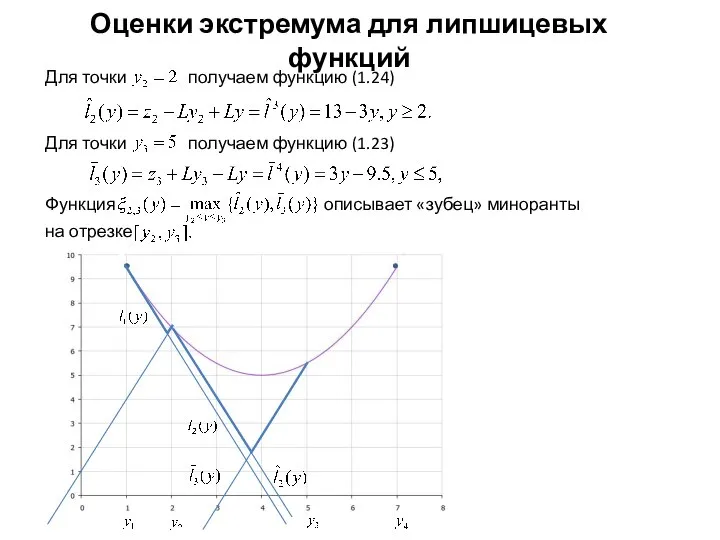
- 13. Оценки экстремума для липшицевых функций Берем точку . Для нее функция (1.23) имеет вид а функция
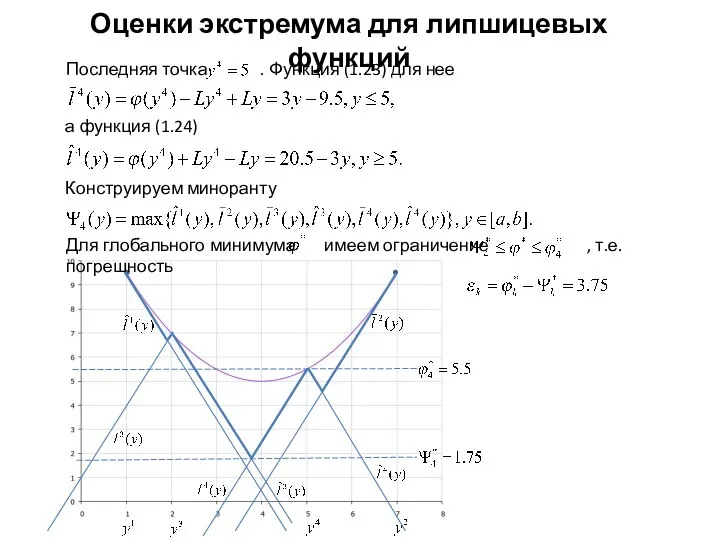
- 14. Оценки экстремума для липшицевых функций а функция (1.24) Конструируем миноранту
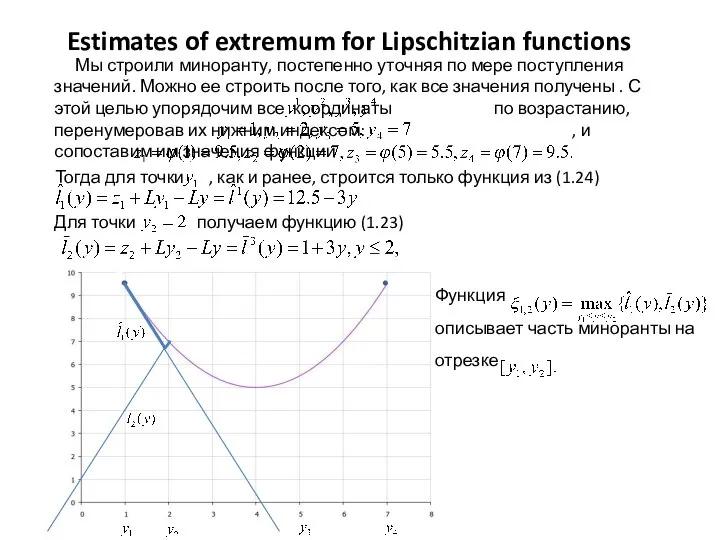
- 15. Estimates of extremum for Lipschitzian functions
- 16. Оценки экстремума для липшицевых функций
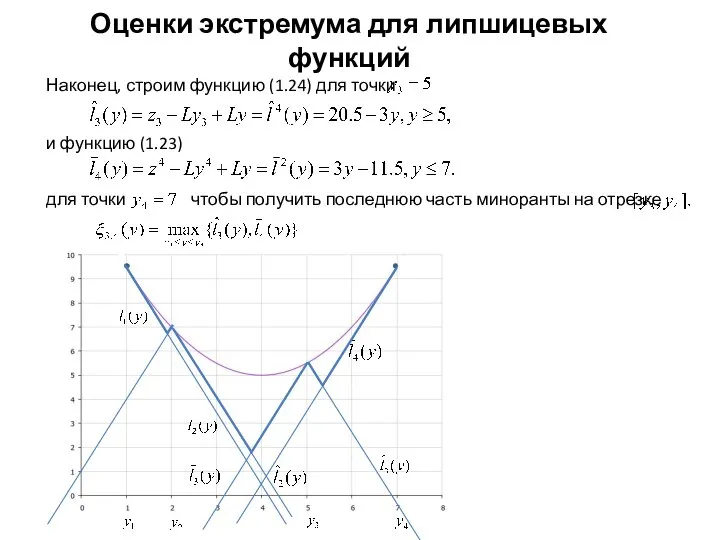
- 17. Оценки экстремума для липшицевых функций и функцию (1.23)
- 18. Оценки экстремума для липшицевых функций где Ее легко найти из равенства откуда
- 20. Скачать презентацию


![Оценки экстремума для унимодальных функций Пример. Унимодальная функция на отрезке [0,8].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1032612/slide-3.jpg)



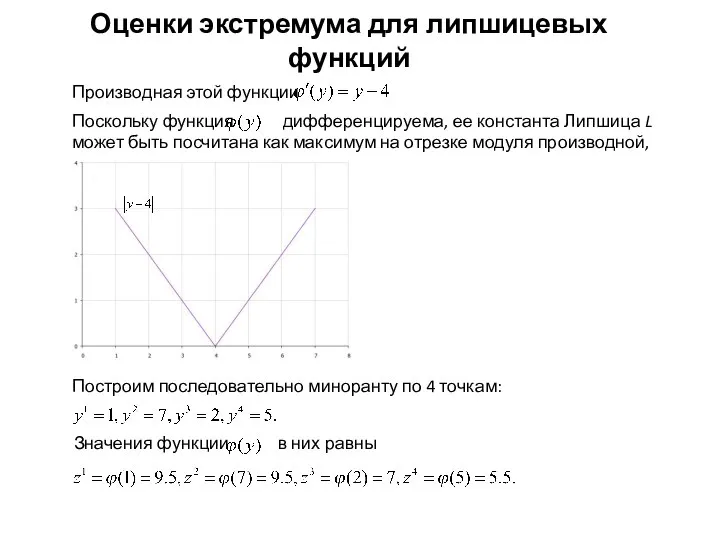

 Производная функции
Производная функции Презентация_к_уроку_Сложение_и_вычитание_алгебраических_дробей_с
Презентация_к_уроку_Сложение_и_вычитание_алгебраических_дробей_с Lektsia_4
Lektsia_4 Метод Крамера
Метод Крамера Проверочная работа по теме Кровь
Проверочная работа по теме Кровь Распределительный закон
Распределительный закон Применение интегральной технологии при изучении алгебраических уравнений
Применение интегральной технологии при изучении алгебраических уравнений Презентация на тему ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА
Презентация на тему ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА  Правильная пирамида
Правильная пирамида Цилиндр. Конус
Цилиндр. Конус Цифра 7
Цифра 7 Использование занимательных игровых упражнений при обучении элементарной математики для развития логического мышления дошкольн
Использование занимательных игровых упражнений при обучении элементарной математики для развития логического мышления дошкольн Элементы математической статистики
Элементы математической статистики Решение уравнений. 7 класс
Решение уравнений. 7 класс Линейные неравенства. 8 класс
Линейные неравенства. 8 класс Введение в стереометрию. Аксиомы стереометрии и некоторые следствия из аксиом. 10 класс
Введение в стереометрию. Аксиомы стереометрии и некоторые следствия из аксиом. 10 класс Линейная функция. Работа по графику
Линейная функция. Работа по графику Круг. Окружность. Длина окружности. Площадь круга. 6 класс
Круг. Окружность. Длина окружности. Площадь круга. 6 класс Математика. Лекция
Математика. Лекция Пирамида. Высрта пирамиды
Пирамида. Высрта пирамиды Модели пирамид
Модели пирамид Угол между прямой и плоскостью
Угол между прямой и плоскостью Устные приёмы сложения и вычитания в пределах 100. Урок математики во 2 классе
Устные приёмы сложения и вычитания в пределах 100. Урок математики во 2 классе Вариационная форма
Вариационная форма Комплексные числа
Комплексные числа Параллельность плоскостей
Параллельность плоскостей Конус. Поверхность конуса
Конус. Поверхность конуса Таблица умножения. Тренажер
Таблица умножения. Тренажер