Содержание
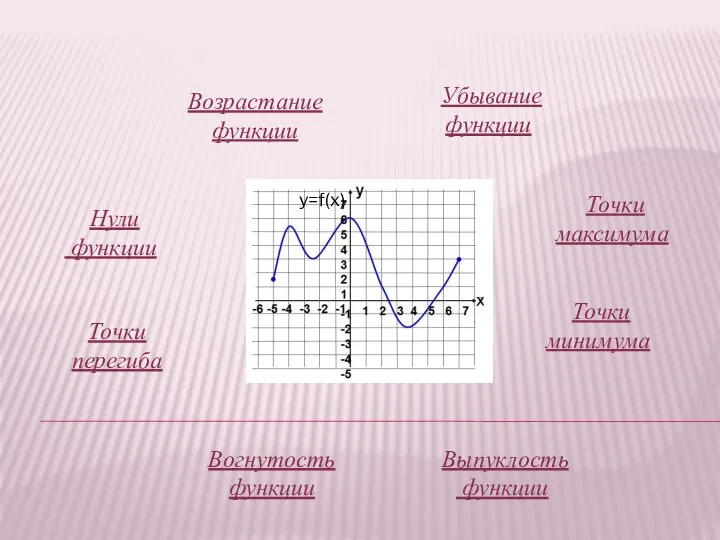
- 2. Вогнутость функции Точки максимума Точки минимума Точки перегиба Убывание функции Выпуклость функции Нули функции y=f(x) Возрастание
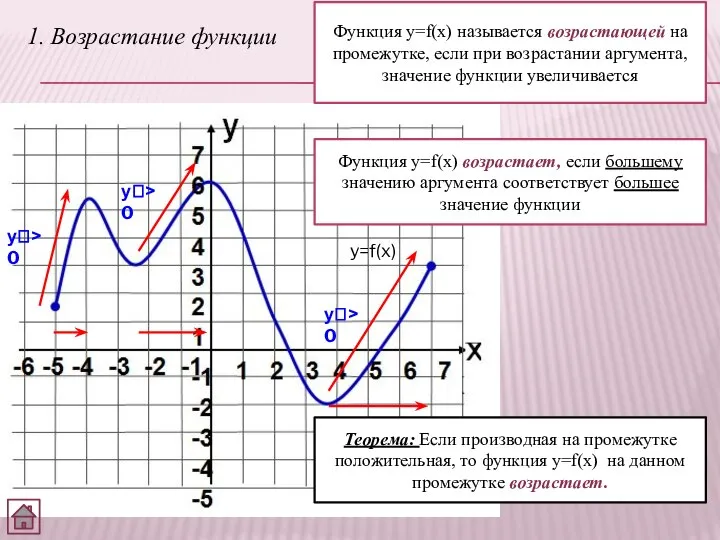
- 3. 1. Возрастание функции Функция y=f(x) называется возрастающей на промежутке, если при возрастании аргумента, значение функции увеличивается
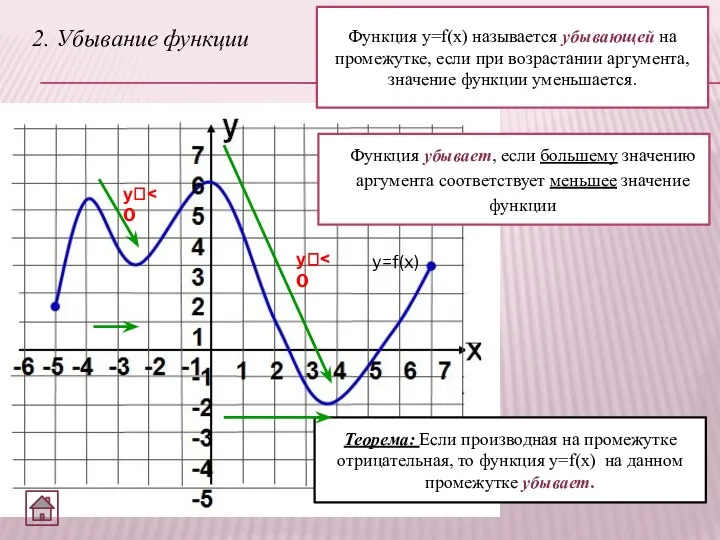
- 4. 2. Убывание функции Функция y=f(x) называется убывающей на промежутке, если при возрастании аргумента, значение функции уменьшается.
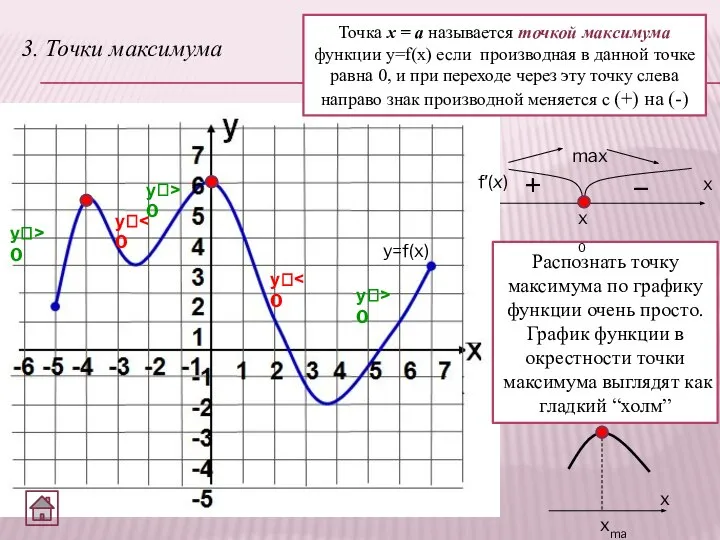
- 5. 3. Точки максимума Точка х = а называется точкой максимума функции y=f(x) если производная в данной
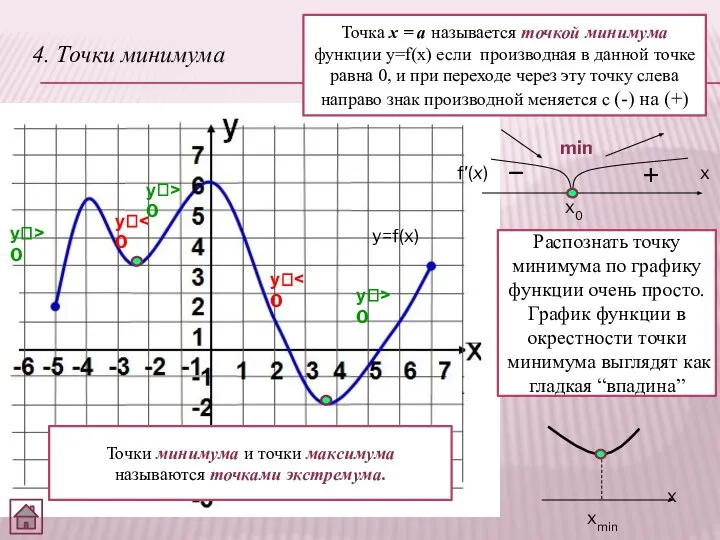
- 6. 4. Точки минимума Точка х = а называется точкой минимума функции y=f(x) если производная в данной
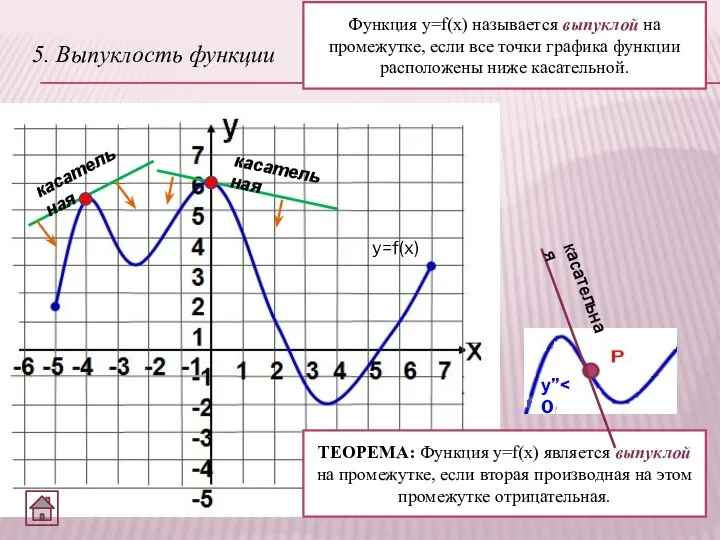
- 7. 5. Выпуклость функции Функция y=f(x) называется выпуклой на промежутке, если все точки графика функции расположены ниже
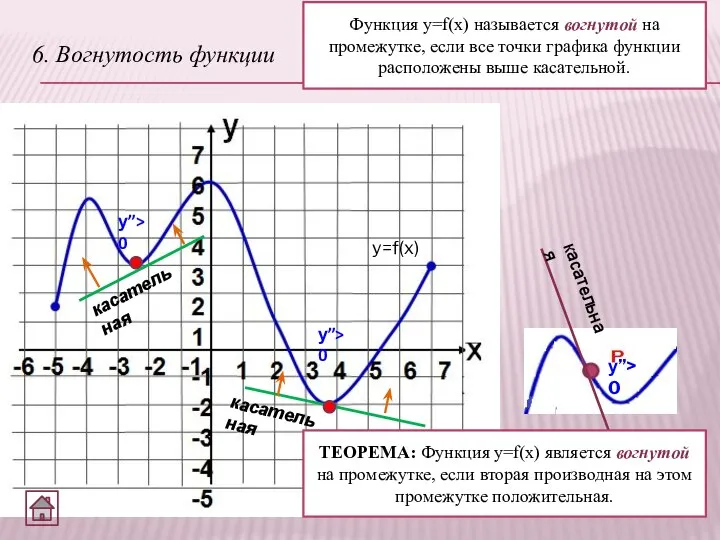
- 8. 6. Вогнутость функции Функция y=f(x) называется вогнутой на промежутке, если все точки графика функции расположены выше
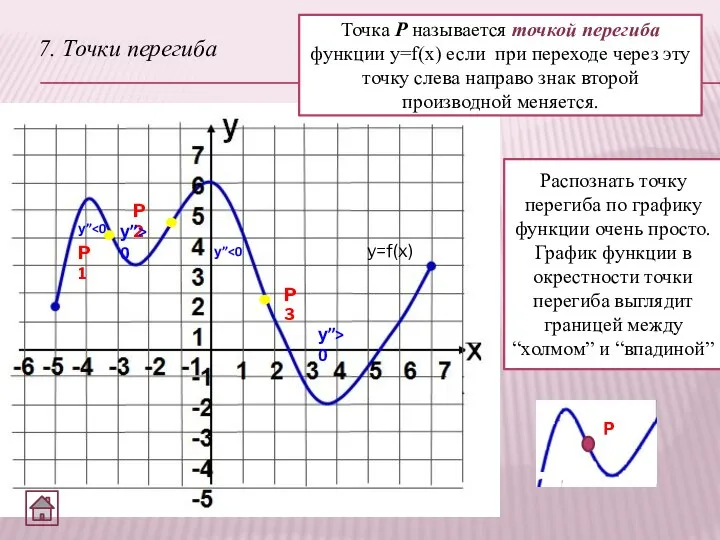
- 9. 7. Точки перегиба P1 Точка Р называется точкой перегиба функции y=f(x) если при переходе через эту
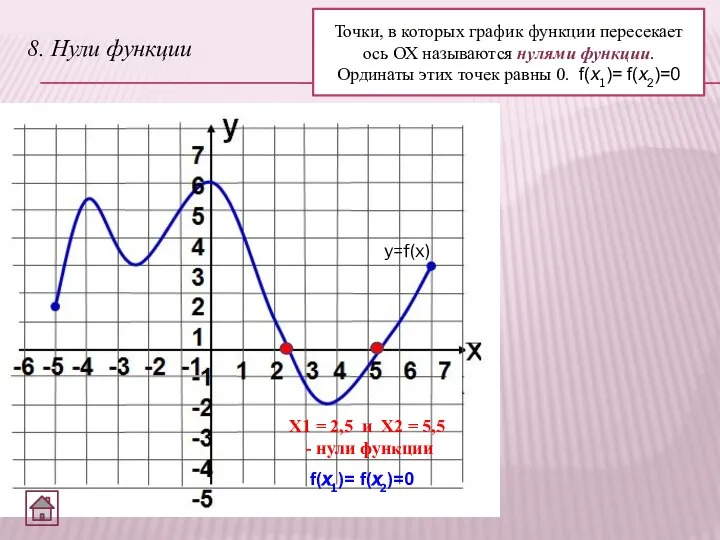
- 10. 8. Нули функции Точки, в которых график функции пересекает ось ОХ называются нулями функции. Ординаты этих
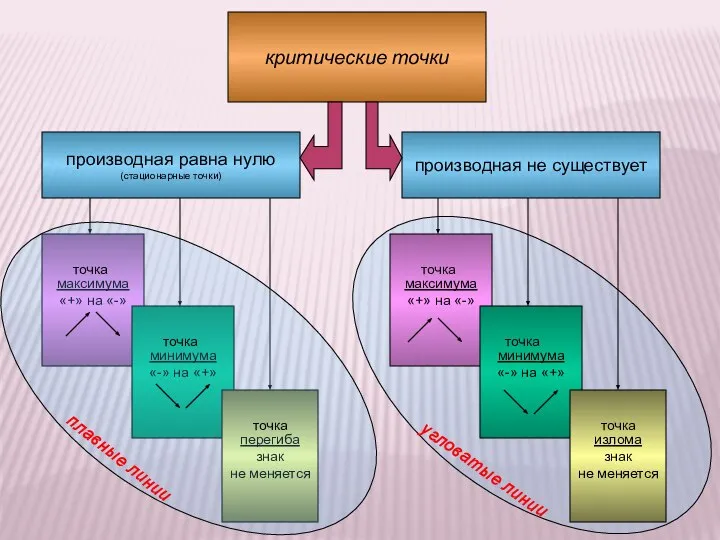
- 11. производная равна нулю (стационарные точки) критические точки производная не существует максимума «+» на «-» минимума «-»
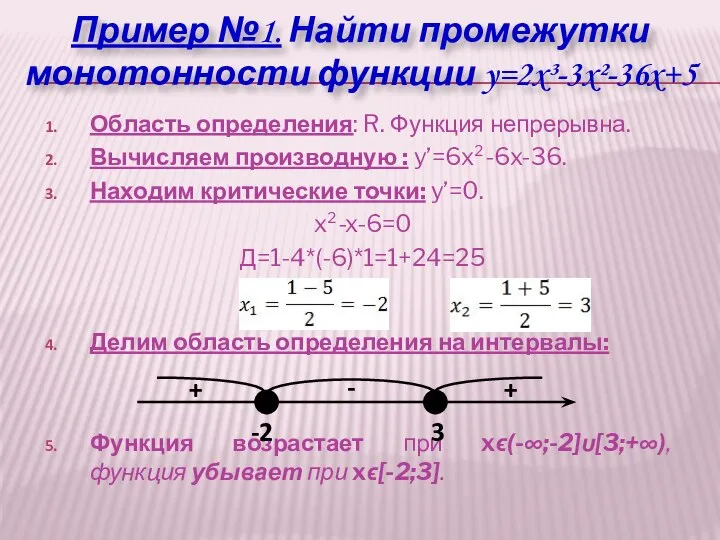
- 12. Область определения: R. Функция непрерывна. Вычисляем производную : y’=6x²-6x-36. Находим критические точки: y’=0. x²-x-6=0 Д=1-4*(-6)*1=1+24=25 Делим
- 13. Область определения: R (х-любое) Функция непрерывна. Вычисляем производную : y’=-6x²-6x+12. Находим критические точки: y’=0. -x²-x+2=0 Д=1-4*(-1)*2=1+8=9
- 14. ПРИМЕР №4. НАЙТИ ЭКСТРЕМУМЫ ФУНКЦИИ F(X)=X4-4X3 ООФ x-любое f '(x)=(x4-4x3)’ =4x3-4∙3x2= 4x3-12x2 f '(x)=0 4x3-12x2=0 4x2(x-3)=0
- 15. Пример №7. Найти экстремумы функции y=x3+3x2+9x-6. Решение: Находим область определения функции: D(y)=R. Находим производную: y’=(x3+3x2+9x-6)’=3x2+6x+9. Приравниваем
- 16. АЛГОРИТМ НАХОЖДЕНИЯ ЭКСТРЕМУМОВ ФУНКЦИИ Пусть дана функция f(x) 1. Найти ООФ 2. Найти производную f '(x)
- 17. СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ Алгоритм исследования функции с помощью производной: Пусть дана функция f(x) Область определения функции.
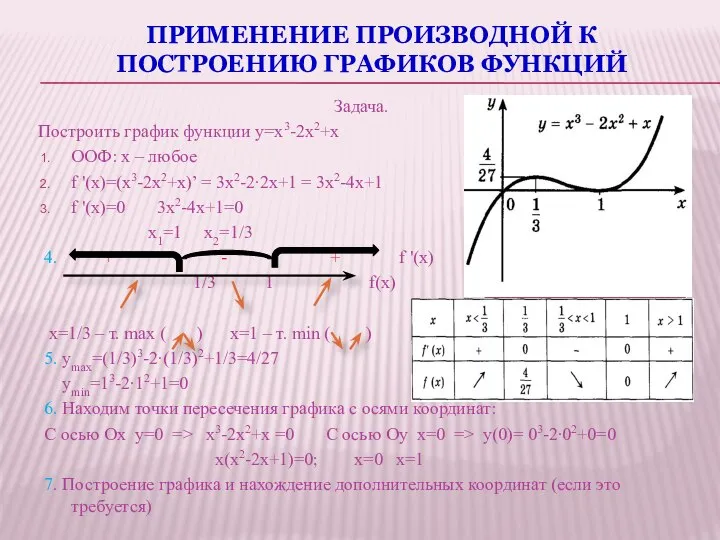
- 18. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ПОСТРОЕНИЮ ГРАФИКОВ ФУНКЦИЙ Задача. Построить график функции y=x3-2x2+x ООФ: x – любое f
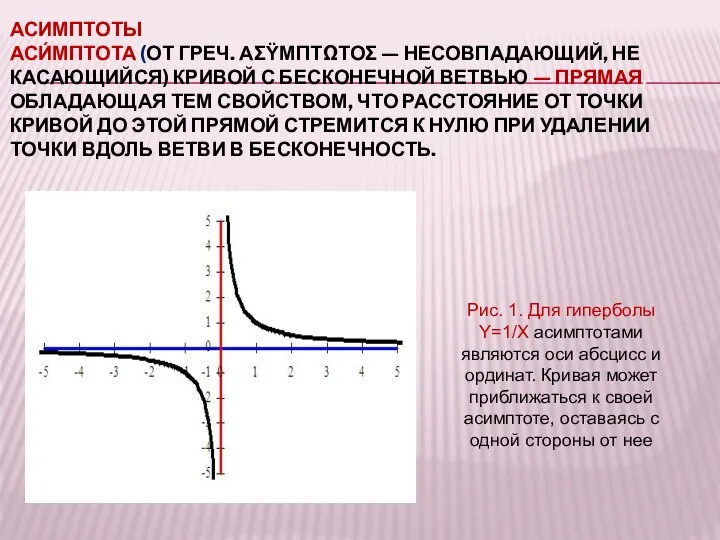
- 19. АСИМПТОТЫ АСИ́МПТОТА (ОТ ГРЕЧ. ΑΣΫΜΠΤΩΤΟΣ — НЕСОВПАДАЮЩИЙ, НЕ КАСАЮЩИЙСЯ) КРИВОЙ С БЕСКОНЕЧНОЙ ВЕТВЬЮ — ПРЯМАЯ, ОБЛАДАЮЩАЯ
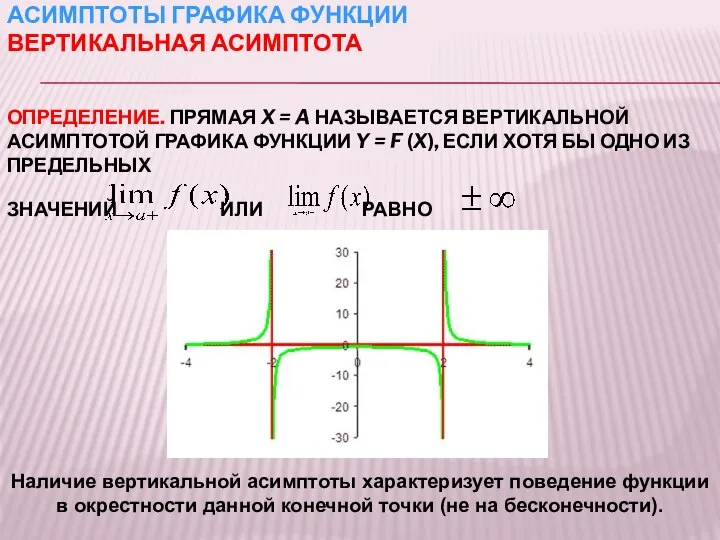
- 20. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ ВЕРТИКАЛЬНАЯ АСИМПТОТА ОПРЕДЕЛЕНИЕ. ПРЯМАЯ X = A НАЗЫВАЕТСЯ ВЕРТИКАЛЬНОЙ АСИМПТОТОЙ ГРАФИКА ФУНКЦИИ Y
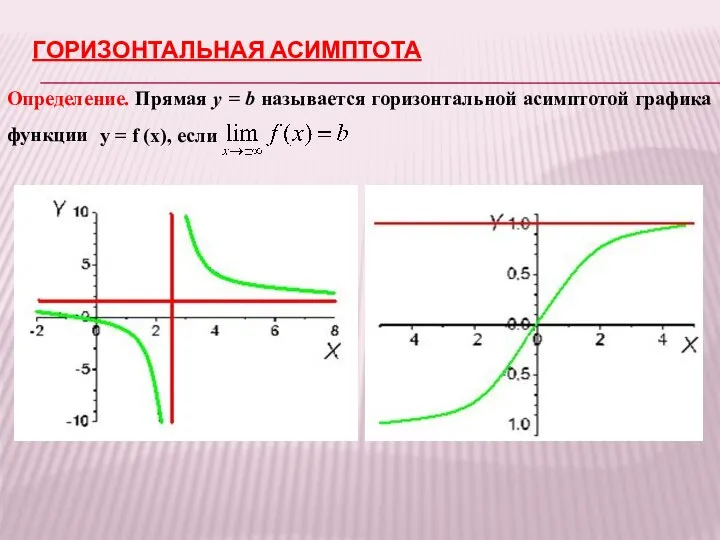
- 21. ГОРИЗОНТАЛЬНАЯ АСИМПТОТА Определение. Прямая y = b называется горизонтальной асимптотой графика функции y = f (х),
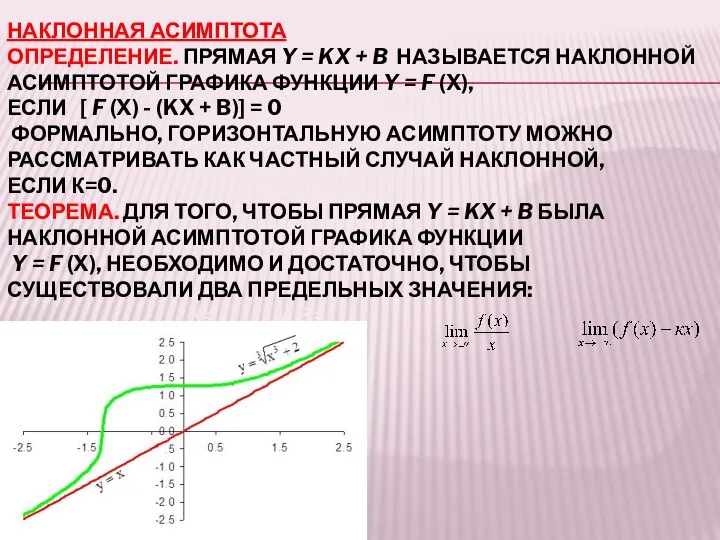
- 22. НАКЛОННАЯ АСИМПТОТА ОПРЕДЕЛЕНИЕ. ПРЯМАЯ Y = KX + B НАЗЫВАЕТСЯ НАКЛОННОЙ АСИМПТОТОЙ ГРАФИКА ФУНКЦИИ Y =
- 23. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ. РАССМОТРИМ ПОЛНУЮ СХЕМУ ИССЛЕДОВАНИЯ ФУНКЦИИ И ПОСТРОЕНИЯ ЕЕ ГРАФИКА ПО ПОЛУЧЕННЫМ РЕЗУЛЬТАТАМ ИССЛЕДОВАНИЯ.
- 24. Решение :
- 26. x
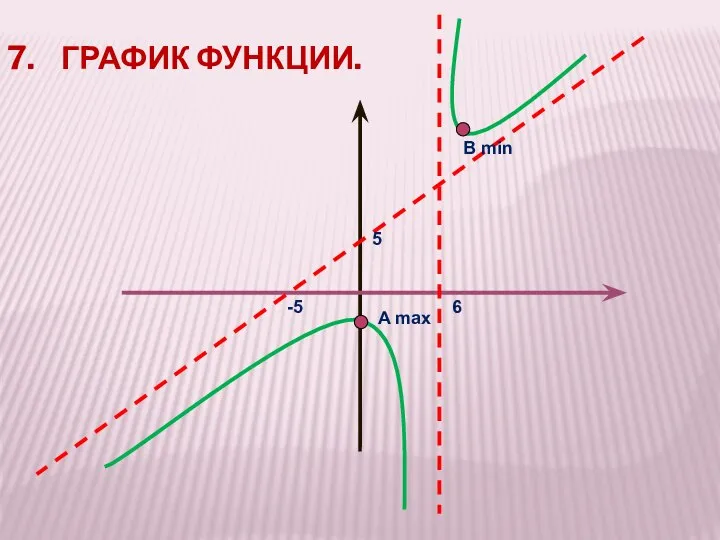
- 27. A max 7. ГРАФИК ФУНКЦИИ. -5 6 5 В min
- 28. РЕШЕНИЕ :
- 30. X
- 31. Точек перегиба нет. X
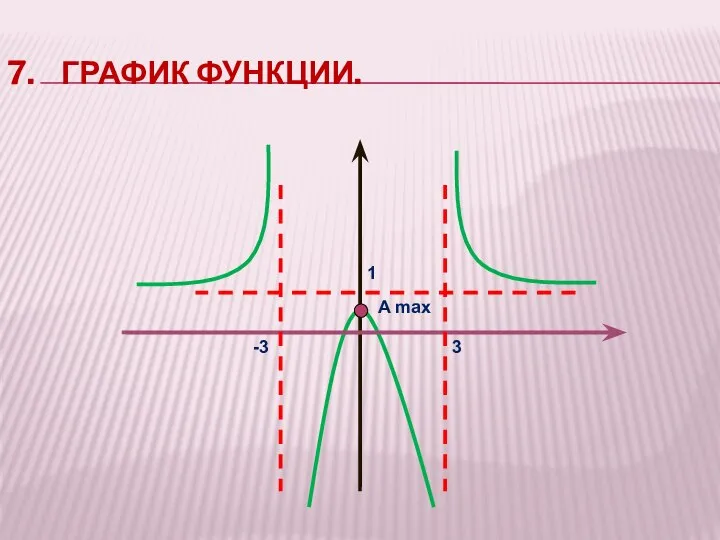
- 32. A max 7. ГРАФИК ФУНКЦИИ. -3 3 1
- 34. Скачать презентацию











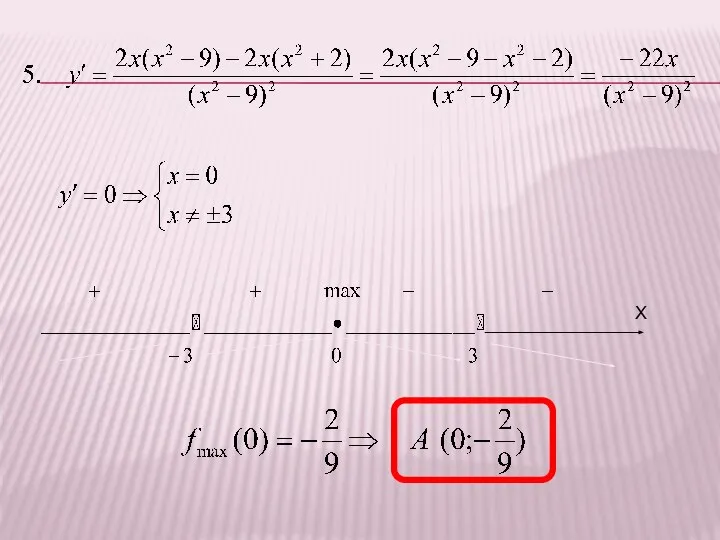
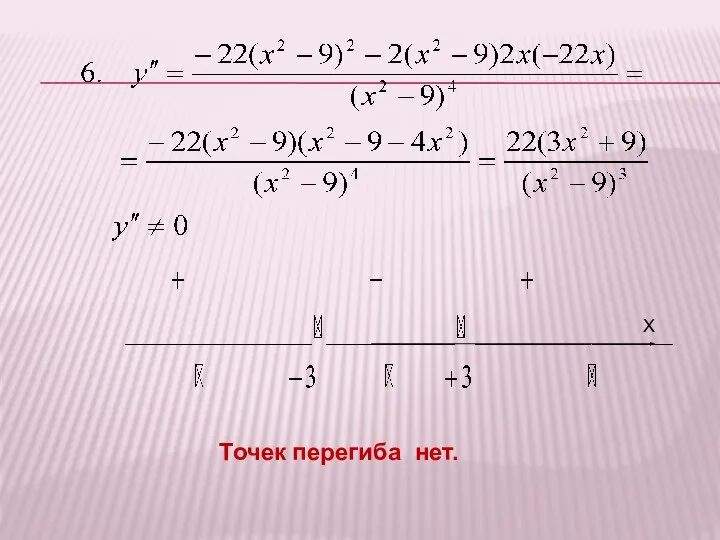
 Презентация на тему Показательная функция
Презентация на тему Показательная функция  Рисуем по координатам
Рисуем по координатам Таблица умножения пяти
Таблица умножения пяти Практическое применение производных
Практическое применение производных Эллипс
Эллипс Пропорция – верное равенство двух отношений
Пропорция – верное равенство двух отношений Сумма углов треугольника
Сумма углов треугольника Алгоритмы. Понятие и свойства алгоритмов
Алгоритмы. Понятие и свойства алгоритмов Применение производной в разных областях науки
Применение производной в разных областях науки Простейшие задачи в координатах
Простейшие задачи в координатах Запомни цифры
Запомни цифры Письменное деление на двузначное числло
Письменное деление на двузначное числло Длина. Сантиметр
Длина. Сантиметр Множества точек
Множества точек Определение и содержание математического программирования как математической дисциплины
Определение и содержание математического программирования как математической дисциплины Первообразная и интеграл
Первообразная и интеграл Лекция 1 (1)
Лекция 1 (1) Египетский треугольник
Египетский треугольник Решение логарифмических уравнений
Решение логарифмических уравнений Координаты вектора
Координаты вектора Нахождение производных функций
Нахождение производных функций Презентация на тему Простейшие задачи в координатах (9 класс)
Презентация на тему Простейшие задачи в координатах (9 класс)  Расстояние от точки до фигуры
Расстояние от точки до фигуры Решение задач
Решение задач Обоснования асимптотики для системы эллиптических уравнений в случае обратной квазимонотонности
Обоснования асимптотики для системы эллиптических уравнений в случае обратной квазимонотонности Теремок цифр. Сказка для детей 5-9 лет
Теремок цифр. Сказка для детей 5-9 лет Решение алгоритмических задач связанных с анализом графов. Использование графов деревьев, списков, при описании объектов
Решение алгоритмических задач связанных с анализом графов. Использование графов деревьев, списков, при описании объектов Повторение изученного материала. 1 класс
Повторение изученного материала. 1 класс