Содержание
- 2. Введение Каждый человек ежедневно, не всегда осознавая это решает проблему: как получить наибольший эффект, обладая ограниченными
- 3. Слово "программирование" здесь и в аналогичных терминах ("линейное программирование, динамическое программирование" и т.п.) обязано отчасти историческому
- 4. Временем рождения линейного программирования принято считать 1939 год, когда была напечатана брошюра Леонида Витальевича Канторовича "Математические
- 5. Концепции Леонида Витальевича вскоре после войны были переоткрыты на западе. Американский экономист Т. Купманс в течении
- 6. Слово SIMPLEX в обычном смысле означает простой, несоставной, в противоположность слову COMPLEX. Данный метод получил несколько
- 7. Любому набору свободных неизвестных можно придать бесчисленное множество произвольных значений, которые дадут бесчисленное множество решений. Если
- 8. Постановка задачи Рассмотрим задачу линейного программирования в виде
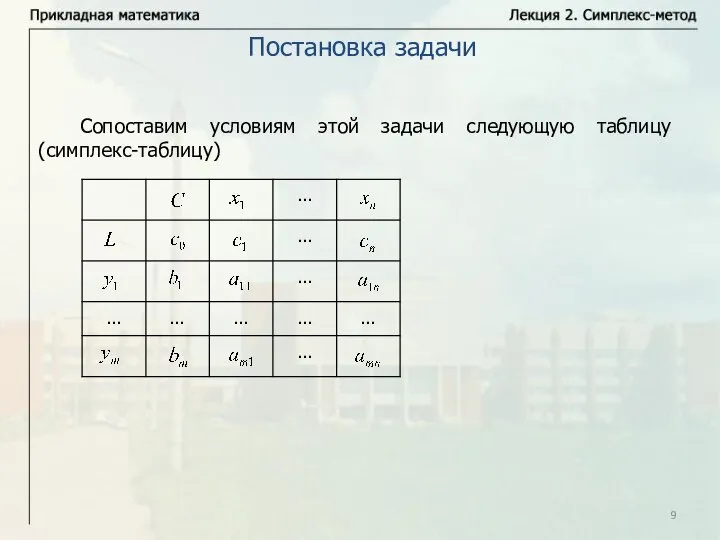
- 9. Сопоставим условиям этой задачи следующую таблицу (симплекс-таблицу) Постановка задачи
- 10. Решение задачи проводится в два этапа: 1. Нахождение опорного плана 2. Нахождение оптимального плана На первом
- 11. Правила пересчета таблицы В симплекс-таблице выделен некоторый элемент, который называется разрешающим. Этот элемент не находится в
- 12. Нахождение опорного плана Опорный план – набор значений переменных, удовлетворяющий всем ограничениям и условиям неотрицательности. Переменные
- 13. Алгоритм нахождения опорного плана 1. Если все числа первого столбца, начиная со второй строки, неотрицательны, то
- 14. 4. Рассматриваются отношения элементов первого столбца к разрешающему столбцу для всех строк, начиная со второй. Строка,
- 15. Алгоритм нахождения оптимального плана 1. Если все элементы первой строки, начиная со второго столбца, не положительны,
- 16. 4. Если таких строк нет, то . В самом деле имеется столбец вида Тогда Алгоритм нахождения
- 17. Если , то условие неотрицательности выполняется. Если , то не меняется, а если , то возрастает.
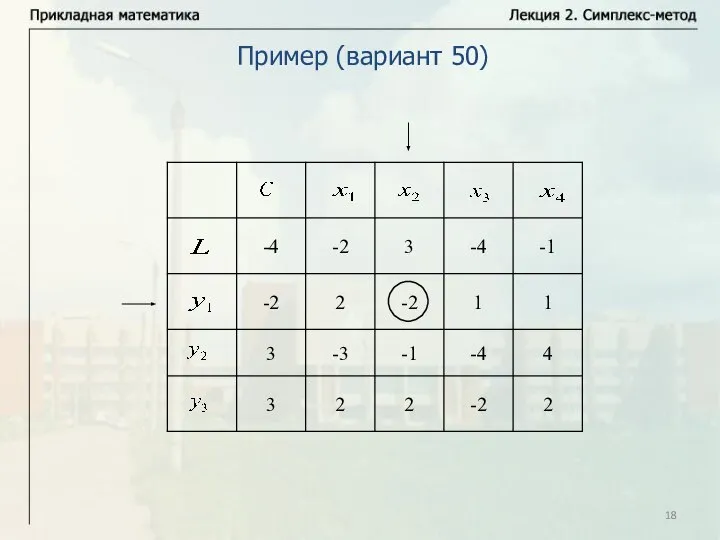
- 18. Пример (вариант 50)
- 19. Пример (вариант 50)
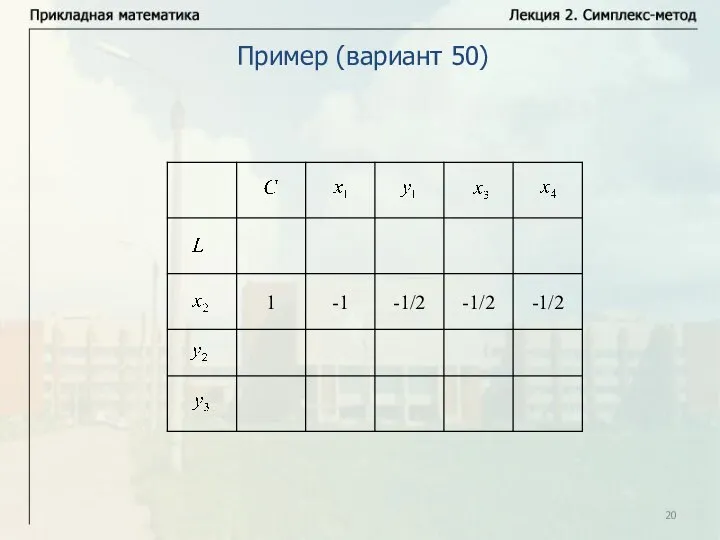
- 20. Пример (вариант 50)
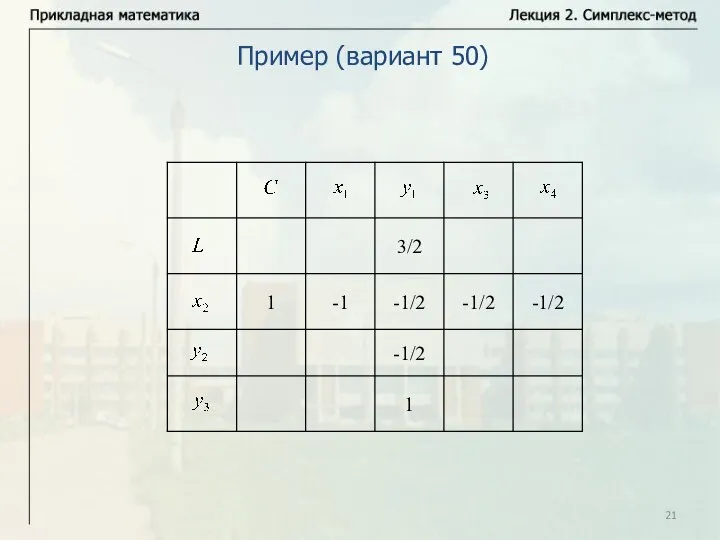
- 21. Пример (вариант 50)
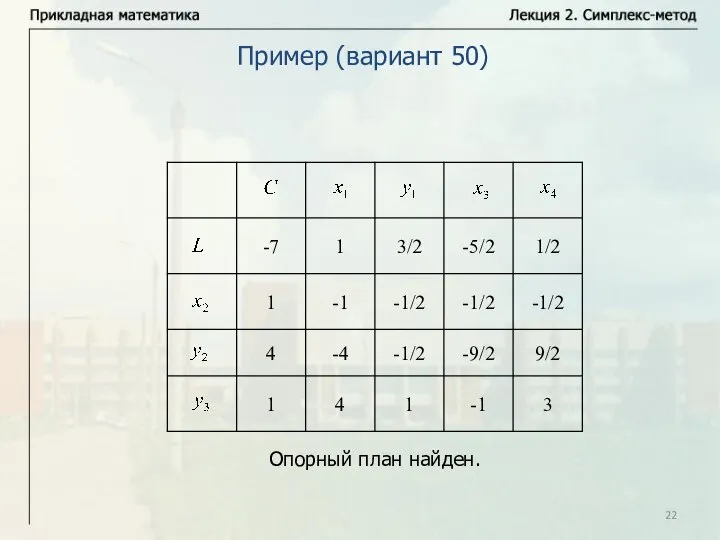
- 22. Пример (вариант 50)
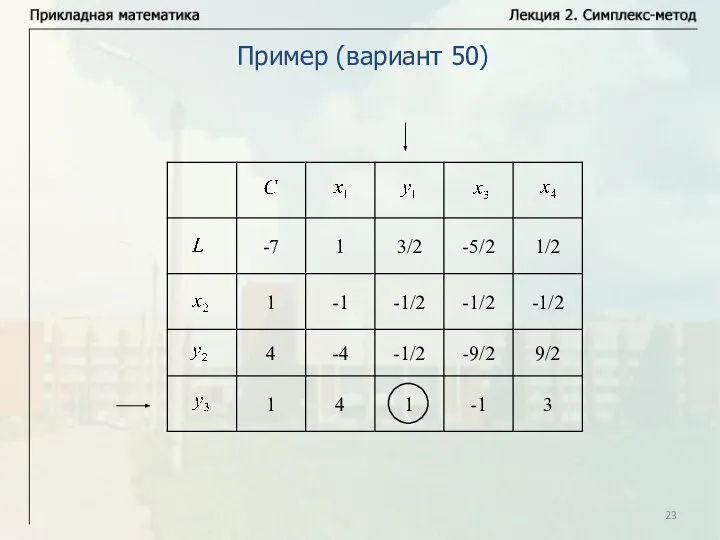
- 23. Пример (вариант 50)
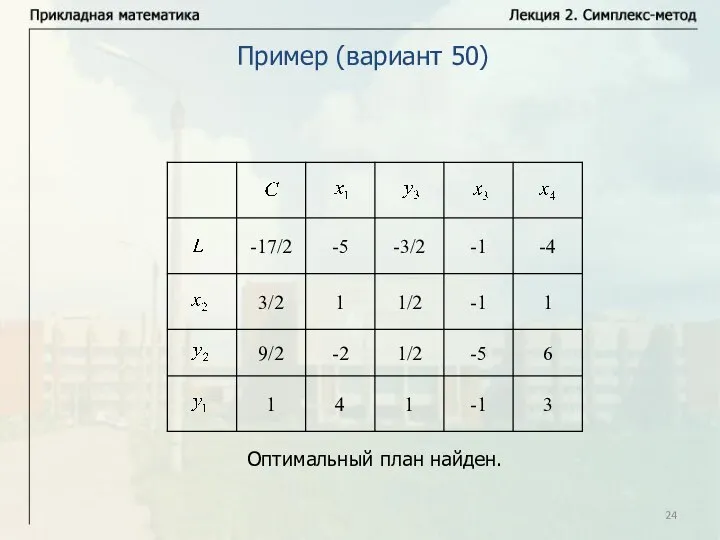
- 24. Пример (вариант 50)
- 25. Ответ: при Проверка. Найденные значения подставляются в исходную таблицу. Пример (вариант 50)
- 26. Какие переменные в симплекс-таблице являются свободными? 1) 2) 3) находящиеся в верхней строке, 4) находящиеся в
- 27. 2. Условие оптимального плана – … 1) все элементы первого столбца, начиная со второй строки, являются
- 28. 3. Какие числа в симплекс-таблице могут быть взяты в качестве разрешающих элементов? 1) -6, -5/2, -2,
- 30. Скачать презентацию




















 Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром.
Сантиметр Цель. В ходе практической работы и наблюдений познакомить учащихся 1 класса с единицей измерения длины – сантиметром. Построение сечений
Построение сечений Признаки равенства треугольников
Признаки равенства треугольников Решение систем линейных алгебраических уравнений. Тема 2
Решение систем линейных алгебраических уравнений. Тема 2 Какой многоугольник называется правильным? Приведите примеры правильных многоугольников
Какой многоугольник называется правильным? Приведите примеры правильных многоугольников Методы составления уравнений неголономной механики в задаче волнового твердотельного гироскопа
Методы составления уравнений неголономной механики в задаче волнового твердотельного гироскопа Построение сечений
Построение сечений Блок - схемы алгоритмов
Блок - схемы алгоритмов Графики
Графики Решение СЛУ
Решение СЛУ Сечение поверхностей плоскостью
Сечение поверхностей плоскостью Решение показательных уравнений. Корень уравнения
Решение показательных уравнений. Корень уравнения Пределы
Пределы Случаи сложения 470 +80 и вычитания 560-90
Случаи сложения 470 +80 и вычитания 560-90 Численные методы решения систем линейных уравнений
Численные методы решения систем линейных уравнений Комплексные корни квадратных уравнений
Комплексные корни квадратных уравнений Импорт-экспорт данных. Прикладные методы расчета и программные комплексы (5)
Импорт-экспорт данных. Прикладные методы расчета и программные комплексы (5) Геометричекие тела
Геометричекие тела Презентация на тему Математический калейдоскоп
Презентация на тему Математический калейдоскоп  Презентация на тему Умножение многочлена на многочлен
Презентация на тему Умножение многочлена на многочлен  Решение задач с пропорциональными величинами
Решение задач с пропорциональными величинами П 3
П 3 Логарифмические уравнения
Логарифмические уравнения Многогранники. Единица объема. Объем прямоугольного параллелепипеда
Многогранники. Единица объема. Объем прямоугольного параллелепипеда Функция нескольких переменных
Функция нескольких переменных Квадратичная функция
Квадратичная функция Квадратные неравенства
Квадратные неравенства Четырёхугольники. Тест
Четырёхугольники. Тест