Перпендикулярность двух плоскостей

Определение: Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 900.

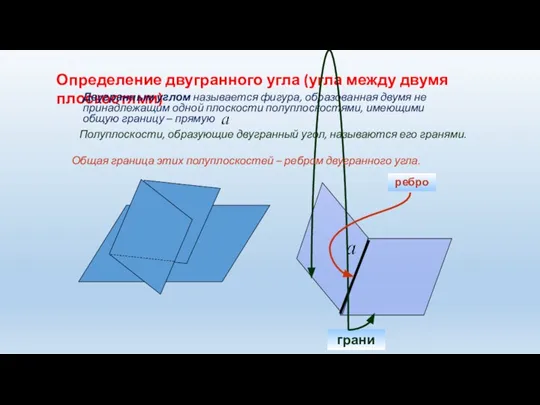
Определение двугранного угла (угла между двумя плоскостями)
Двугранным углом называется фигура, образованная двумя не принадлежащим одной плоскости полуплоскостями, имеющими общую границу – прямую .
ребро
грани
Полуплоскости, образующие двугранный угол, называются его гранями.
Общая граница этих полуплоскостей – ребром двугранного угла.

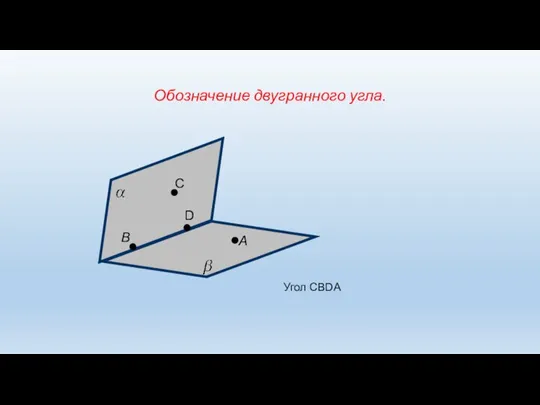
Обозначение двугранного угла.
А
В
С
D
Угол CBDA

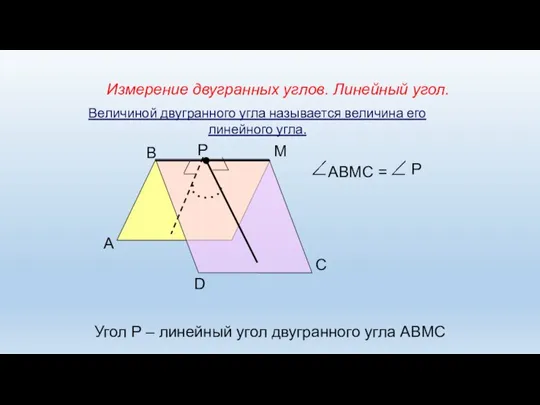
Измерение двугранных углов. Линейный угол.
А
В
М
D
Р
С
АВМС =
Р
Угол Р – линейный угол двугранного угла АВМС
Величиной двугранного угла называется величина его линейного угла.

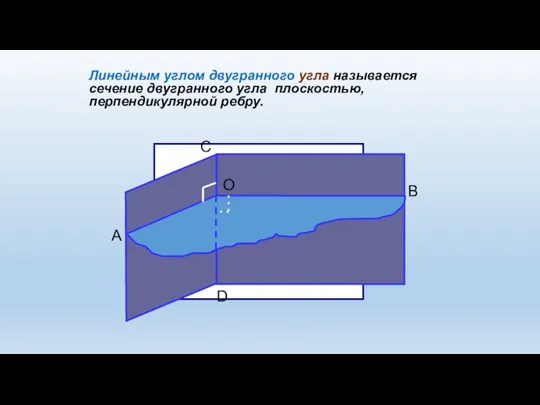
Линейным углом двугранного угла называется сечение двугранного угла плоскостью, перпендикулярной ребру.

Способ нахождения (построения) линейного угла.
1. Найти ( увидеть) ребро и грани двугранного угла
2. В гранях найти направления ( прямые) перпендикулярные ребру
3. (при необходимости) заменить выбранные направления параллельными им лучами с общим началом на ребре двугранного угла
При изображении сохраняется параллельность и отношение длин параллельных отрезков

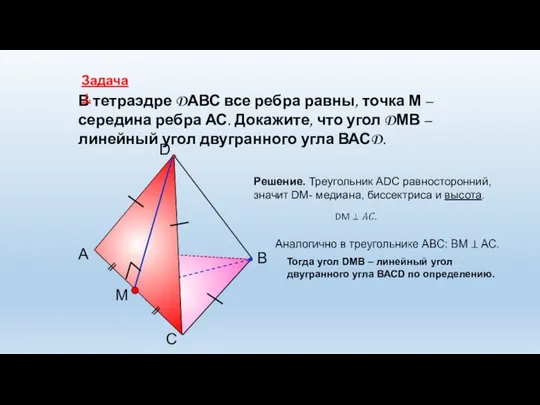
С
А
В
D
M
В тетраэдре DАВС все ребра равны, точка М – середина ребра АС. Докажите, что угол DМВ – линейный угол двугранного угла ВАСD.
Задача 1.
Решение. Треугольник ADC равносторонний,
значит DM- медиана, биссектриса и высота.
Тогда угол DМВ – линейный угол
двугранного угла ВАСD по определению.

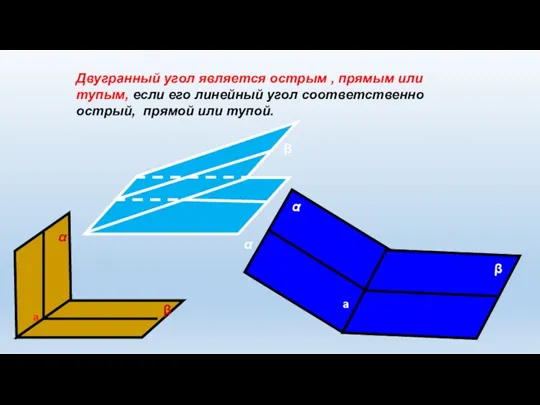
Двугранный угол является острым , прямым или тупым, если его линейный угол соответственно острый, прямой или тупой.
α
β

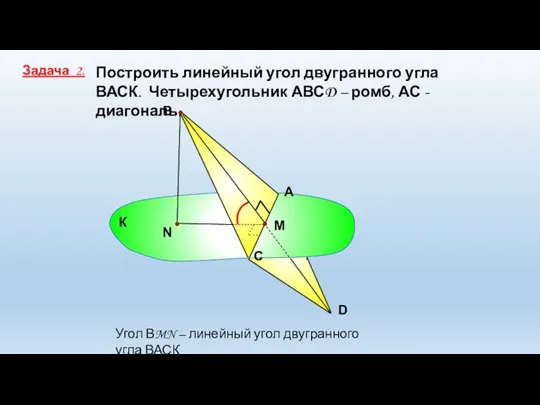
Построить линейный угол двугранного угла ВАСК. Четырехугольник АВСD – ромб, АС - диагональ.
А
С
В
Угол ВMN – линейный угол двугранного угла ВАСК
К
D
Задача 2.

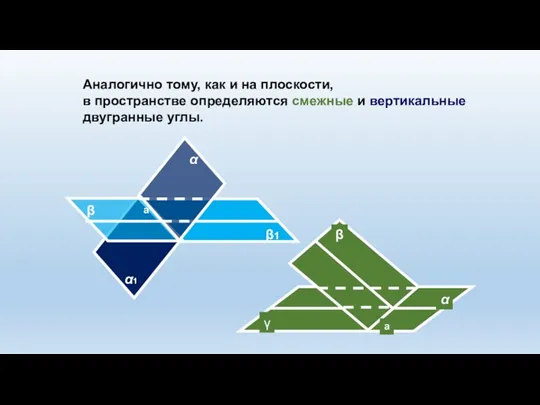
Аналогично тому, как и на плоскости,
в пространстве определяются смежные и вертикальные двугранные углы.
β
β1
а
α
α1

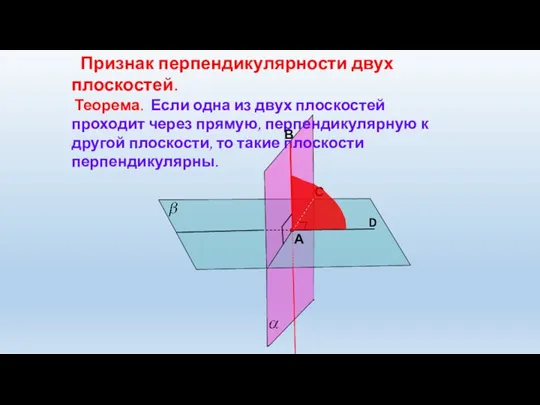
Признак перпендикулярности двух плоскостей.
Теорема. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
А
С

Другой рисунок.
Если плоскость β проходит через прямую АВ, перпендикулярную к плоскости α, то β α
А

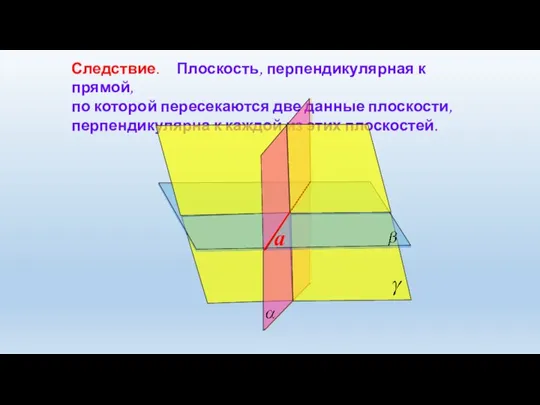
Следствие. Плоскость, перпендикулярная к прямой,
по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.

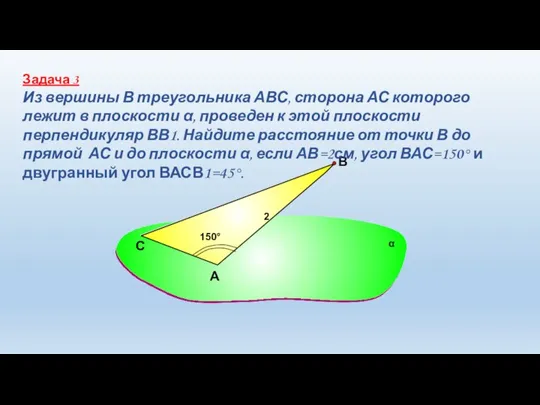
А
В
Задача 3
Из вершины В треугольника АВС, сторона АС которого лежит в плоскости α, проведен к этой плоскости перпендикуляр ВВ1. Найдите расстояние от точки В до прямой АС и до плоскости α, если АВ=2см, угол ВАС=150° и двугранный угол ВАСВ1=45°.
С
2
α
150°

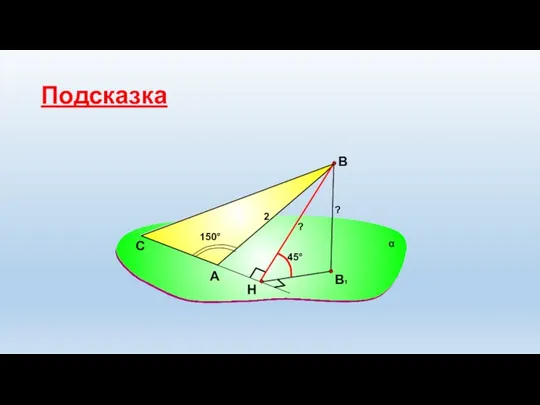
А
В
С
2
α
45°
150°
?
?
Подсказка