Слайд 2Категориальные переменные
Принимают конечное, но большее двух множество значений
Например, переменная education – принимает

значение:
1 - для индивидов с незаконченным средним образованием;
2 – для индивидов с законченным средним образованием;
3 – для индивидов с незаконченным высшим образованием;
4 – для индивидов с законченным высшим образованием;
5 – для закончивших аспирантуру.
Слайд 3Например, переменная trustgovernment – принимает значение:
1 – если индивид полностью доверяет правительству;
2

– если скорее доверяет;
3 – если относится нейтрально;
4 – если скорее не доверяет;
5 – если совсем не доверяет.
Слайд 4Например, переменная fedokrug– федеральный округ, в котором проживает индивид, принимает значение:
1 –

для Северо-Западного ФО ;
2 – для Центрального ФО;
3 – для Южного ФО;
4 – для Сибирского ФО;
5 – для Уральского ФО
6 – для Приволжского ФО
7 – для Дальневлсточного ФО
8 – для Северо-Кавказского ФО
9 – для Крымского ФО.
Слайд 5Категориальные переменные не рекомендуется включать в уравнение регрессии в первоначальном виде.
Вместо одной

категориальной в уравнение регрессии включается набор фиктивных переменных
При этом (важно!!!) фиктивных переменных в уравнение регрессии следует включать на одну меньше, чем выделено категорий.
Невключенная категория называется базовой и все остальные категории сравниваются с ней.
Слайд 6Например, при моделировании зависимости спроса на некоторый товар Y от его цены

Р и среднего дохода покупателей I нередко возникает необходимость учитывать сезонность. Пусть данные являются квартальными, тогда можно создать 4 дополнительные дамми-переменные:
D1, которая =1 если период наблюдения первый квартал, и =0, если период наблюдения 2, 3 или 4 кварталы;
D2, которая =1 если период наблюдения второй квартал, и =0, если период наблюдения 1, 3 или 4 кварталы;
D3, которая =1 если период наблюдения третий квартал, и =0, если период наблюдения 1, 2 или 4 кварталы;
D4, которая =1 если период наблюдения четвертый квартал, и =0, если период наблюдения 1, 2 или 3 кварталы;
Слайд 7Но в уравнение регрессии следует включать не все 4, а только 3

квартальные дамми-переменные.
Это объясняется тем, что дамми-переменные D1, D2,D3 и D4 в сумме дают единичный столбец, и тогда условие теоремы Гаусса-Маркова о независимости столбцов матрицы Х будет нарушено (возникнет мультиколлинеарность).
Слайд 8Если в примере с сезонностью в качестве базового выбран первый квартал, то

уравнение регрессии имеет вид
Оцененное уравнение регрессии
Для 1-го квартала
Для 2-го квартала
Для 3-го квартала
Для 4-го квартала
Слайд 9Интерпретация коэффициентов:
Если коэффициент значим, то разница в спросе в первом и

втором кварталах составляет . Аналогично значимость
отражает разницу в спросе в первом и третьем (четвертом) квартале
Слайд 10Пример
Имеются данные о цвете (Color), длине (Length), ширине (Width) лепестков и показателе

роста цветков (Rate).









 Знакомство с подсчётом вероятности
Знакомство с подсчётом вероятности Тест. Равенство треугольников
Тест. Равенство треугольников Логарифм числа
Логарифм числа Презентация по математике "Сложение и вычитание в пределах 1000" -
Презентация по математике "Сложение и вычитание в пределах 1000" -  Презентация на тему МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Презентация на тему МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ  Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Сложение с числом 10
Сложение с числом 10 Линейная корреляция
Линейная корреляция Проецирование – это процесс получения
Проецирование – это процесс получения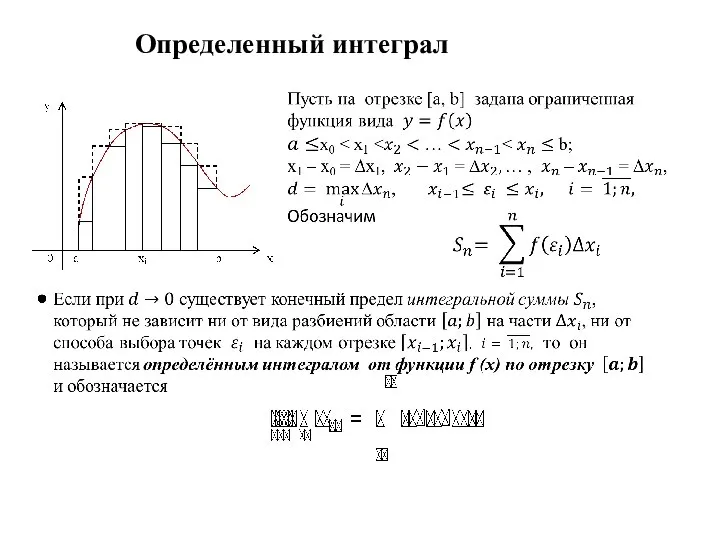 Определённый интеграл
Определённый интеграл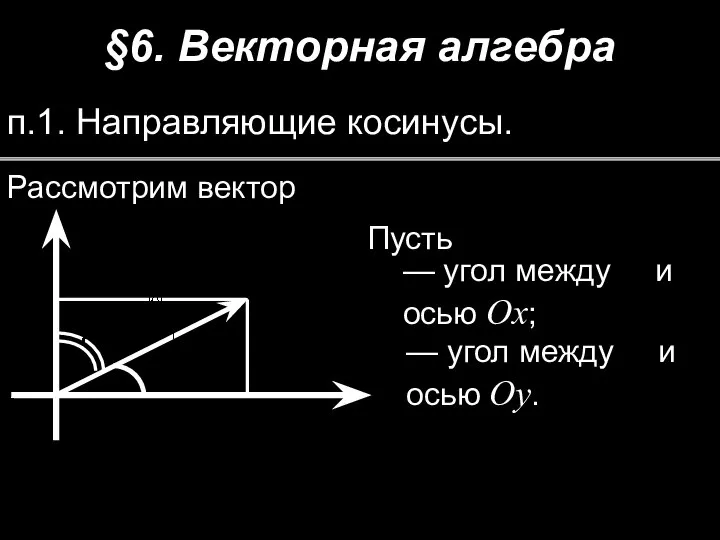 2.3. Векторная алгебра
2.3. Векторная алгебра Признаки параллельности прямых
Признаки параллельности прямых Решение задач. Урок математики
Решение задач. Урок математики Сложение вида + 1, вычитание вида -1
Сложение вида + 1, вычитание вида -1 Подготовка к ЕГЭ
Подготовка к ЕГЭ Цифры - прописи. Анимированный плакат
Цифры - прописи. Анимированный плакат Лекция 5. Трехмерные преобразования
Лекция 5. Трехмерные преобразования Кратные чисел. 5 класс
Кратные чисел. 5 класс 2020.09.03 Десятичная система записи натуральных чисел
2020.09.03 Десятичная система записи натуральных чисел Pervoobraznaya
Pervoobraznaya Итоговой тест по геометрии. 9 класс
Итоговой тест по геометрии. 9 класс Приведение уравнений фигур к каноническому виду при помощи квадратичных форм
Приведение уравнений фигур к каноническому виду при помощи квадратичных форм Решение треугольников
Решение треугольников Треугольник. Виды треугольников
Треугольник. Виды треугольников Моделирование вероятности столкновения судов
Моделирование вероятности столкновения судов Сплайн интерполяция. Отчёт по домашней работе №3
Сплайн интерполяция. Отчёт по домашней работе №3 Иррациональные числа
Иррациональные числа Тест 3 по математике
Тест 3 по математике