Содержание
- 2. Пахомова Наталья Алексеевна
- 3. История возникновения 1885г. Фредерик Тейлор – вывод о возможности применения научного анализа в сфере производства. 1916г.
- 4. Методы оптимальных решений рассматривают следующие задачи: Задачи управления запасами Задачи распределения ресурсов Задачи ремонта и замены
- 5. Оптимальное математическое программирование ЦЕЛЬ (критерий, целевая функция) F(x1;x2;…;xn) → экстремум ОГРАНИЧЕНИЯ (условия, требования) Gj(x1;x2;…;xn) [>;≥;=; ТРЕБОВАНИЯ
- 6. Полное решение поставленной задачи не найдено, но получены существенные результаты во множестве частных случаев Если функции
- 7. История линейного программирования КАНТОРОВИЧ Леонид Витальевич (1912-86), российский математик и экономист, академик АН СССР. Положил начало
- 8. Задача линейного программирования имеет следующий вид 1) Целевая функция Z= → экстремум (оптимум) 2) Ограничения [>≥=
- 9. СПОСОБЫ РЕШЕНИЯ ЛИНЕЙНЫХ ЗАДАЧ Графический способ Средствами Excel (Поиск решения) Средствами MathCAD (функция Minimize) Способ Жордановых
- 10. Пример:
- 11. Графический способ
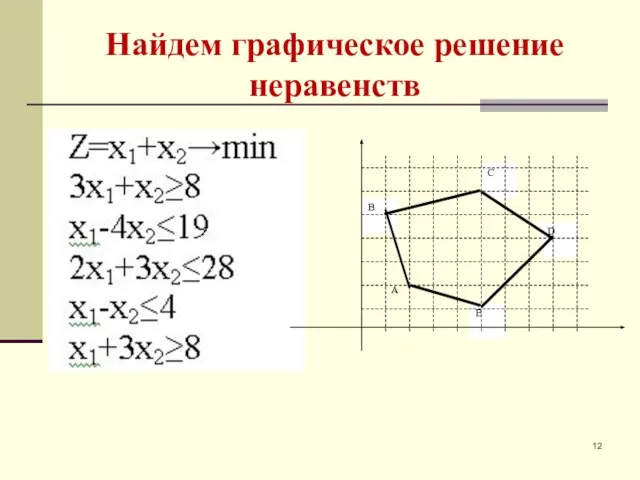
- 12. Найдем графическое решение неравенств
- 13. Графиком целевой функции является семейство параллельных прямых
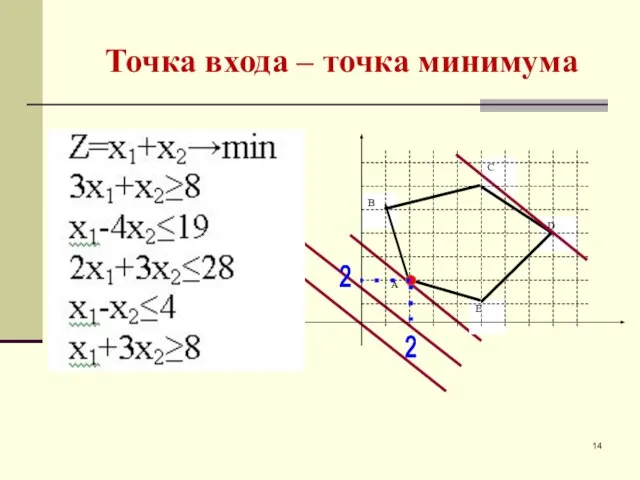
- 14. Точка входа – точка минимума 2 2
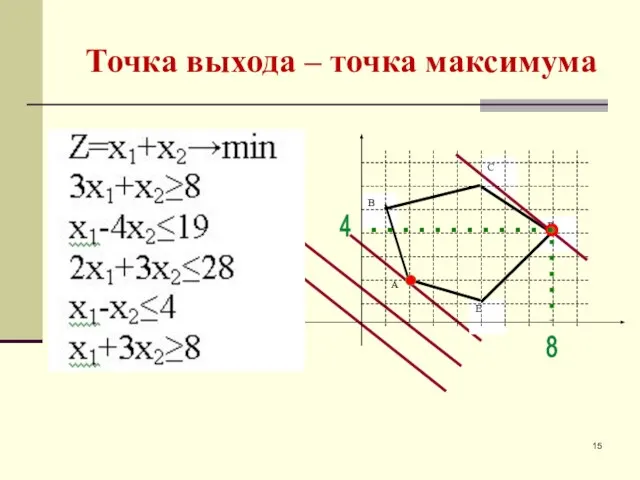
- 15. Точка выхода – точка максимума 8 4
- 16. СПОСОБ ЖОРДАНОВЫХ ИСКЛЮЧЕНИЙ (СИМПЛЕКСНЫЙ) Симплексный метод требует преобразования имеющейся модели к каноническому виду. каждое неравенство должно
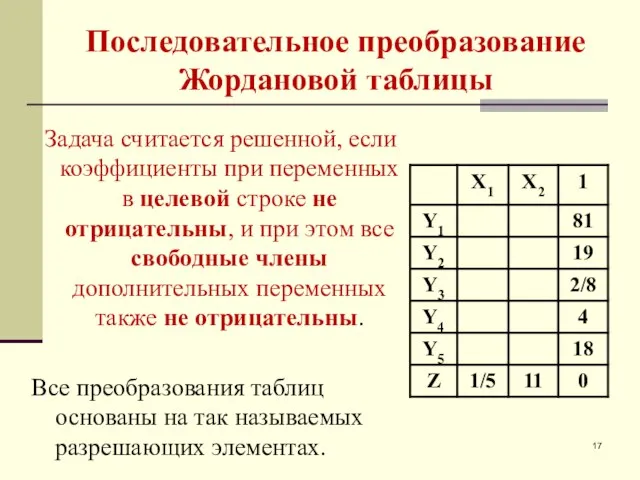
- 17. Последовательное преобразование Жордановой таблицы Задача считается решенной, если коэффициенты при переменных в целевой строке не отрицательны,
- 18. Правила выбора разрешающего элемента Разрешающий элемент не может находиться в столбце свободных членов и в строке
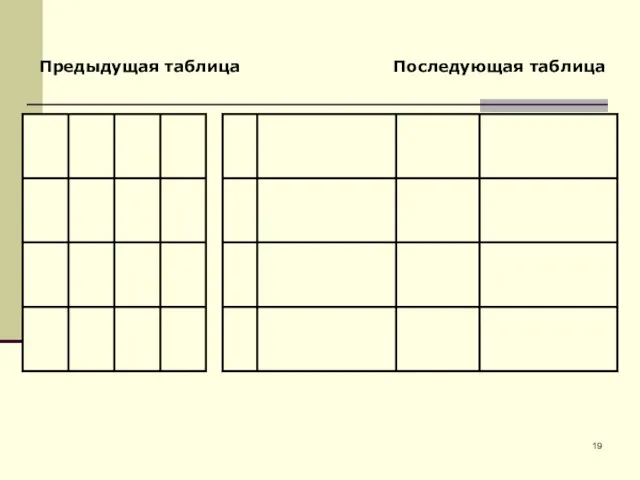
- 19. Предыдущая таблица Последующая таблица
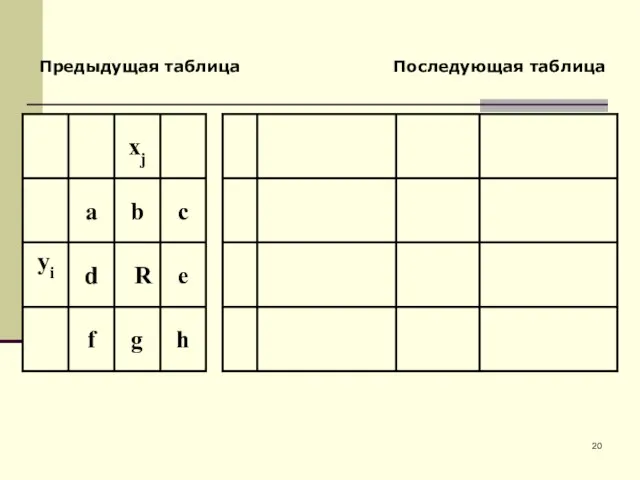
- 20. Предыдущая таблица Последующая таблица
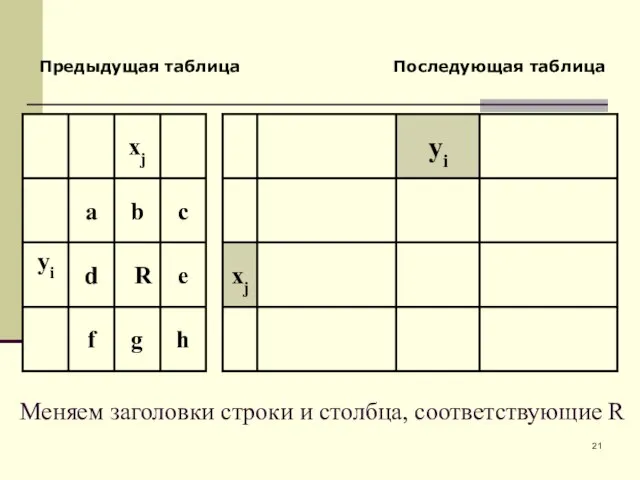
- 21. Предыдущая таблица Последующая таблица Меняем заголовки строки и столбца, соответствующие R
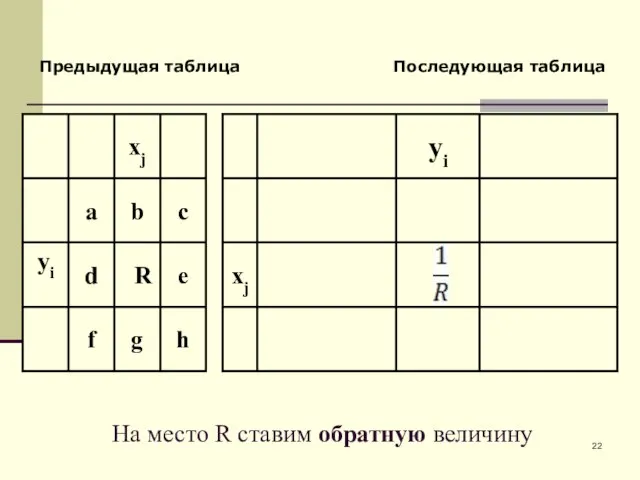
- 22. Предыдущая таблица Последующая таблица На место R ставим обратную величину
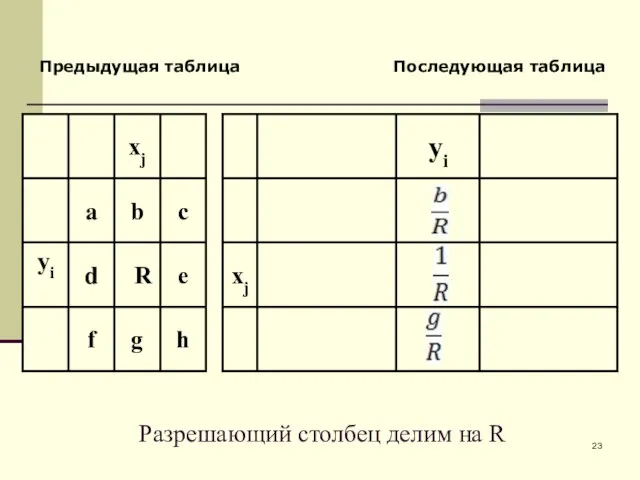
- 23. Предыдущая таблица Последующая таблица Разрешающий столбец делим на R
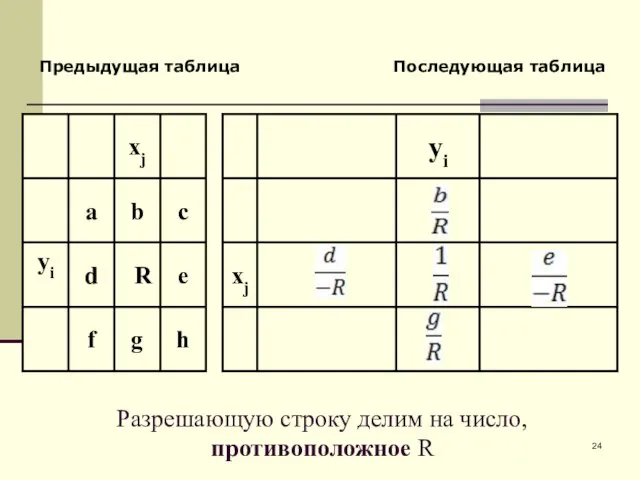
- 24. Предыдущая таблица Последующая таблица Разрешающую строку делим на число, противоположное R
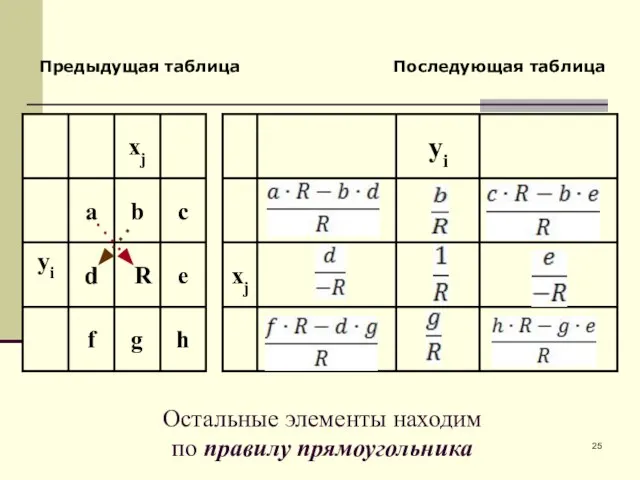
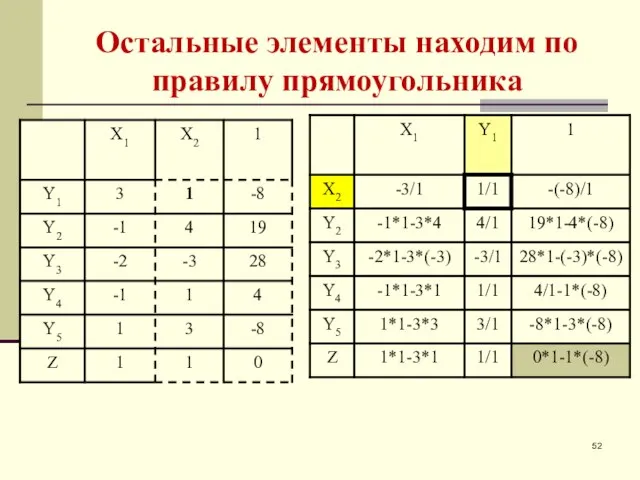
- 25. Предыдущая таблица Последующая таблица Остальные элементы находим по правилу прямоугольника
- 26. Основная форма представления задачи линейного программирования Исходная форма Каноническая форма Z=x1+x2→min Z=x1+x2→min 3x1+x2≥8 y1=3x1+x2-8 x1-4x2≤19 y2=-x1-
- 27. Основная форма представления задачи линейного программирования Исходная форма Каноническая форма Z=x1+x2→min Z=x1+x2→min 3x1+x2≥8 y13x1 + x2-
- 28. Исходная форма Каноническая форма Z=x1+x2→min Z=x1+x2→min 3x1+x2≥8 y1 3x1+ x2-8 ≥0 x1-4x2≤19 y2 -x1+4x2+19 ≥0 2x1+3x2≤28
- 29. Исходная форма Каноническая форма Z=x1+x2→min Z=x1+x2→min 3x1+x2≥8 y1=3x1+x2 ─ 8 x1-4x2≤19 y2= ─ x1+4x2+19 2x1+3x2≤28 y3=
- 30. Все коэффициенты канонической формы заносят в Жорданову таблицу В заголовках столбцов этой таблицы ставят имена определяемых
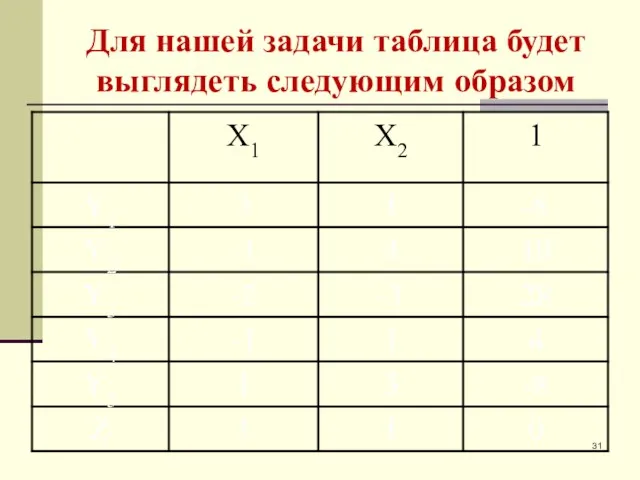
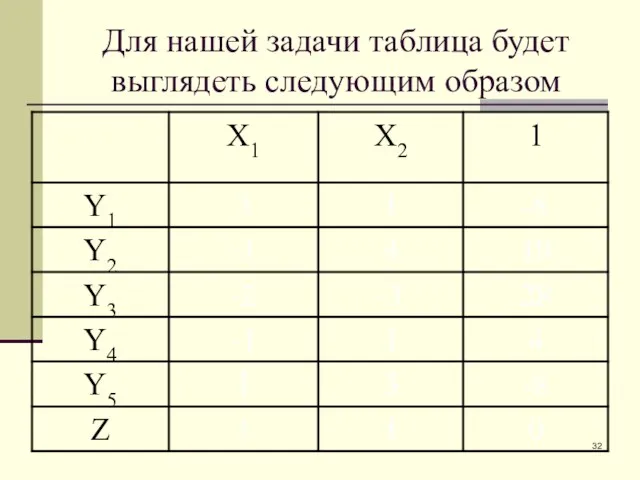
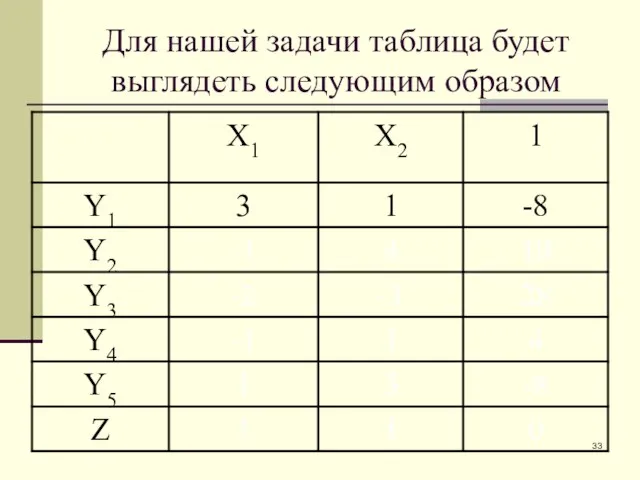
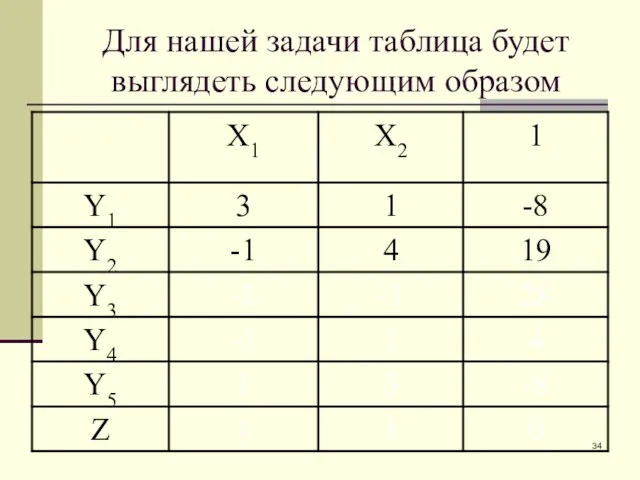
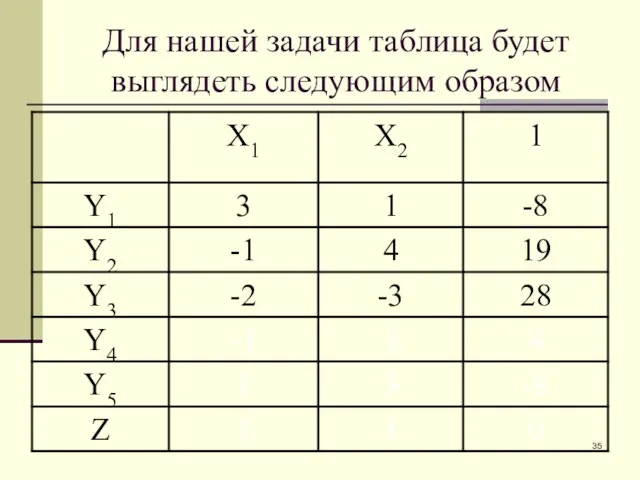
- 31. Для нашей задачи таблица будет выглядеть следующим образом
- 32. Для нашей задачи таблица будет выглядеть следующим образом
- 33. Для нашей задачи таблица будет выглядеть следующим образом
- 34. Для нашей задачи таблица будет выглядеть следующим образом
- 35. Для нашей задачи таблица будет выглядеть следующим образом
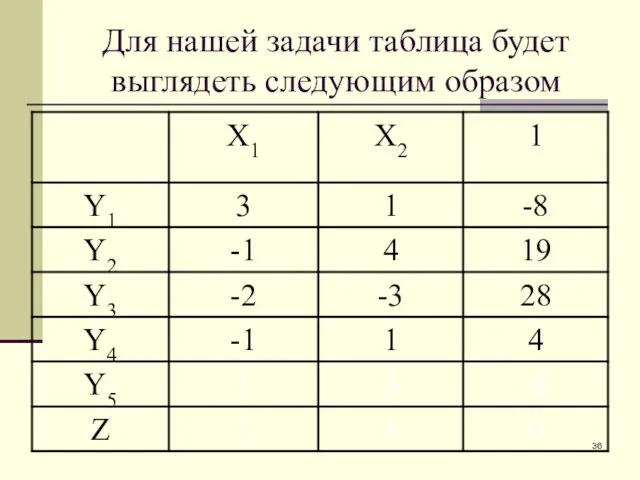
- 36. Для нашей задачи таблица будет выглядеть следующим образом
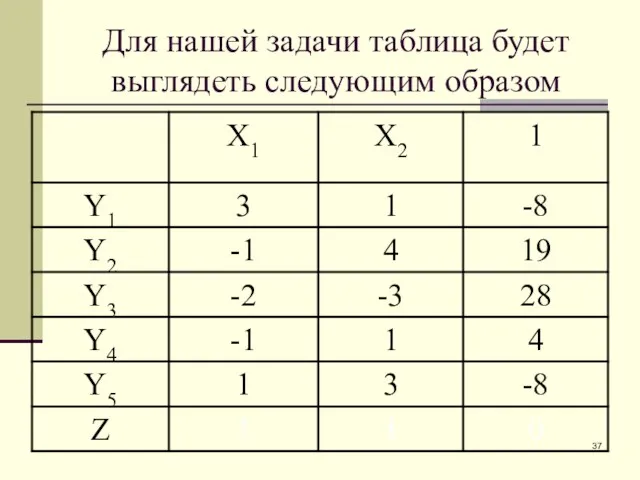
- 37. Для нашей задачи таблица будет выглядеть следующим образом
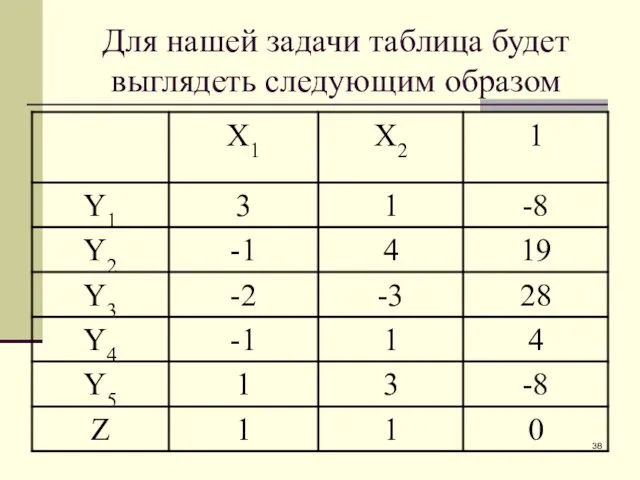
- 38. Для нашей задачи таблица будет выглядеть следующим образом
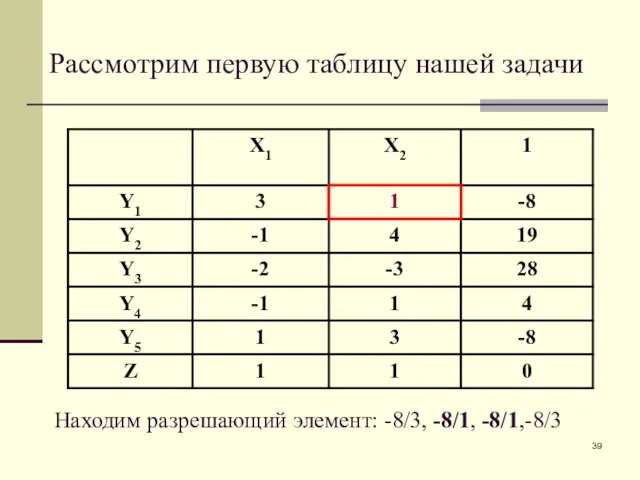
- 39. Рассмотрим первую таблицу нашей задачи Находим разрешающий элемент: -8/3, -8/1, -8/1,-8/3
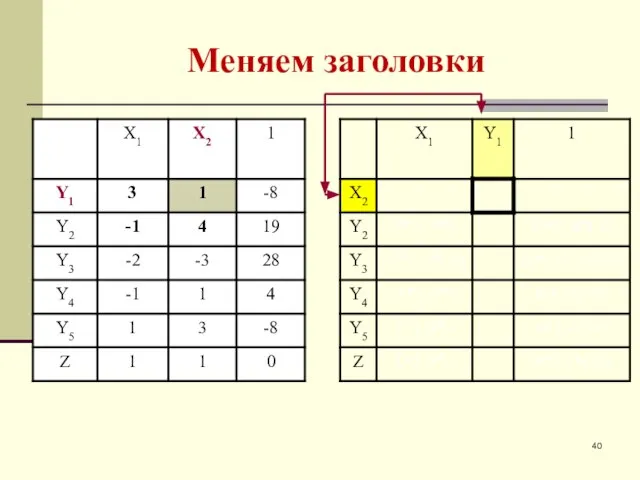
- 40. Меняем заголовки
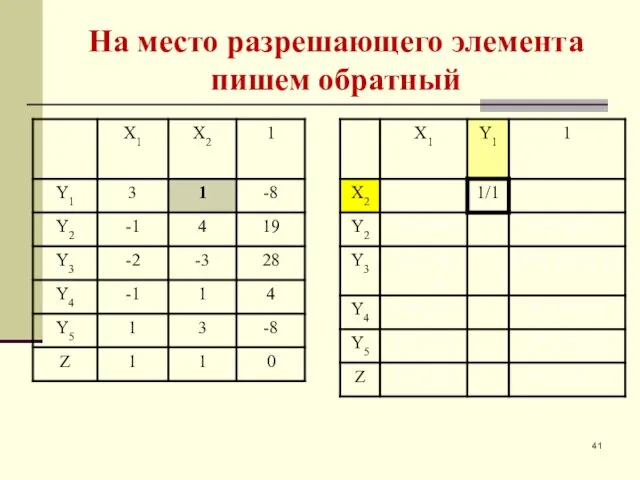
- 41. На место разрешающего элемента пишем обратный
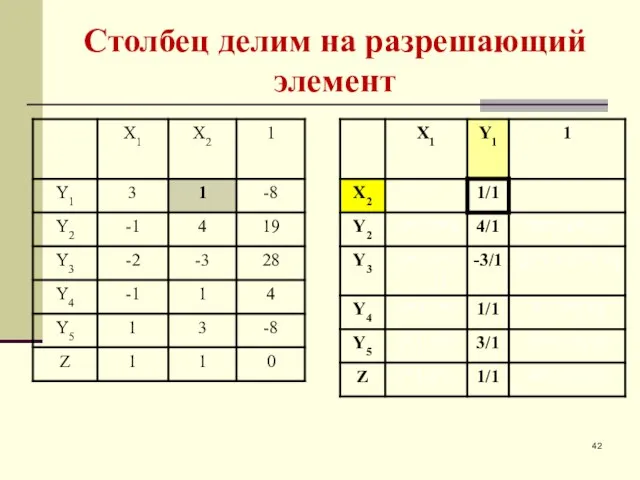
- 42. Столбец делим на разрешающий элемент
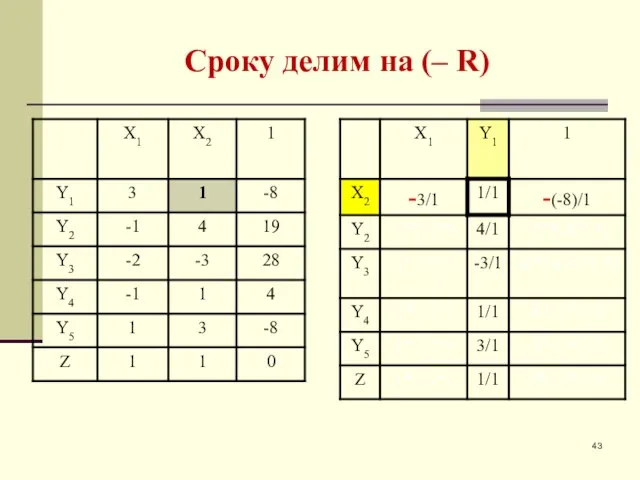
- 43. Сроку делим на (– R)
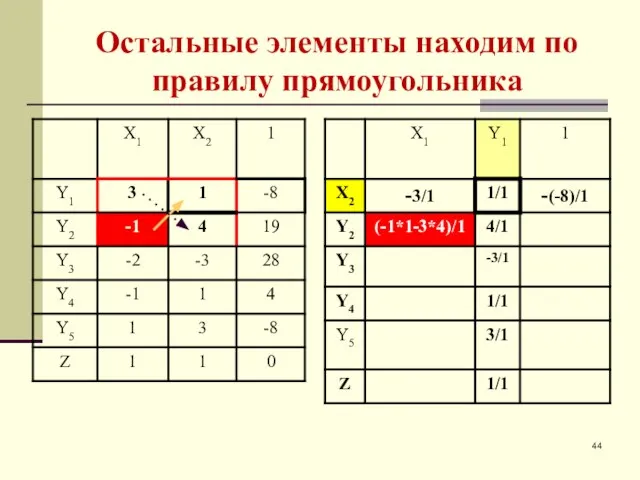
- 44. Остальные элементы находим по правилу прямоугольника
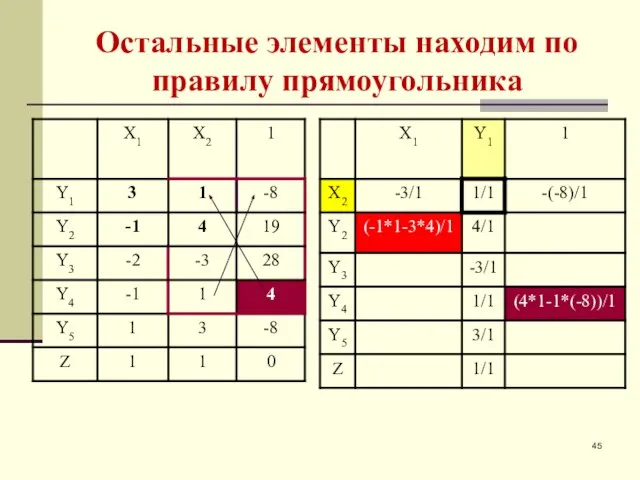
- 45. Остальные элементы находим по правилу прямоугольника
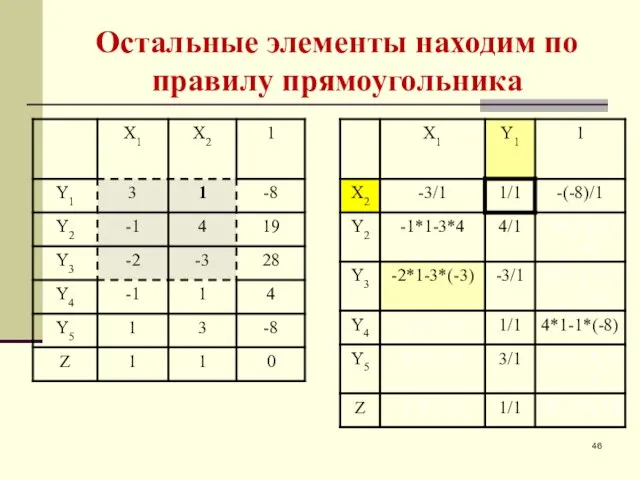
- 46. Остальные элементы находим по правилу прямоугольника
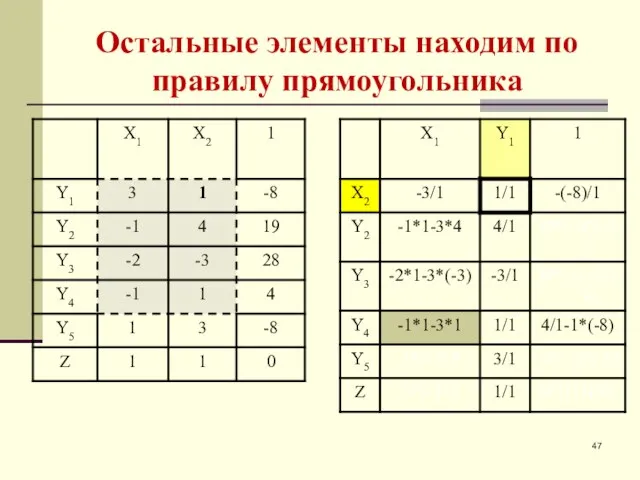
- 47. Остальные элементы находим по правилу прямоугольника
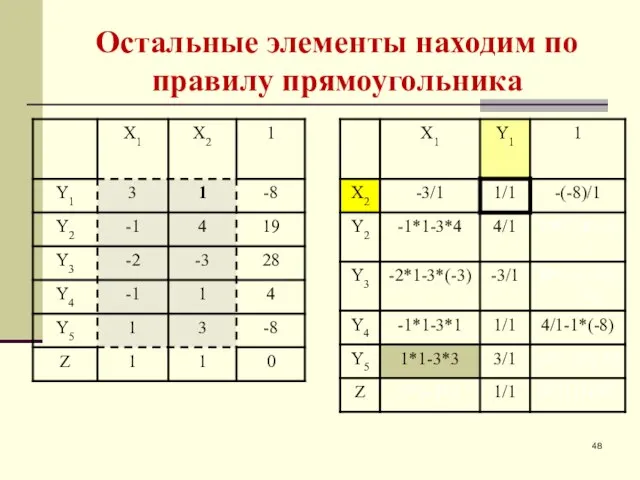
- 48. Остальные элементы находим по правилу прямоугольника
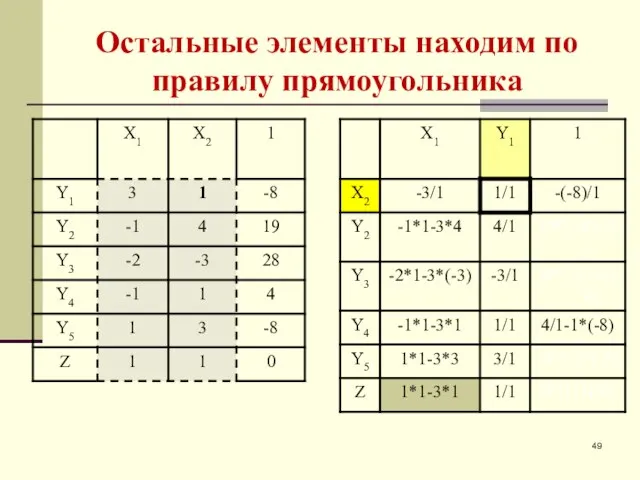
- 49. Остальные элементы находим по правилу прямоугольника
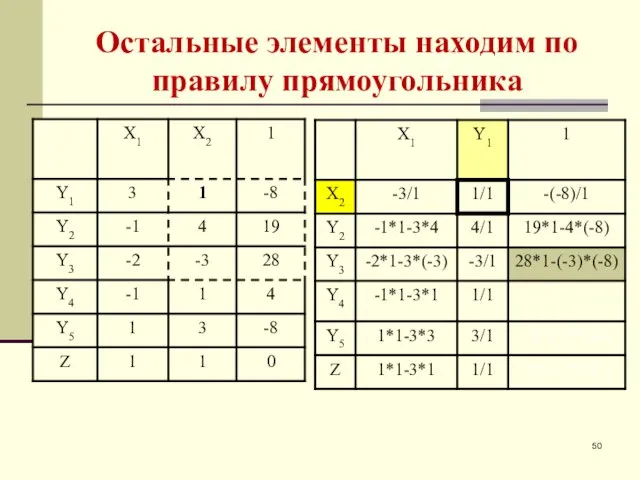
- 50. Остальные элементы находим по правилу прямоугольника
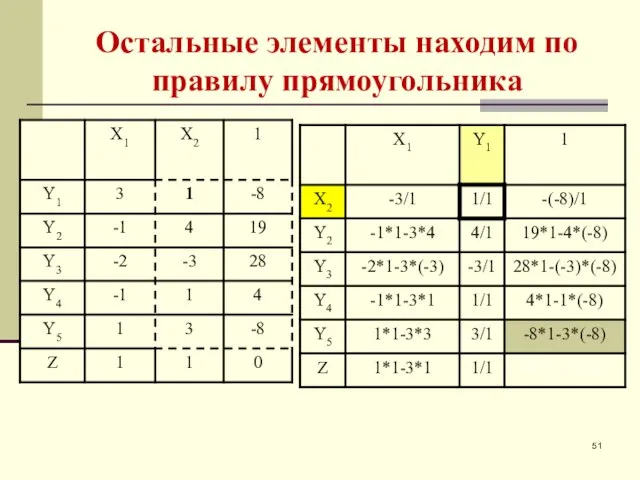
- 51. Остальные элементы находим по правилу прямоугольника
- 52. Остальные элементы находим по правилу прямоугольника
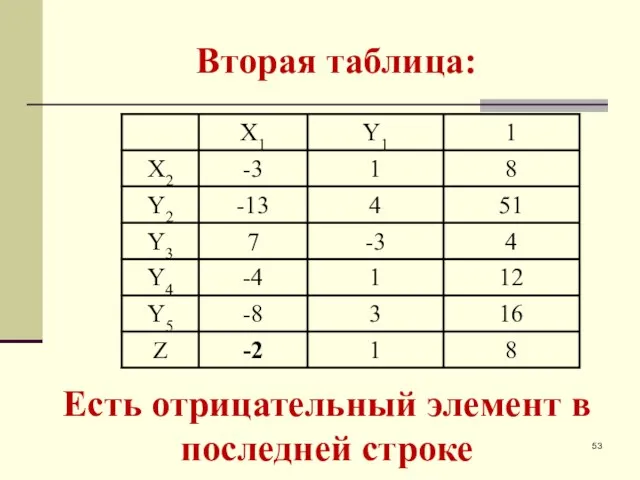
- 53. Вторая таблица: Есть отрицательный элемент в последней строке
- 54. -8/3 Наибольшее из всех возможных отношений соответствующих свободных членов к отрицательным элементам такого столбца
- 55. -51/13, -8/3 Наибольшее из всех возможных отношений соответствующих свободных членов к отрицательным элементам такого столбца
- 56. -12/4, -51/13, -8/3 Наибольшее из всех возможных отношений соответствующих свободных членов к отрицательным элементам такого столбца
- 57. -16/8, -12/4, -51/13, -8/3; наибольшее число -16/8=-2 Наибольшее из всех возможных отношений соответствующих свободных членов к
- 58. Разрешающий элемент (– 8 )
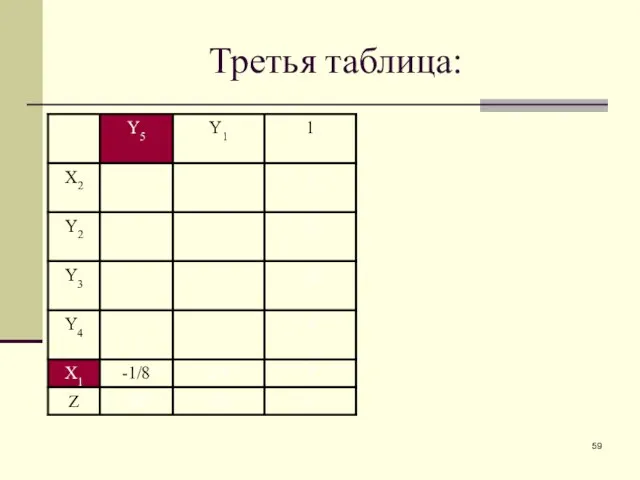
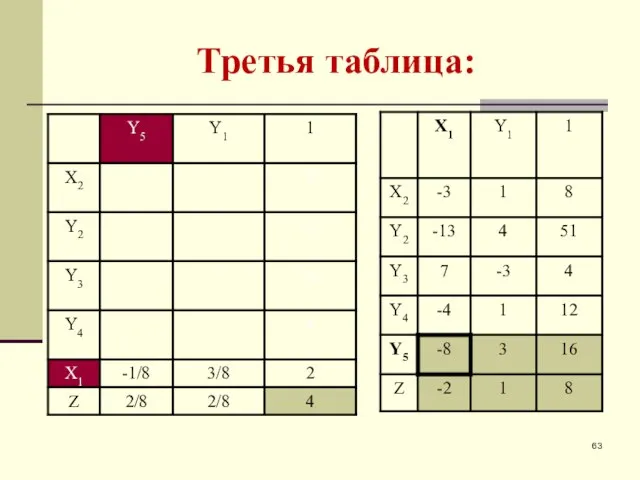
- 59. Третья таблица:
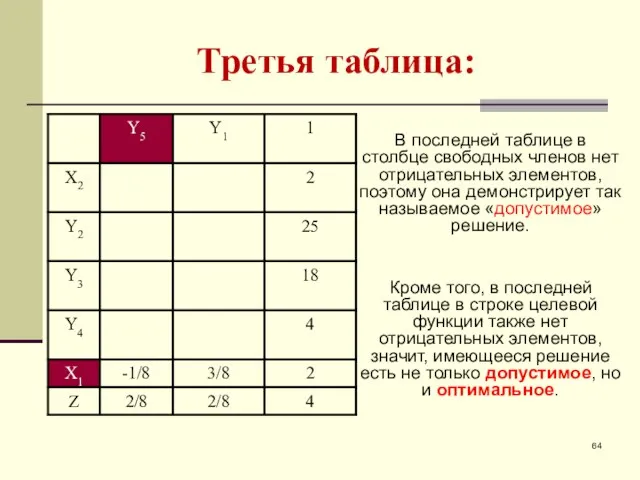
- 60. Третья таблица: В последней таблице в столбце свободных членов нет отрицательных элементов, поэтому она демонстрирует так
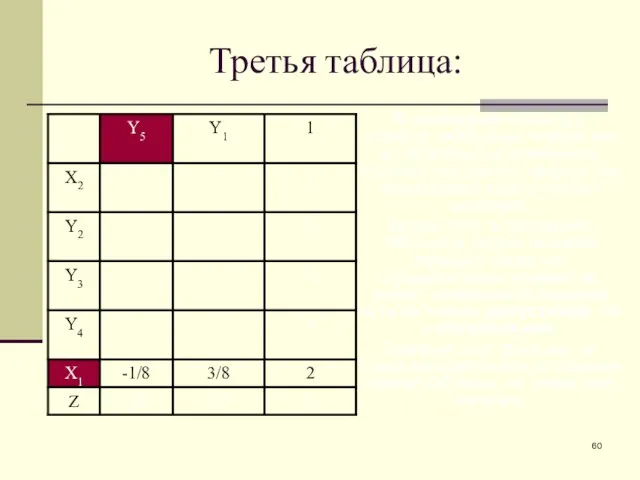
- 61. Третья таблица: В последней таблице в столбце свободных членов нет отрицательных элементов, поэтому она демонстрирует так
- 62. Третья таблица: ( 1* (-8) - 3* (-2))/(-8) = (-8+6)/(-8)= - 2/( - 8) = 2/8
- 63. Третья таблица:
- 64. Третья таблица: В последней таблице в столбце свободных членов нет отрицательных элементов, поэтому она демонстрирует так
- 65. Оформление результата решения Результат решения определяют из последней таблицы следующим образом: переменная, стоящая в заголовке строки
- 66. Проверка: 3*2+2=8, 8=8, различия левой и правой частей нет, значит Y1=0, и в последней таблице Y1
- 67. Решение задач линейного программирования в Excel В настоящее время наиболее мощным средством решения таких задач на
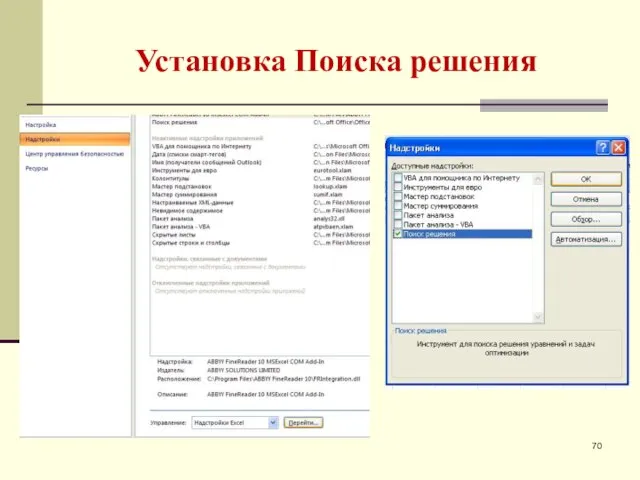
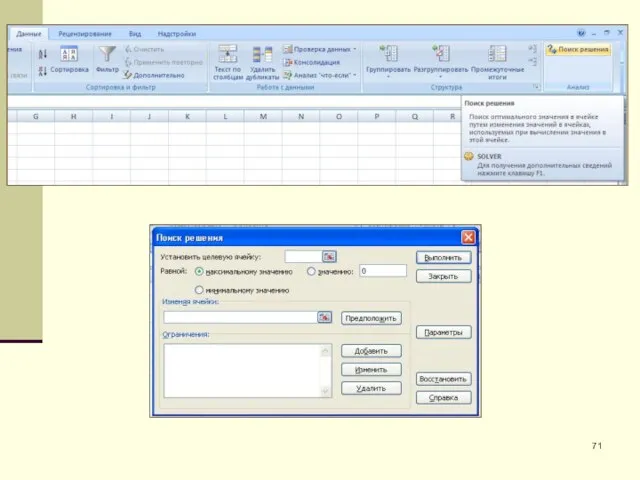
- 68. Установка Поиска решения
- 69. Установка Поиска решения
- 70. Установка Поиска решения
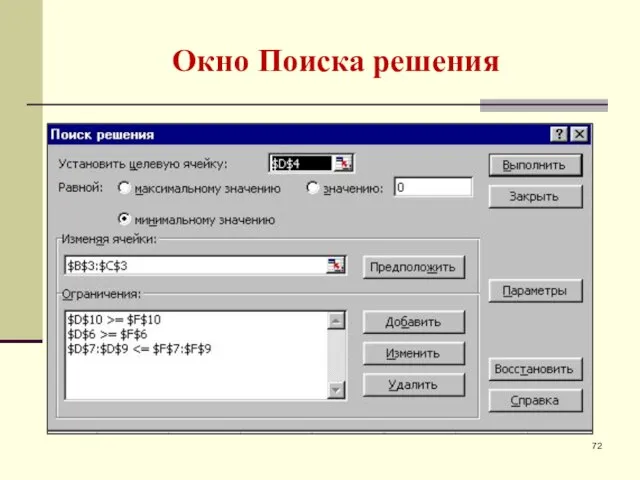
- 72. Окно Поиска решения
- 74. Скачать презентацию




























 Функции многих переменных. Лекция 16
Функции многих переменных. Лекция 16 Выдающиеся российские математики. Урок-лекция, 5- 11 кл
Выдающиеся российские математики. Урок-лекция, 5- 11 кл Тригонометрия. Математика с Д.А. Власовым
Тригонометрия. Математика с Д.А. Власовым Центральная и осевая симметрия
Центральная и осевая симметрия Единицы стоимости. Рубль, копейка
Единицы стоимости. Рубль, копейка Умножение десятичной дроби на натуральное число. Графический диктант
Умножение десятичной дроби на натуральное число. Графический диктант Тригонометрические функции
Тригонометрические функции Презентация по математике. Исторические сведения
Презентация по математике. Исторические сведения Линейная регрессия
Линейная регрессия Презентация на тему Прямоугольный параллелепипед. Куб
Презентация на тему Прямоугольный параллелепипед. Куб  Отбор корней в тригонометрическом уравнении
Отбор корней в тригонометрическом уравнении Предел функции в точке и на бесконечности
Предел функции в точке и на бесконечности Элементы линейной алгебры. Матрицы. Определители
Элементы линейной алгебры. Матрицы. Определители Предел функции (часть 2)
Предел функции (часть 2) Пирамида. Определение пирамиды. Виды пирамид
Пирамида. Определение пирамиды. Виды пирамид Теорема Пифагора
Теорема Пифагора Старинные задачки по математике
Старинные задачки по математике Простейшие преобразования графиков
Простейшие преобразования графиков Инструкция по изготовлению трубогранника. Тетраэдр
Инструкция по изготовлению трубогранника. Тетраэдр Теорема косинусов
Теорема косинусов Страна Математика
Страна Математика Интервальное оценивание параметров распределения случайных величин. Доверительный интервал
Интервальное оценивание параметров распределения случайных величин. Доверительный интервал Части задачи
Части задачи Числовые выражения
Числовые выражения Логарифмы и их свойства
Логарифмы и их свойства Презентация по математике "Пропорциональные величины" -
Презентация по математике "Пропорциональные величины" -  Всегда ли симметрично - это хорошо?
Всегда ли симметрично - это хорошо? График кусочно гладкой функции
График кусочно гладкой функции