Слайд 2Реши самостоятельно
В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать

из них двоих для участия в математической олимпиаде?
В магазине « Филателия» продается
8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Слайд 3Реши самостоятельно
Учащимся дали список из 10 книг, которые рекомендуется прочитать за лето.

Сколькими способами ученик может выбрать из них 6 книг?
Из лаборатории, в которой работают заведующая и 10 сотрудников, надо отправить 5 человек в командировку.Сколькими способами это можносделать, если а) заведующая должна ехать в командировку; б) заведующая должна остаться.
Слайд 4Задача №1
В классе учатся 16 мальчиков и 12 девочек. Для уборки территории

требуется выделить
4 мальчиков и 3 девочек. Сколькими способами это можно сделать?
Слайд 5Задача №2
Из 12 солдат , в число которых входят Иванов и Петров,

надо отправить в наряд трех человек. Сколькими способами это можно сделать, если:
а) Иванов и Петров должны пойти в наряд обязательно;
б) Иванов и Петров должны остаться; в) Иванов должен пойти в наряд, а Петров остаться.
Слайд 6Задача №3
Для ремонта школы прибыла бригада, состоящая из 12 человек. Трех из

них надо отправить на четвертый этаж, а четырех – на пятый. Сколькими способами это можно сделать?
Слайд 7Задача №4
В чемпионате России по футболу участвуют 16 команд. Перед началом чемпионата

газета « Спорт» провела Интернет - опрос читателей, задав два вопроса:1) какая команда получит золотые, какая – серебряные, какая – бронзовые награды; 2) какие две команды окажутся среди неудачников, т.е. займут два последних места? Читатели указали все возможные варианты.
Слайд 8а) Сколько вариантов состава неудачников указали участники опроса?
б) Сколько из них тех,

в которые входит команда « Динамо»?
в) сколько вариантов тройки призеров указали участники опроса?
г) сколько из них тех, в которые входят « Спартак» и « Зенит» ?







 08.09
08.09 Technologia informacyjna
Technologia informacyjna Первообразная функция
Первообразная функция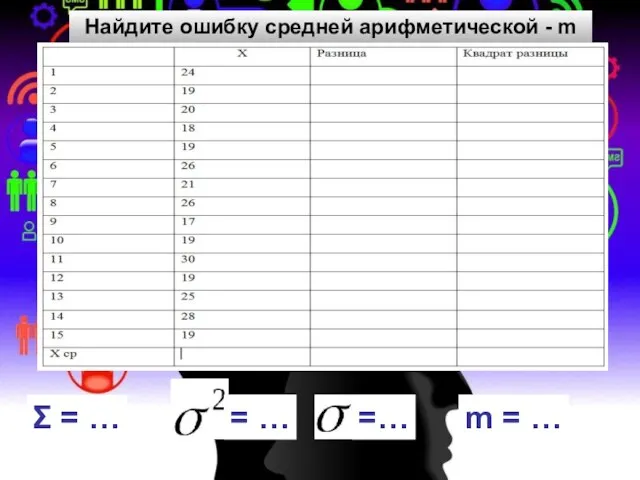 Средняя арифметическая
Средняя арифметическая Решение задач по теме Площадь параллелограмма, треугольника, трапеции
Решение задач по теме Площадь параллелограмма, треугольника, трапеции Логарифмические уравнения. Основные методы их решения
Логарифмические уравнения. Основные методы их решения Умножение. Законы умножения
Умножение. Законы умножения Определитель (детерминант) квадратной матрицы. Лекция 3
Определитель (детерминант) квадратной матрицы. Лекция 3 Числитель и знаменатель
Числитель и знаменатель Презентация на тему Счет от одного до десяти
Презентация на тему Счет от одного до десяти  Многогранники
Многогранники Критерий Стьюдента
Критерий Стьюдента Логарифм числа и его свойства
Логарифм числа и его свойства Непрерывные функции
Непрерывные функции Великолепная пятерка. Математический калейдоскоп
Великолепная пятерка. Математический калейдоскоп Умножение пяти, на 5 и соответствующие случаи деления. Математика 3 класс. Учителя начальных классов Лаишевской специальной школ
Умножение пяти, на 5 и соответствующие случаи деления. Математика 3 класс. Учителя начальных классов Лаишевской специальной школ Презентация на тему ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ
Презентация на тему ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ  Презентация на тему Основные тригонометрические формулы
Презентация на тему Основные тригонометрические формулы  Множества. Операции над множествами
Множества. Операции над множествами Координатный луч. Урок 2
Координатный луч. Урок 2 Математика. 2 класс. Задачи
Математика. 2 класс. Задачи Векторы (повторение). 8 класс
Векторы (повторение). 8 класс Частота и вероятность
Частота и вероятность Своя игра. Алгоритмы
Своя игра. Алгоритмы Тени основных геометрических фигур (по одной проекции)
Тени основных геометрических фигур (по одной проекции) Классы интегрируемых функций
Классы интегрируемых функций Презентация на тему Геометрические тела
Презентация на тему Геометрические тела  Решение задач по теме: Терема Пифагора
Решение задач по теме: Терема Пифагора