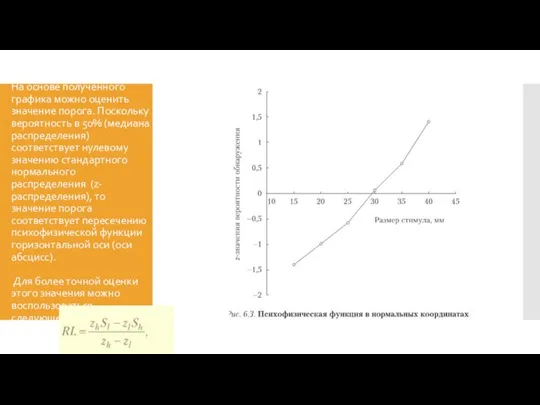
величиной стандартного отклонения, равного единице 1, необходимо проследить предполагаемые значения стимулов, которые будут соответствовать z -значениям, равным единице и минус единице.
Эти значения оказываются равными примерно 37,5 и 20 мм.
Более точно эти значения можно рассчитать формулам:
Sσ+ и Sσ- представляют собой искомые значения стимула, для которых результаты z -трансформации значений вероятности составляют соответственно 1 и –1.
Sh + и Sl + представляют собой имеющиеся в распоряжении значения стимулов, для которых величины z -трансформаций оказываются соответственно больше и меньше искомого единичного значения (для нашего примера эти величины стимулов оказываются равными 35 и 40 мм).
Соответствующие им значения z обозначены как zh+ и zl+ (для наших данных они оказываются равными 1,41 и 0,58). Подставляя эти значения в формулу, получаем значение 37,53 мм.



 Состав чисел первого десятка
Состав чисел первого десятка Отрезок. Сравнение отрезков
Отрезок. Сравнение отрезков Занимательная математика
Занимательная математика Переменная величина
Переменная величина Интересное о математике
Интересное о математике Понятие логарифма
Понятие логарифма Устный счёт. Закрепление изученного
Устный счёт. Закрепление изученного Определители
Определители Таблица умножения трёх
Таблица умножения трёх Множество. Элемент множества
Множество. Элемент множества Логические схемы
Логические схемы Игры. Памятка
Игры. Памятка Двугранный угол. Перпендикулярность плоскостей
Двугранный угол. Перпендикулярность плоскостей Цилиндр. Конус
Цилиндр. Конус Випадкова подія. Відносна частота події. Імовірність події
Випадкова подія. Відносна частота події. Імовірність події Решение тригонометрических уравнений
Решение тригонометрических уравнений Презентация по математике "Логарифмическая функция. Преобразования графиков." -
Презентация по математике "Логарифмическая функция. Преобразования графиков." -  Интервальные оценки
Интервальные оценки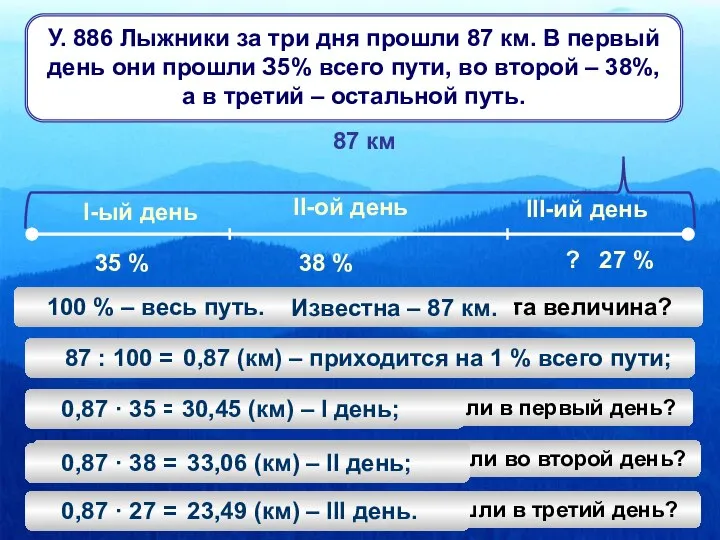 Задачи о лыжниках
Задачи о лыжниках Окружность. Проверочная работа
Окружность. Проверочная работа ГИА - 2016. Задачи №9,10,11,12
ГИА - 2016. Задачи №9,10,11,12 Решение уравнений и неравенств. Линейные уравнения и неравенства
Решение уравнений и неравенств. Линейные уравнения и неравенства Уравнение окружности
Уравнение окружности Тригонометрические уравнения
Тригонометрические уравнения Решение задач с помощью чертежа
Решение задач с помощью чертежа Арифметические действия с дробями
Арифметические действия с дробями Вписанная окружность
Вписанная окружность Задачи на концентрацию, сплавы. Подготовка к ЕГЭ
Задачи на концентрацию, сплавы. Подготовка к ЕГЭ