Содержание
- 2. Определение: Случайной называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств. Например: число
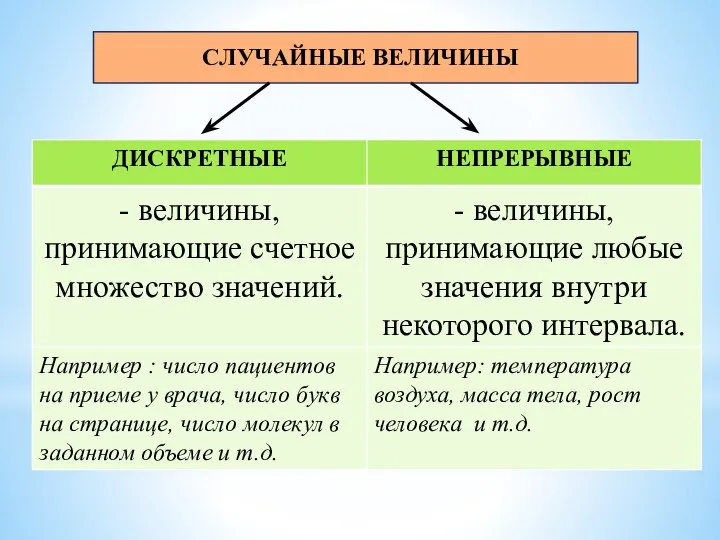
- 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
- 4. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Законом распределения случайной величины называется совокупность всех возможных значений этой величины и, соответствующих
- 5. Закон распределения может быть представлен также в виде формулы или графика (т.е. графически). Основные особенности закона
- 6. В законе распределения могут быть один, два и более максимумов вероятности. Каждое значение случайной величины, соответствующее
- 7. ЗАДАЧИ 1. При исследовании скорости распространения механической волны на поражённых участках кожи у больных псориазом в
- 8. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 1. Число девушек в двадцати учебных группах равно соответственно 8, 5, 7,
- 9. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ В случае непрерывной случайной величины нельзя написать закон распределения в виде таблицы, поскольку
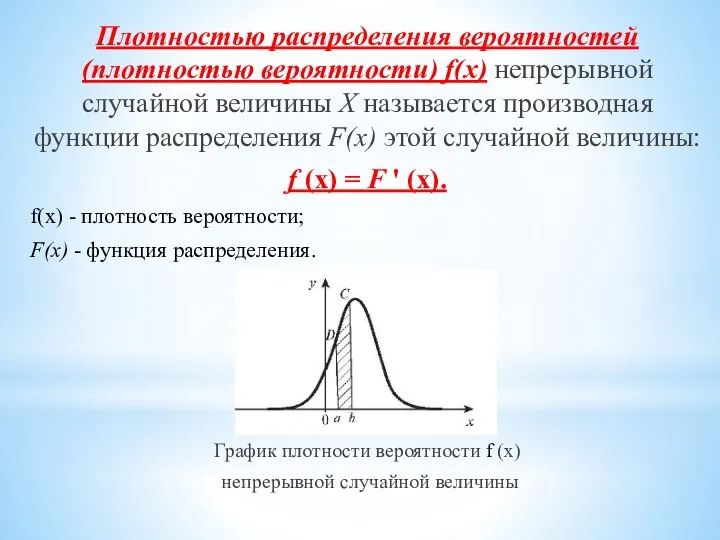
- 10. Плотностью распределения вероятностей (плотностью вероятности) f(x) непрерывной случайной величины X называется производная функции распределения F(x) этой
- 11. Плотность вероятности (функция распределения) показывает, как меняется вероятность, отнесенная к интервалу dx случайной величины, в зависимости
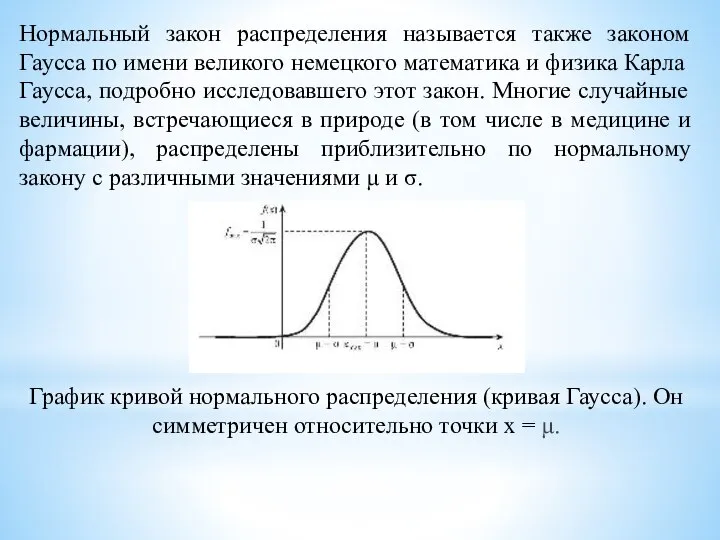
- 12. Нормальный закон распределения называется также законом Гаусса по имени великого немецкого математика и физика Карла Гаусса,
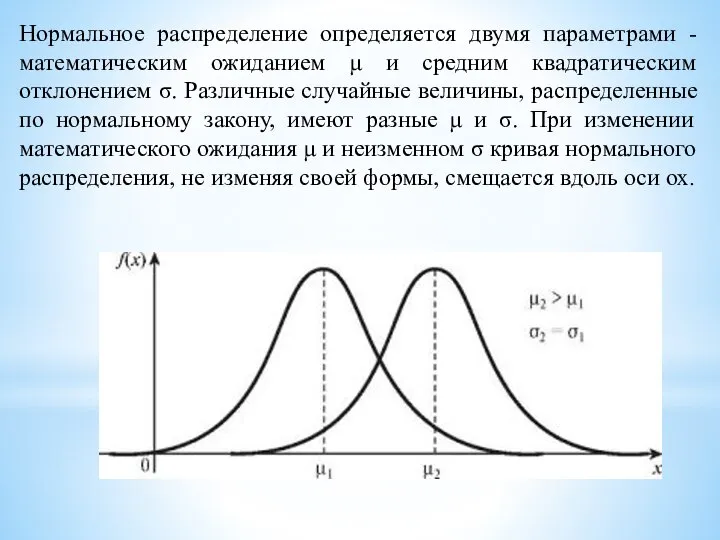
- 13. Нормальное распределение определяется двумя параметрами - математическим ожиданием μ и средним квадратическим отклонением σ. Различные случайные
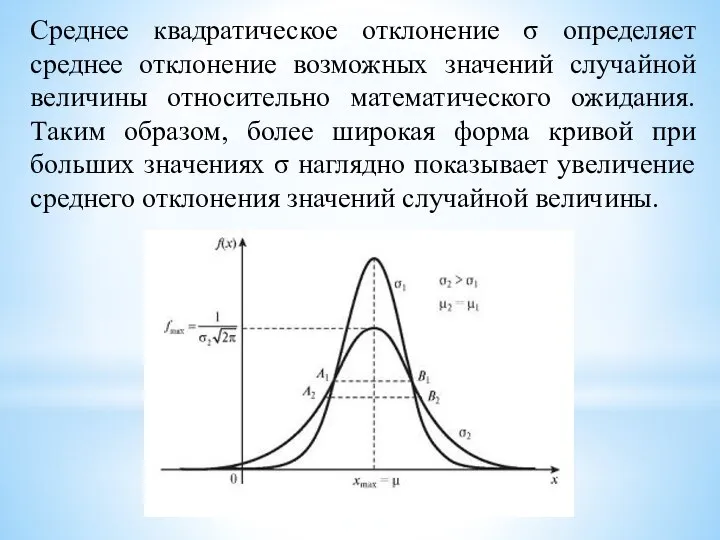
- 14. Среднее квадратическое отклонение σ определяет среднее отклонение возможных значений случайной величины относительно математического ожидания. Таким образом,
- 16. Скачать презентацию








 Преобразование иррациональных выражений
Преобразование иррациональных выражений задачи
задачи Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Полное исследование функций и построение их графиков
Полное исследование функций и построение их графиков Занимательные задачи
Занимательные задачи Презентация на тему Отношения и пропорции
Презентация на тему Отношения и пропорции  Поле чудес. Геометрия 9 класс
Поле чудес. Геометрия 9 класс Решение задач по теме: Терема Пифагора
Решение задач по теме: Терема Пифагора КОМПЛЕКСНЫЕ ЧИСЛА
КОМПЛЕКСНЫЕ ЧИСЛА Результант. Литература
Результант. Литература Метод экспоненциального сглаживания
Метод экспоненциального сглаживания Равнобедренный треугольник и его свойства
Равнобедренный треугольник и его свойства Старинные меры массы и длины
Старинные меры массы и длины Математические ребусы
Математические ребусы Решение задач на движение
Решение задач на движение ЭГЕ по математике. Прототип 18. Задачи с параметром. Применение свойств функции
ЭГЕ по математике. Прототип 18. Задачи с параметром. Применение свойств функции Зачем строят корабли? (окружающий мир). 1 класс
Зачем строят корабли? (окружающий мир). 1 класс Решение систем уравнений с двумя переменными методом подстановки
Решение систем уравнений с двумя переменными методом подстановки Математическая карусель
Математическая карусель Решение систем уравнений способом подстановки
Решение систем уравнений способом подстановки Презентация на тему Задачи по теме "Обыкновенные дроби"
Презентация на тему Задачи по теме "Обыкновенные дроби" 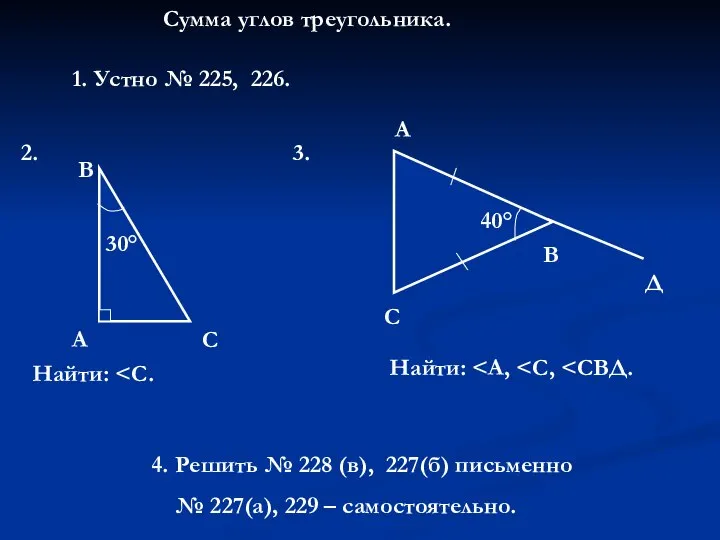 Сумма углов треугольника
Сумма углов треугольника Правильные многогранники в природе
Правильные многогранники в природе Теорема синусов и косинусов
Теорема синусов и косинусов Квадартные уравнения. Основные понятия
Квадартные уравнения. Основные понятия Использование деревьев при решении алгоритмических задач
Использование деревьев при решении алгоритмических задач Умножение обыкновенных дробей
Умножение обыкновенных дробей Многоугольники в жизни
Многоугольники в жизни