Содержание
- 2. 0. Введение. Общие сведения. Объем курса – 18 часов лекции 16 часов лабораторные занятия Лабораторные занятия
- 3. 0. Введение. Что такое компьютерный анализ данных Компьютерный анализ данных - научное направление, объединяющее вероятностно-статистические, логико-алгебраические,
- 4. 0. Введение. Основные разделы Статистический анализ данных (Statistical Data Analysis – SDA) Интеллектуальный анализ данных (Data
- 5. 0. Введение. Литература. Ширяев А.Н. Вероятность. Москва, 1980. Вентцель Е.С. Теория вероятностей: Учеб. для вузов. —
- 6. 1. Основные понятия теории вероятностей Теория вероятностей - математическая наука, изучающая закономерности в случайных явлениях Случайное
- 7. 1. Основные понятия теории вероятностей Примеры случайных явлений Стрельба из орудия, установленного под заданным углом к
- 8. 1. Основные понятия теории вероятностей Примеры случайных явлений Взвешивание одного и того же тела на аналитических
- 9. 1. Основные понятия теории вероятностей Примеры случайных явлений Бросание игральной кости Детерминированы: форма (куб) и распределение
- 10. 1. Основные понятия теории вероятностей Какие закономерности изучает теория вероятностей Теория вероятностей изучает закономерности, проявляющиеся при
- 11. 1. Основные понятия теории вероятностей Событие Под «событием» в теории вероятностей понимается всякий факт, который в
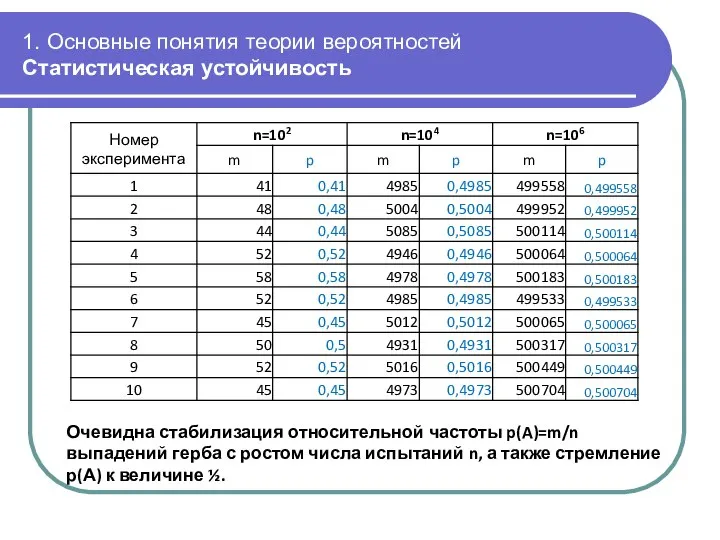
- 12. 1. Основные понятия теории вероятностей Статистическая устойчивость Если А – некоторое случайное событие, то доля m/n
- 13. 1. Основные понятия теории вероятностей Статистическая устойчивость Очевидна стабилизация относительной частоты p(A)=m/n выпадений герба с ростом
- 14. 1. Основные понятия теории вероятностей. Пространство элементарных исходов. Пространством элементарных событий Ω называется множество, содержащее все
- 15. 1. Основные понятия теории вероятностей. Пространство элементарных исходов. Пример: однократное подбрасывание игральной кости. Пространством элементарных событий
- 16. 1. Основные понятия теории вероятностей. Вероятность на дискретном пространстве элементарных исходов
- 17. 1. Основные понятия теории вероятностей. Свойства вероятности на дискретном пространстве элементарных исходов
- 18. 1. Основные понятия теории вероятностей. Классическое определение вероятности
- 19. 1. Основные понятия теории вероятностей. Классическое определение вероятности
- 20. 1. Основные понятия теории вероятностей. Вероятность и частота
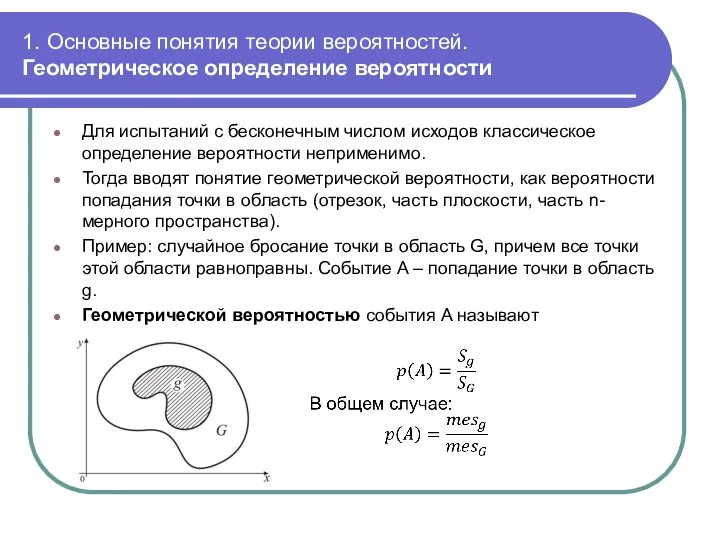
- 21. 1. Основные понятия теории вероятностей. Геометрическое определение вероятности Для испытаний с бесконечным числом исходов классическое определение
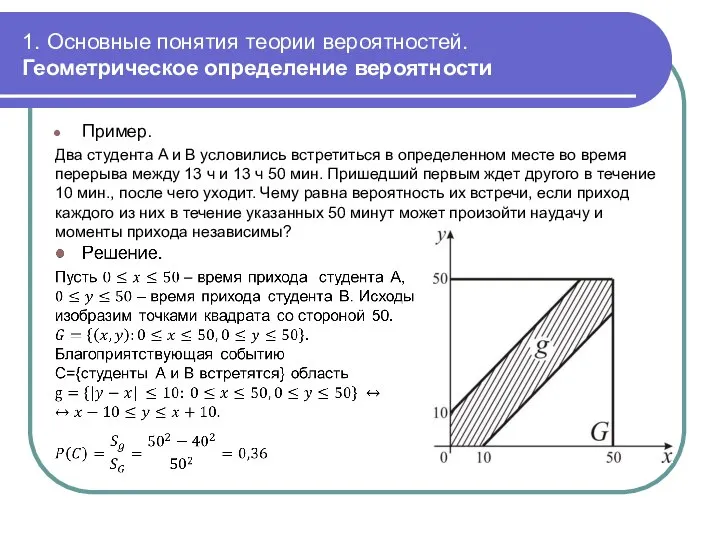
- 22. 1. Основные понятия теории вероятностей. Геометрическое определение вероятности Пример. Два студента A и B условились встретиться
- 23. 1. Основные понятия теории вероятностей. Условная вероятность Пример. Игральная кость подбрасывается один раз. Известно, что выпало
- 24. 1. Основные понятия теории вероятностей. Правило умножения вероятностей событий Правило умножения вероятностей: Вероятность произведения двух событий
- 25. 1. Основные понятия теории вероятностей. Формула полной вероятности
- 26. 1. Основные понятия теории вероятностей. Формула полной вероятности Пример. Имеется четыре одинаковых ящика с электрическими лампочками,
- 27. 1. Основные понятия теории вероятностей. Формула Байеса
- 28. 2. Случайные величины и их характеристики Понятие случайной величины Случайной величиной называется величина которая в результате
- 29. 2. Случайные величины и их характеристики Закон распределения Законом распределения случайной величины называется всякое соотношение, устанавливающее
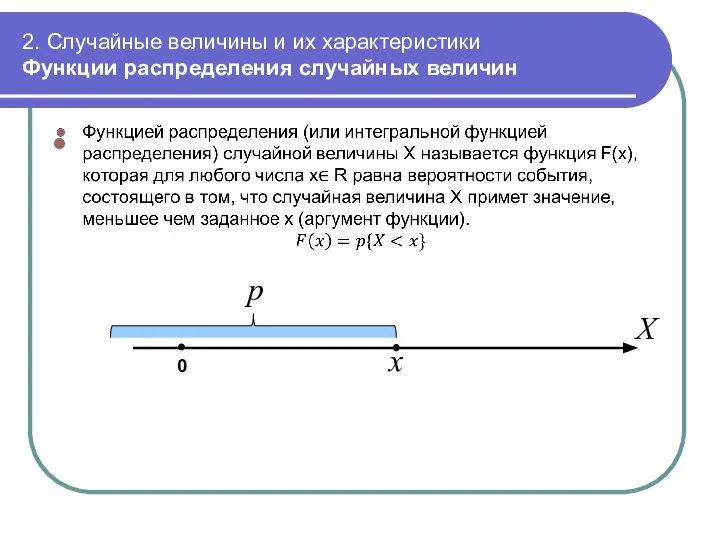
- 30. 2. Случайные величины и их характеристики Функции распределения случайных величин 0 x X p
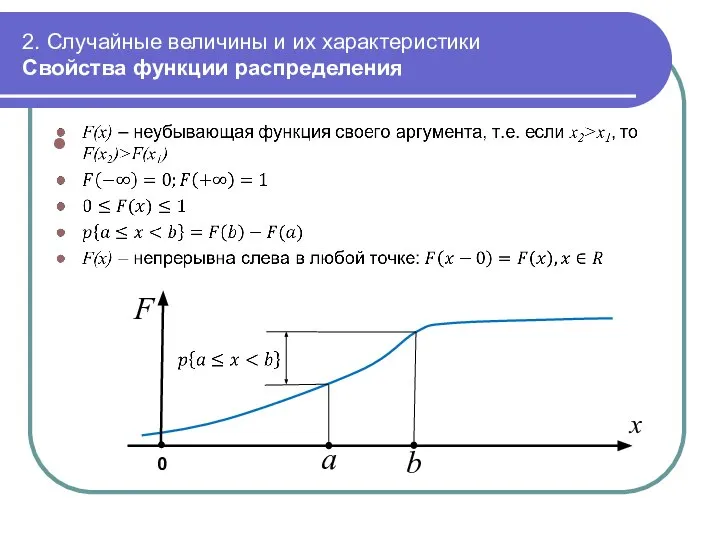
- 31. 2. Случайные величины и их характеристики Свойства функции распределения 0 a x b F
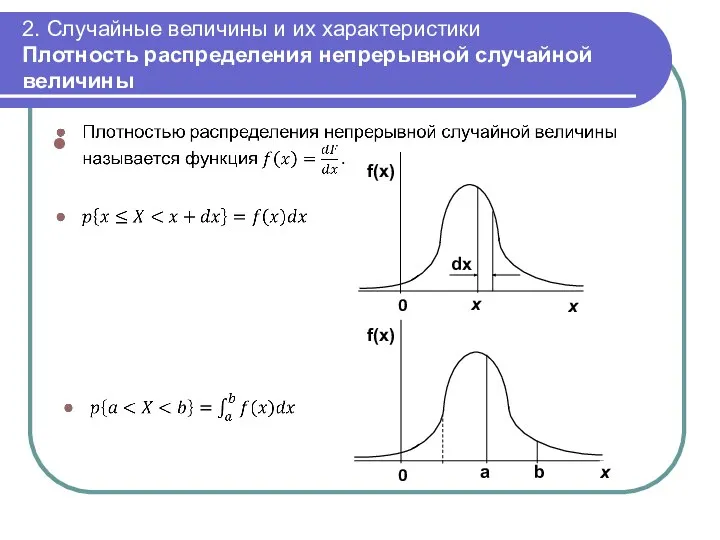
- 32. 2. Случайные величины и их характеристики Плотность распределения непрерывной случайной величины dx f(x) f(x) a b
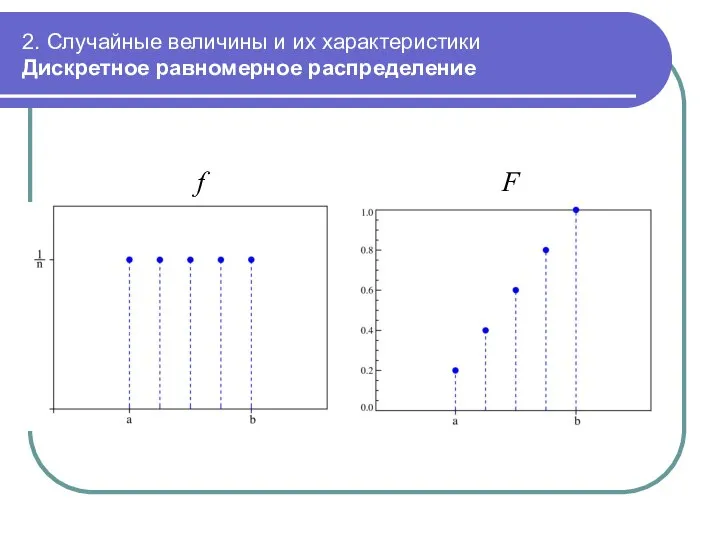
- 33. 2. Случайные величины и их характеристики Дискретное равномерное распределение f F
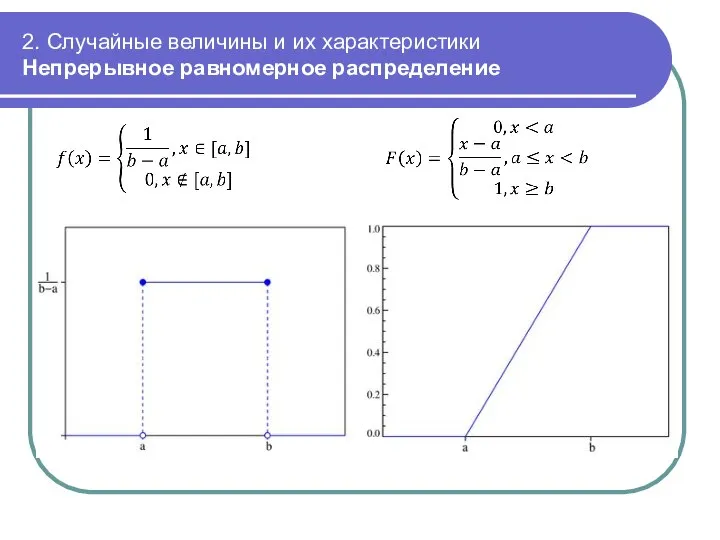
- 34. 2. Случайные величины и их характеристики Непрерывное равномерное распределение
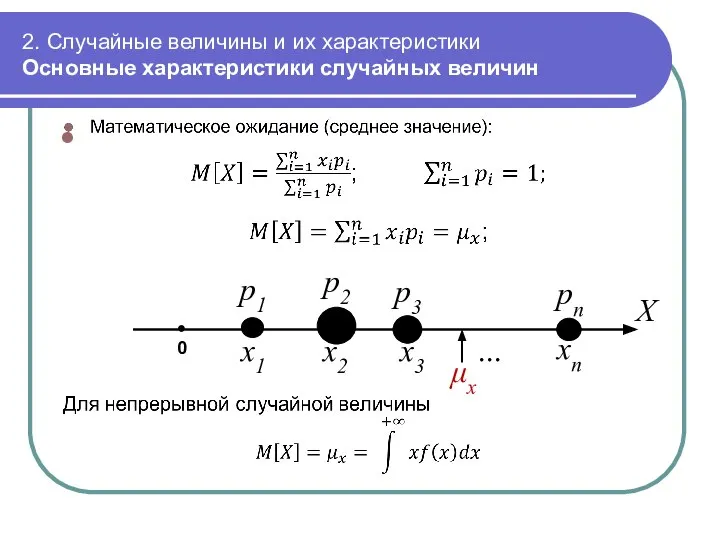
- 35. 2. Случайные величины и их характеристики Основные характеристики случайных величин 0 x1 X p1 x2 x3
- 36. 2. Случайные величины и их характеристики Основные характеристики случайных величин
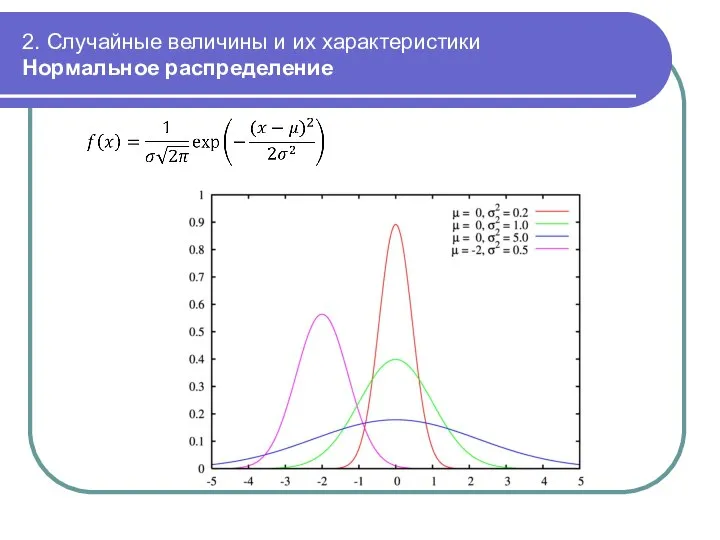
- 37. 2. Случайные величины и их характеристики Нормальное распределение
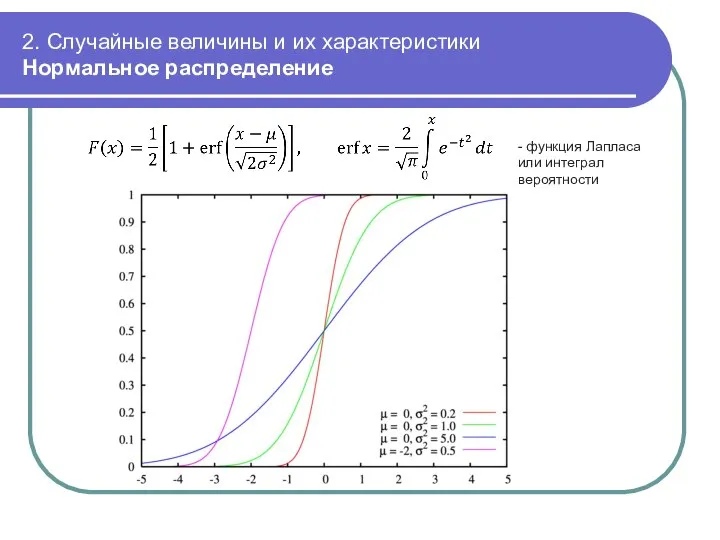
- 38. 2. Случайные величины и их характеристики Нормальное распределение - функция Лапласа или интеграл вероятности
- 39. 2. Случайные величины и их характеристики Понятие случайного процесса 0 t t1 t2
- 40. 2. Случайные величины и их характеристики Основные задачи статистики Предмет математической статистики – разработка методов регистрации,
- 41. 2. Случайные величины и их характеристики Генерация псевдослучайных последовательностей Источники настоящих последовательностей случайных чисел – случайные
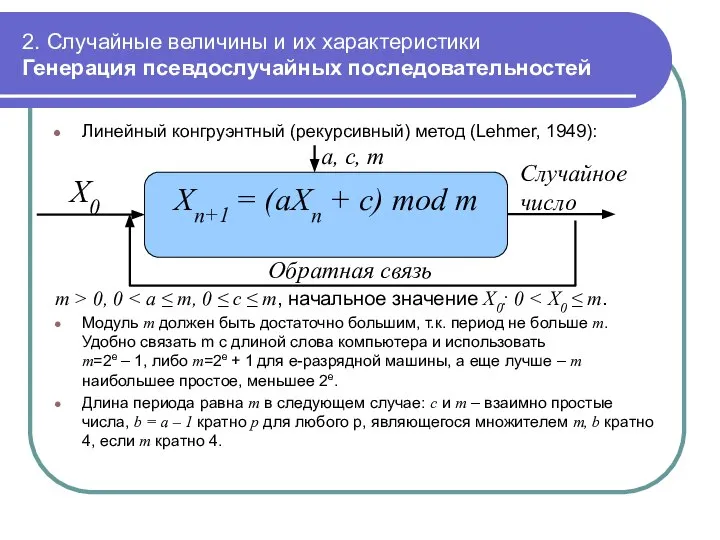
- 42. 2. Случайные величины и их характеристики Генерация псевдослучайных последовательностей Линейный конгруэнтный (рекурсивный) метод (Lehmer, 1949): m
- 43. 2. Случайные величины и их характеристики Генерация псевдослучайных последовательностей Генератор MS FORTRAN: m = 231-1, c=0,
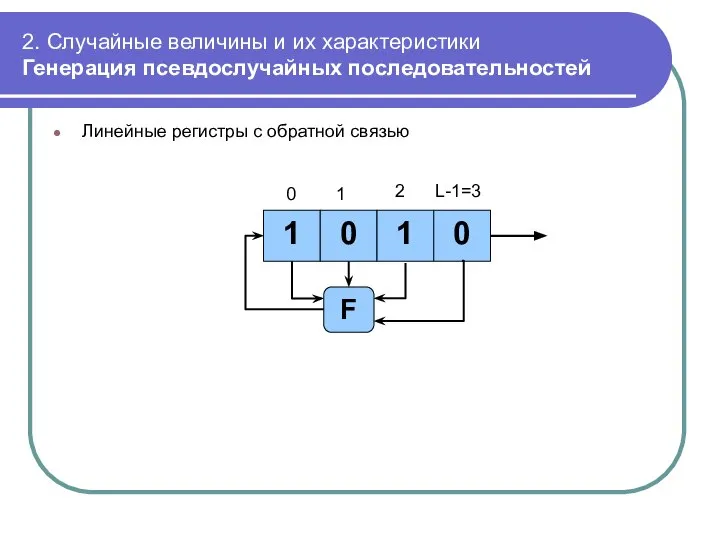
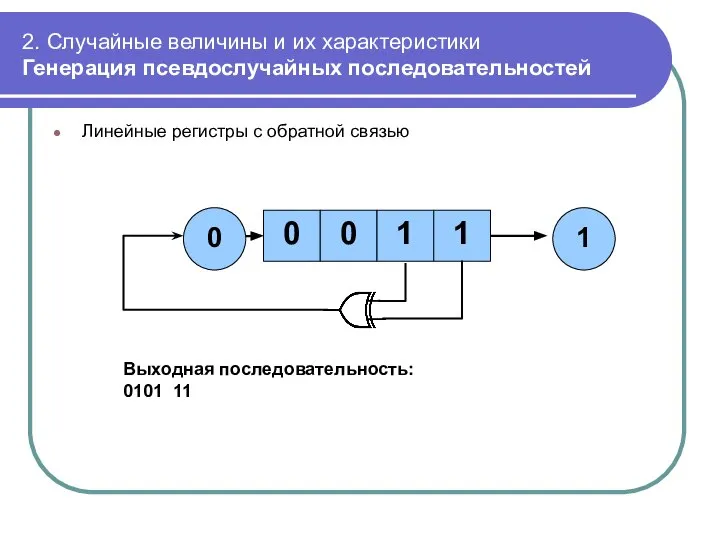
- 44. 2. Случайные величины и их характеристики Генерация псевдослучайных последовательностей Линейные регистры с обратной связью 1 0
- 45. 2. Случайные величины и их характеристики Генерация псевдослучайных последовательностей 1 0 1 0 0 1 2
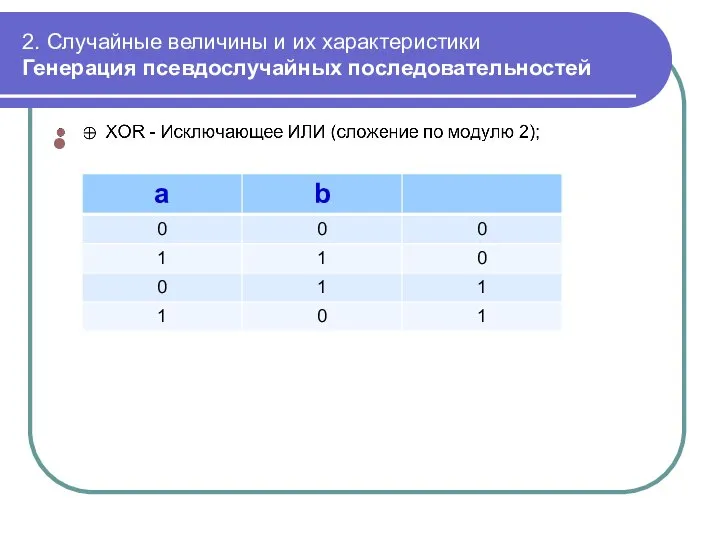
- 46. 2. Случайные величины и их характеристики Генерация псевдослучайных последовательностей
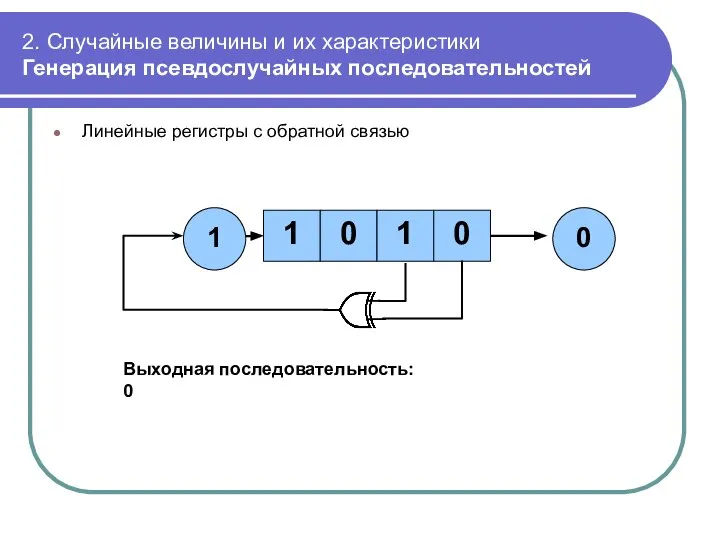
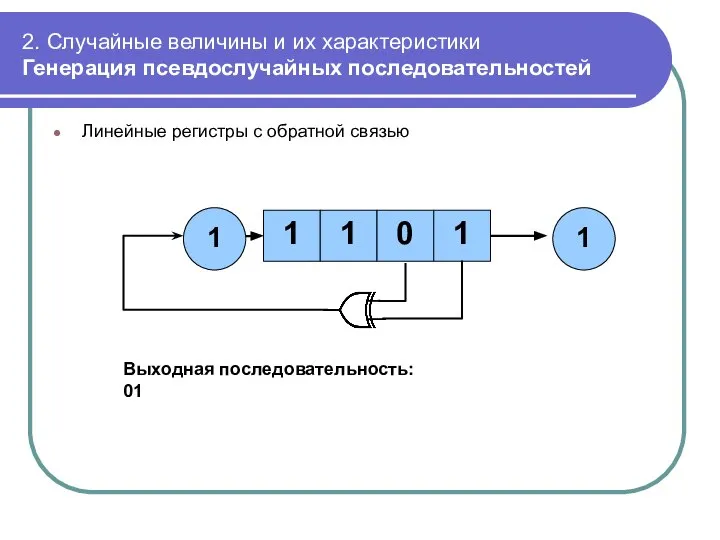
- 47. 2. Случайные величины и их характеристики Генерация псевдослучайных последовательностей Линейные регистры с обратной связью 1 0
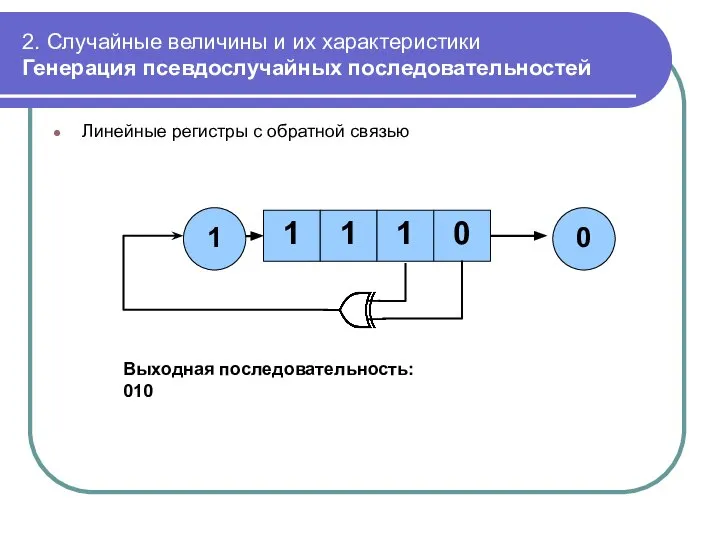
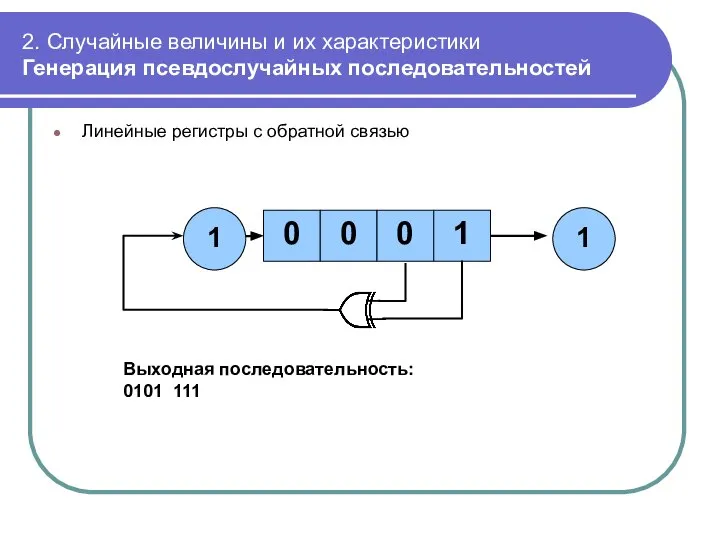
- 48. 2. Случайные величины и их характеристики Генерация псевдослучайных последовательностей Линейные регистры с обратной связью 1 1
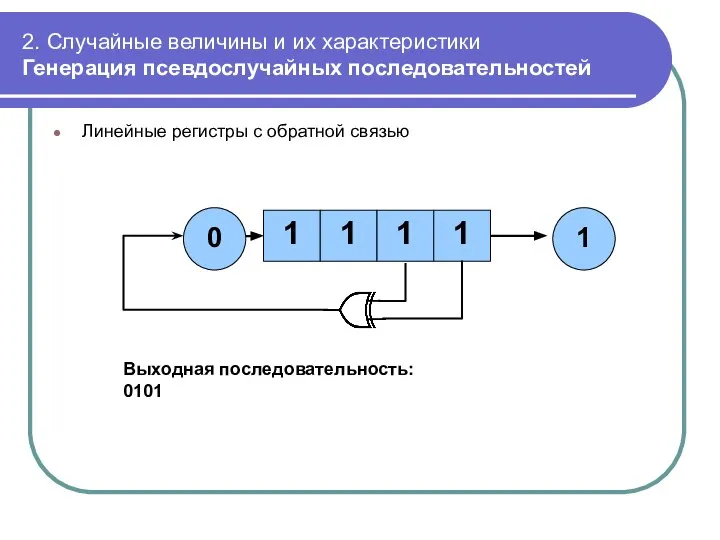
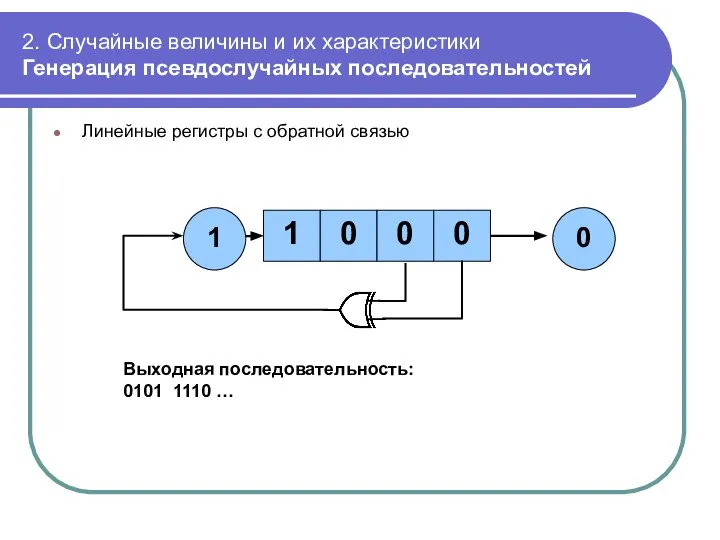
- 49. 2. Случайные величины и их характеристики Генерация псевдослучайных последовательностей Линейные регистры с обратной связью 1 1
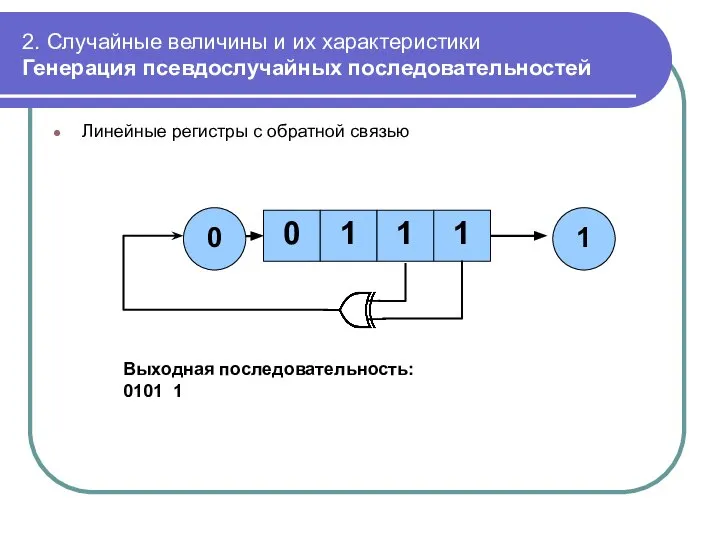
- 50. 2. Случайные величины и их характеристики Генерация псевдослучайных последовательностей Линейные регистры с обратной связью 1 1
- 51. 2. Случайные величины и их характеристики Генерация псевдослучайных последовательностей Линейные регистры с обратной связью 0 1
- 52. 2. Случайные величины и их характеристики Генерация псевдослучайных последовательностей Линейные регистры с обратной связью 0 0
- 53. 2. Случайные величины и их характеристики Генерация псевдослучайных последовательностей Линейные регистры с обратной связью 0 0
- 54. 2. Случайные величины и их характеристики Генерация псевдослучайных последовательностей Линейные регистры с обратной связью 1 0
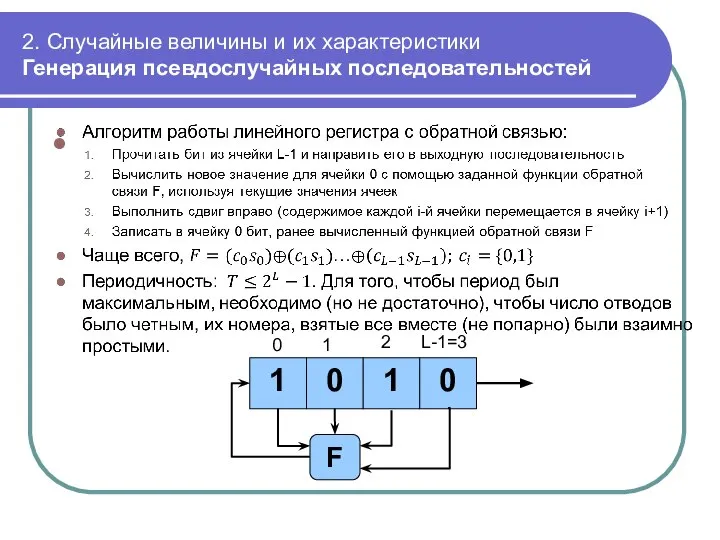
- 55. 2. Случайные величины и их характеристики Генерация псевдослучайных последовательностей Недостатки генераторов псевдослучайных чисел: Конечный период Последовательные
- 56. 2. Случайные величины и их характеристики Генерация псевдослучайных последовательностей Основные критерии криптостойкости: Нет аналитической зависимости между
- 58. Скачать презентацию
































 Математическая статистика. Лекция 2
Математическая статистика. Лекция 2 Разработка обучающей программы по нахождению элементов треугольника
Разработка обучающей программы по нахождению элементов треугольника Циліндр. Елементи циліндра
Циліндр. Елементи циліндра Ряды Фурье. Лекция 3.10
Ряды Фурье. Лекция 3.10 Числовые последовательности
Числовые последовательности Игра-тренажер А знаете ли вы…. Математика 3 класс
Игра-тренажер А знаете ли вы…. Математика 3 класс Статистические гипотезы и их проверка
Статистические гипотезы и их проверка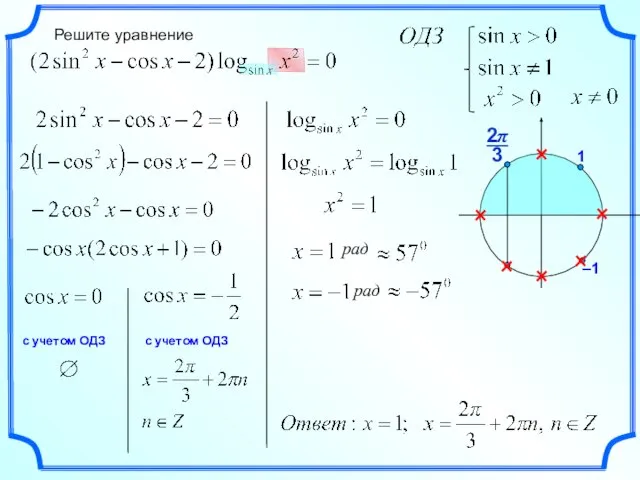 Решение уравнения
Решение уравнения Задачи на подсчет числа размещений, перестановок, сочетаний
Задачи на подсчет числа размещений, перестановок, сочетаний Способы задания зависимостей между величинами: аналитический, табличный, графический
Способы задания зависимостей между величинами: аналитический, табличный, графический Уравнения и неравенства с параметрами. 11 класс
Уравнения и неравенства с параметрами. 11 класс Все действия с дробями
Все действия с дробями Презентация на тему Сфера
Презентация на тему Сфера  Метод экспоненциального сглаживания
Метод экспоненциального сглаживания Основные положения теории групп
Основные положения теории групп Десятичные дроби
Десятичные дроби Презентация на тему Производная функции
Презентация на тему Производная функции  pril1
pril1 Лекция. Дифференциальные уравнения
Лекция. Дифференциальные уравнения Логика - это русло мысли
Логика - это русло мысли Система пропорционирования в проектировании объектов дизайна
Система пропорционирования в проектировании объектов дизайна Комбинированные уравнения. Задания для устного счета
Комбинированные уравнения. Задания для устного счета Числовые ряды
Числовые ряды Коэффициенты линейной функции
Коэффициенты линейной функции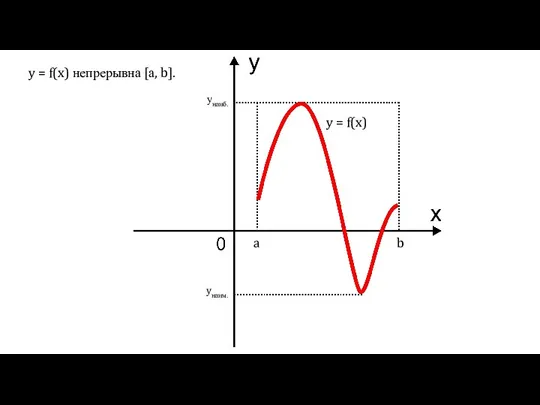 Применение производной
Применение производной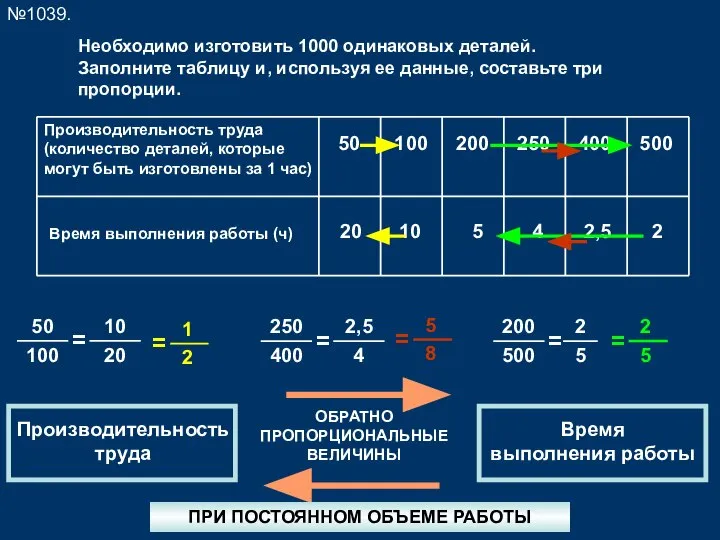 Пропорциональные величины
Пропорциональные величины Задачи с величинами цена, количество, стоимость
Задачи с величинами цена, количество, стоимость Проценты. 6 класс
Проценты. 6 класс