Содержание
- 2. Цели урока дать определение высоты параллелограмма ; доказать теорему о площади параллелограмма; показать применение формулы в
- 3. План урока 1. Организационный момент 2. Устные упражнения, тест на повторение 3. Задача 4. Объяснение нового
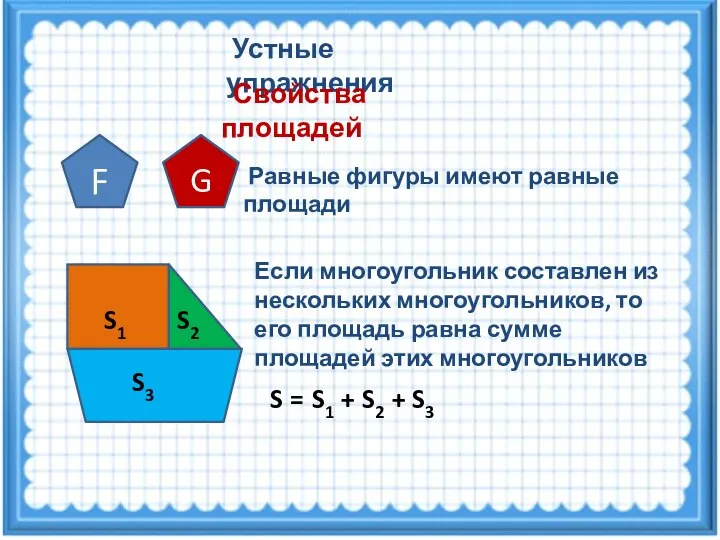
- 4. Устные упражнения Свойства площадей F G Равные фигуры имеют равные площади S1 S2 S3 Если многоугольник
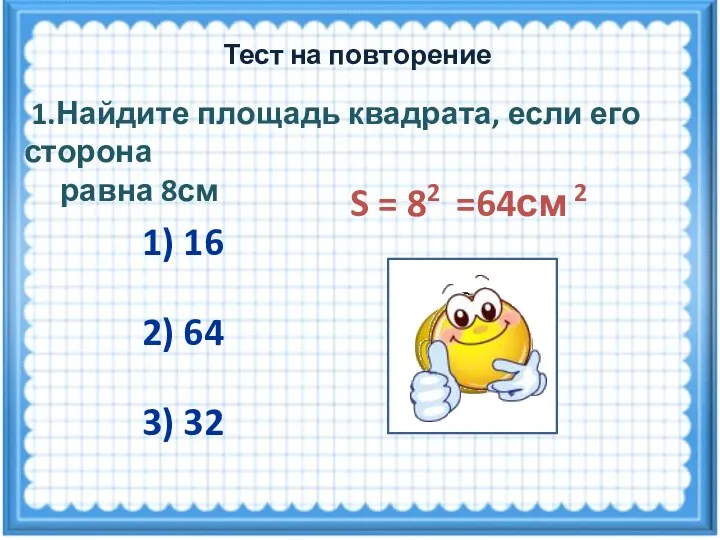
- 5. S = 82 =64см 2 1.Найдите площадь квадрата, если его сторона равна 8см 1) 16 2)
- 6. а = 4см Р = 4·4 =16см 2.Найдите периметр квадрата, если площадь равна 16 см2 1)
- 7. S =10 2:2=50см2 3.Найдите площадь треугольника, если его катеты равны по 10см 3) 20 1) 50
- 8. S = 10·8 = 80см2 4.Найдите площадь прямоугольника, если его смежные стороны равны 10см и 8см
- 9. S = (4·8):2= 16см2 2) 32 3) 16 1) 24 Тест на повторение 4 8 5.Найдите
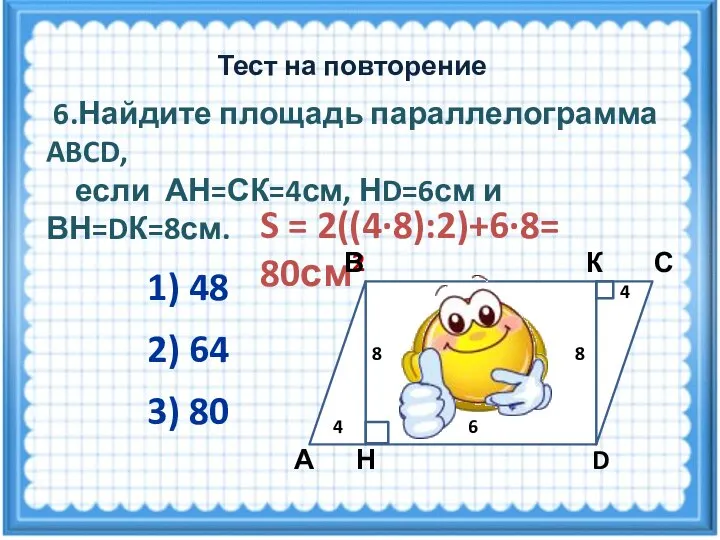
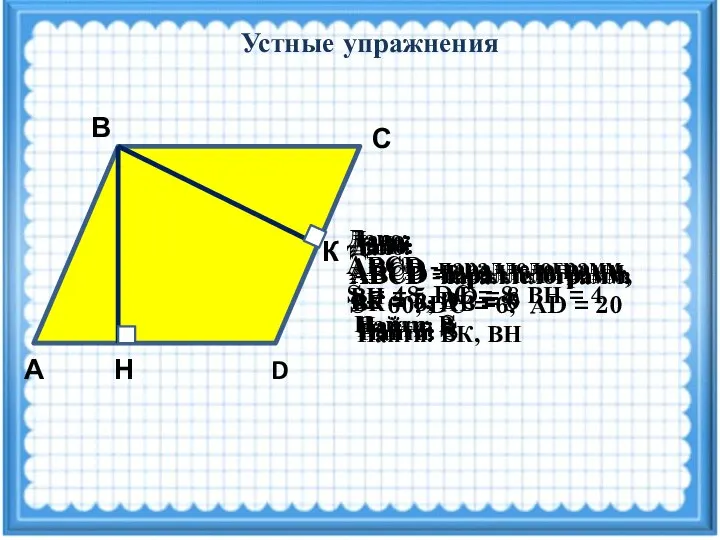
- 10. S = 2((4·8):2)+6·8= 80см2 6.Найдите площадь параллелограмма ABCD, если АН=СК=4см, НD=6см и ВН=DК=8см. 2) 64 3)
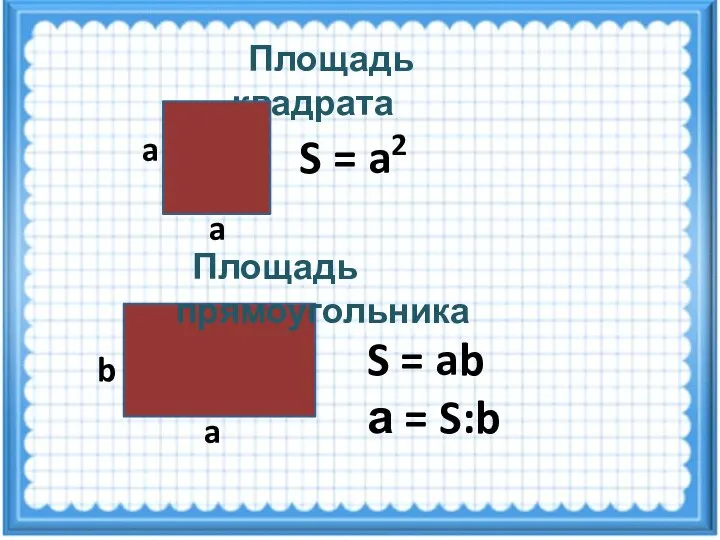
- 11. Площадь квадрата S = a2 a a b a S = ab а = S:b Площадь
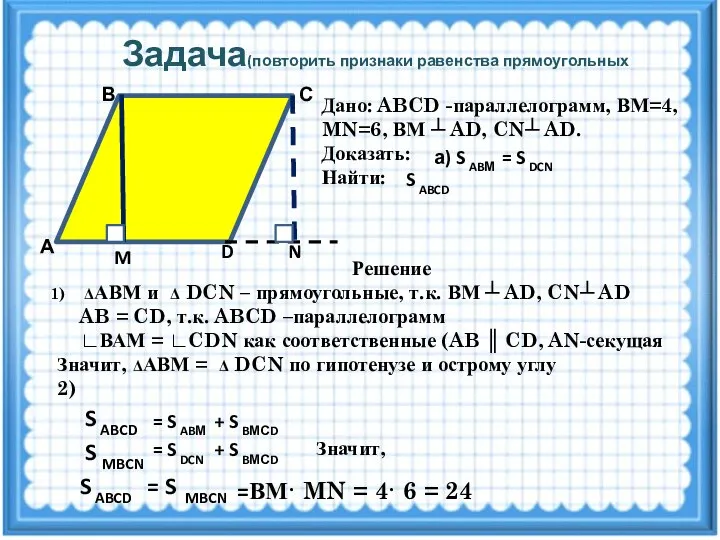
- 12. Задача(повторить признаки равенства прямоугольных треугольников) А D M N С В Дано: ABCD -параллелограмм, ВМ=4, MN=6,
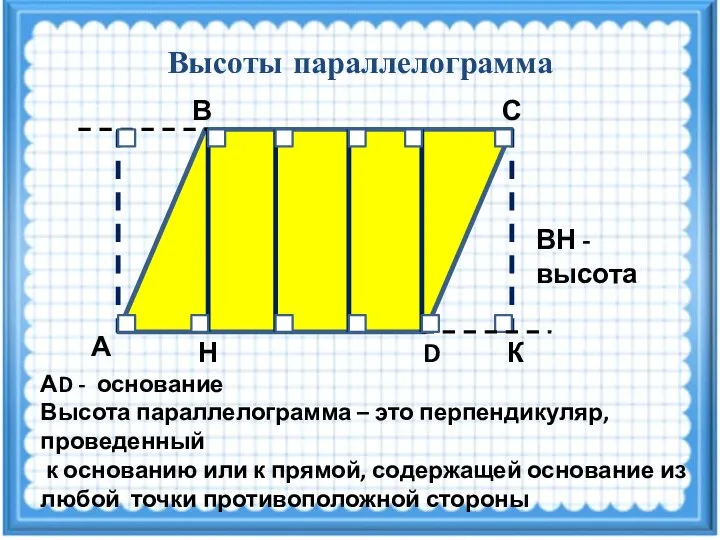
- 13. Высоты параллелограмма С В А D Н К ВН - высота АD - основание Высота параллелограмма
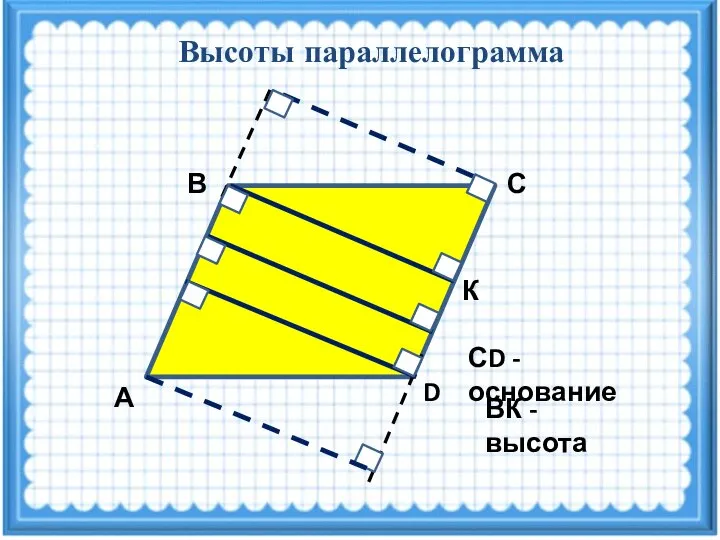
- 14. Высоты параллелограмма С В А D К СD - основание ВК - высота
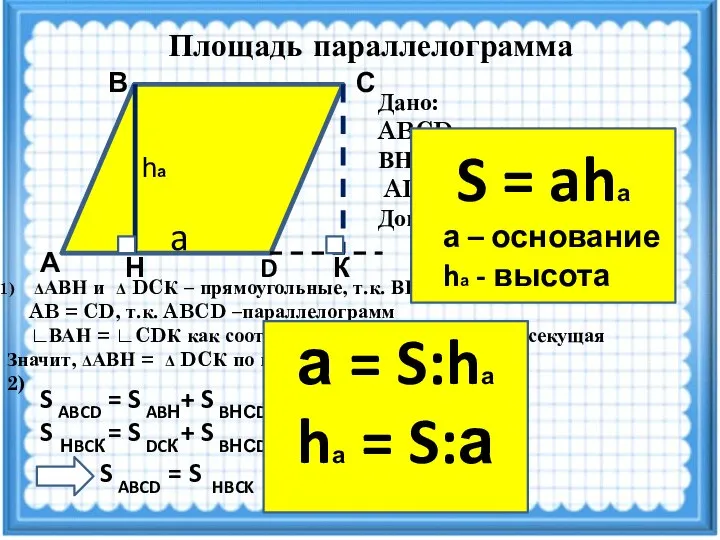
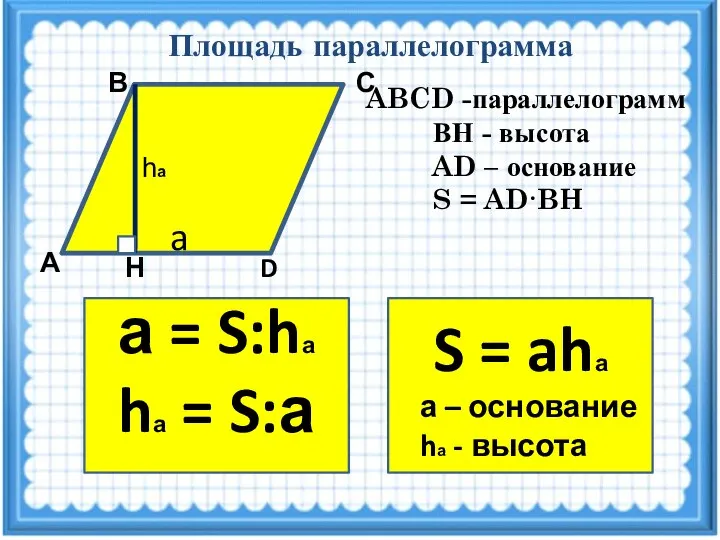
- 15. Площадь параллелограмма Т Площадь параллелограмма равна произведению его основания на высоту.
- 16. Площадь параллелограмма А D Н К С В Дано: ABCD -параллелограмм, ВН - высота AD -
- 17. Устные упражнения А D Н С В Дано: ABCD -параллелограмм, ВК = 5, DC = 6
- 18. Закрепление изученного материала №461
- 19. Площадь параллелограмма А D Н С В ABCD -параллелограмм ВН - высота AD – основание S
- 20. Домашнее задание п. 51, №460, №462.
- 22. Скачать презентацию









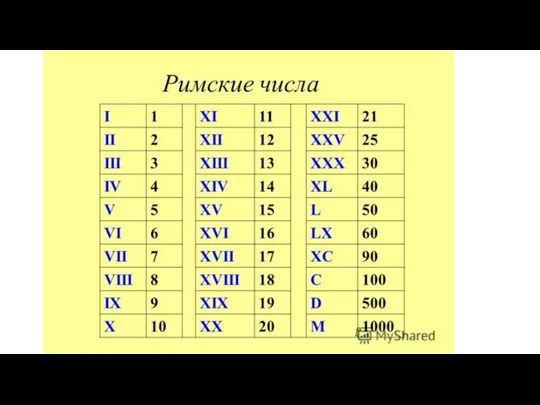 Римские числа
Римские числа Прямоугольный треугольник
Прямоугольный треугольник Уравнение плоскости
Уравнение плоскости Движение. Осевая симметрия
Движение. Осевая симметрия Таблицы умножения и деления на 2 и 3
Таблицы умножения и деления на 2 и 3 Распределительный закон
Распределительный закон Показательные неравенства
Показательные неравенства Презентация на тему Комбинаторика
Презентация на тему Комбинаторика  Презентация на тему Понятие угла
Презентация на тему Понятие угла  Подсчитай, сколько
Подсчитай, сколько Красная Шапочка. Интерактивная игра по математике
Красная Шапочка. Интерактивная игра по математике Усвоение соответствий понятий о свойствах функции и её производной. Открытый банк заданий ЕГЭ
Усвоение соответствий понятий о свойствах функции и её производной. Открытый банк заданий ЕГЭ Ãkom Erikom do 100
Ãkom Erikom do 100 Линейная алгебра. Лекция №2. Часть 2
Линейная алгебра. Лекция №2. Часть 2 Проценты. Сравнение с целым
Проценты. Сравнение с целым График функции
График функции Своя игра по математике
Своя игра по математике Презентация на тему Наука и образование в Древней Греции
Презентация на тему Наука и образование в Древней Греции  54 задачи на чертежах по планиметрии. Теорема Пифагора
54 задачи на чертежах по планиметрии. Теорема Пифагора Своя игра (2)
Своя игра (2) Открытия науки в России 10-12 в
Открытия науки в России 10-12 в Вероятность в карточных играх
Вероятность в карточных играх Начала стереометрии
Начала стереометрии Упрощение выражений. Решение уравнений
Упрощение выражений. Решение уравнений Прямоугольный треугольник и его свойства
Прямоугольный треугольник и его свойства Многочлен и его стандартный вид
Многочлен и его стандартный вид Алгебра. Число. Уравнение. Тождество. Функция
Алгебра. Число. Уравнение. Тождество. Функция Движение по окружности. Подборка задач
Движение по окружности. Подборка задач