Рівняння дотичної до графіка функції

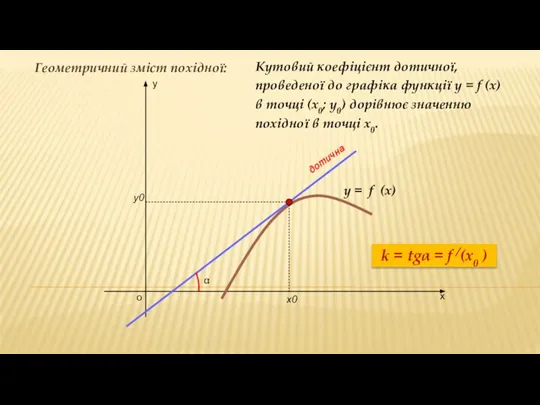
ГЕОМЕТРИЧНИЙ ЗМІСТ ПОХІДНОЇ:
Кутовий коефіцієнт дотичної,
проведеної до графіка функції у = f (x)
в точці з абсцисою х0 дорівнює значенню
похідної функції в цій точці.
α – кут нахилу дотичної до додатного напряму осі Ох
k = f /(x0 ) = tgα

х
у
о
y = f (x)
х0
у0
Геометричний зміст похідної:
α
Кутовий коефіцієнт дотичної,
проведеної до графіка функції у = f (x)
в точці (х0; у0) дорівнює значенню
похідної в точці х0.
k = tgα = f /(x0 )
дотична

РІВНЯННЯ ДОТИЧНОЇ ДО ГРАФІКА ФУНКЦІЇ

АЛГОРИТМ СКЛАДАННЯ РІВНЯННЯ ДОТИЧНОЇ
ДО ГРАФІКА ФУНКЦІЇ
Нехай ƒ (х) – дана функція,
x0 – дана точка, що належить графіку функції
1. Знайти значення функції в точці x0
2. Знайти похідну функції f /(x )
3. Знайти значення похідної функції в точці x0 f /(x0 )
4. Записати рівняння дотичної, підставивши знайдені
в пункті 1 та пункті 3 значення в рівняння дотичної

Розв’язання:
1. Знайдемо значення функції в точці x0 = -2 : f(x0) = f(-2) = 2 · (-2)2+5 · (-2) = 8 - 10 = -2
2. Знайдемо похідну функції f‘(x ) : fʹ(x) = (2х2+5х)ʹ = 4х + 5
3. Знайдемо значення похідної функції в точці x0 = -2 : f‘(x0 ) = fʹ(-2) = 4 · (-2) + 5 = -8 + 5 = -3
Зверніть увагу f‘(x0 ) ≠ f(x0)
4. Запишемо рівняння дотичної, підставивши знайдені в пункті 1 f(x0) = f(-2) = -2
та пункті 3 : f’(x0 ) = fʹ(-2) = -3 значення в рівняння дотичної у =fʹ(x0)(х – х0) + f(x0)
у = -3 · ( х –(-2)) -2, у = -3 х – 6 - 2, у = -3 х – 8
Відповідь: у = -3 х – 8
ПРИКЛАД 1