Содержание
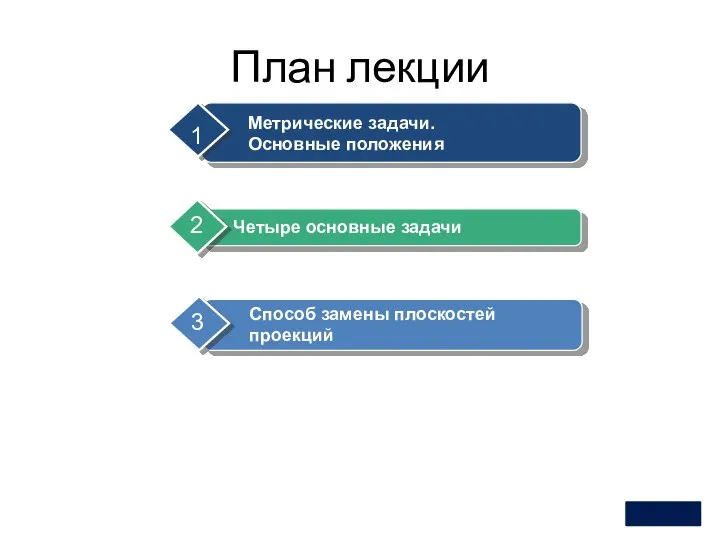
- 2. План лекции 1
- 3. Метрические задачи. Основные положения Метрические задачи - это задачи связанные с измерением, а именно,на определение натуральной
- 4. Метрические задачи. Основные положения Метрические задачи решаются не только в теоретических исследованиях, но и в прикладных
- 5. Метрические задачи. Основные положения Естественно полагать, что в общем случае заданные проекции не представляют натуральную величину.
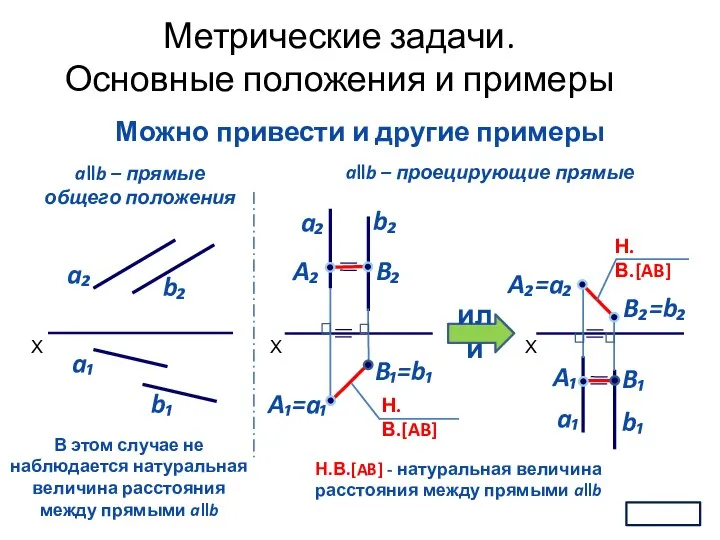
- 6. Метрические задачи. Основные положения и примеры Однако, при изучении свойств ортогонального проецирования отметили, если прямая параллельна
- 7. Метрические задачи. Основные положения и примеры Можно привести и другие примеры X a₁ b₁ a₂ b₂
- 8. Метрические задачи. Основные положения 2 Таким образом, решение метрических задач значительно облегчается, когда заданные геометрические объекты
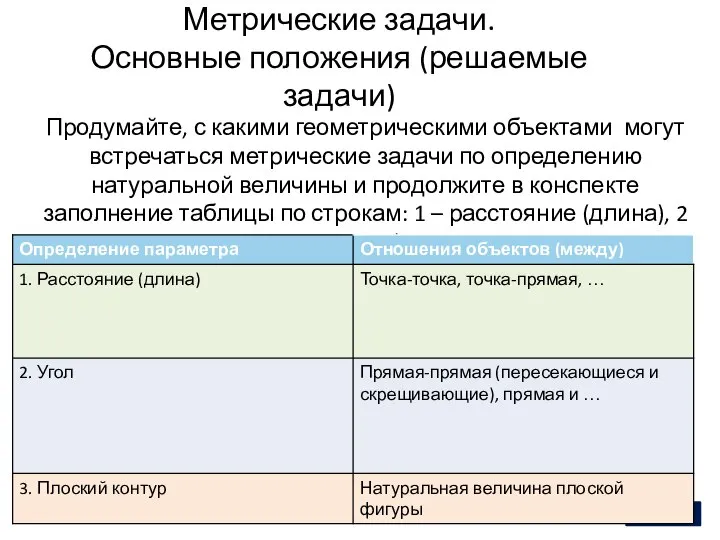
- 9. Метрические задачи. Основные положения (решаемые задачи) 2 Продумайте, с какими геометрическими объектами могут встречаться метрические задачи
- 10. Метрические задачи. Основные положения (основные задачи) 2 Все метрические задачи, решаются посредством определенного способа преобразования на
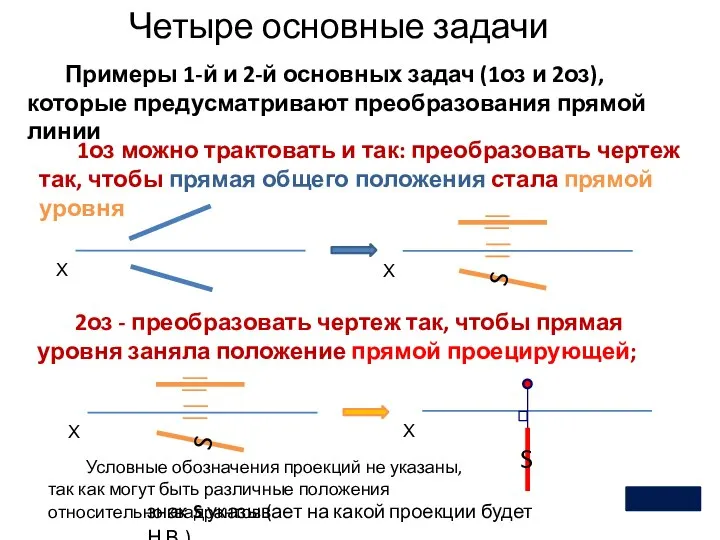
- 11. Четыре основные задачи 2 Примеры 1-й и 2-й основных задач (1оз и 2оз), которые предусматривают преобразования
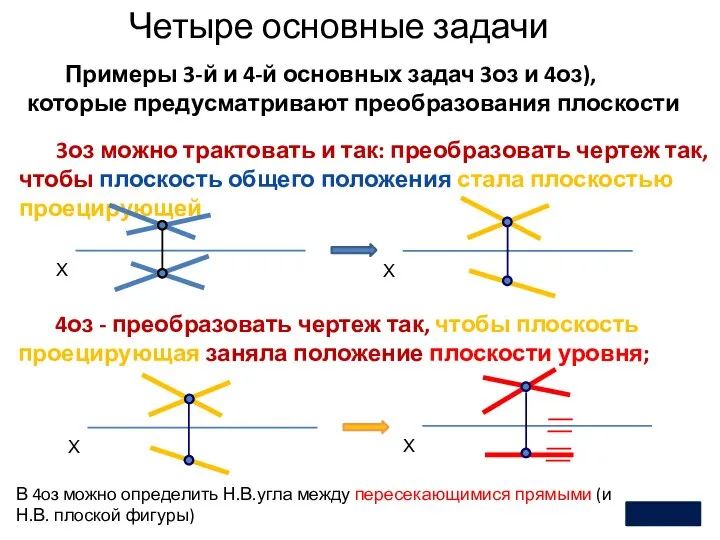
- 12. Четыре основные задачи 2 Примеры 3-й и 4-й основных задач 3оз и 4оз), которые предусматривают преобразования
- 13. Метрические задачи. Основные положения (три важных аспекта) 2 Таким образом, рассмотрим три очень важных аспекта, без
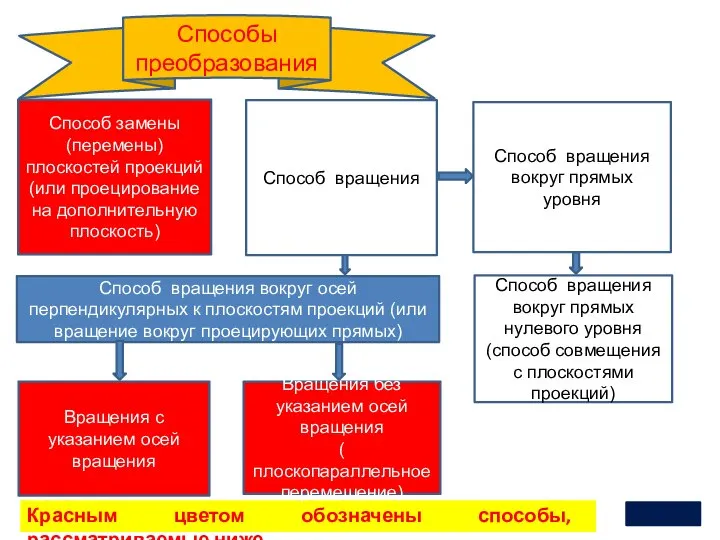
- 14. Метрические задачи. Основные положения (способы преобразования) 2 В соответствии с решением метрических задач можно подразделить такие
- 15. 2 Красным цветом обозначены способы, рассматриваемые ниже Способ замены (перемены) плоскостей проекций (или проецирование на дополнительную
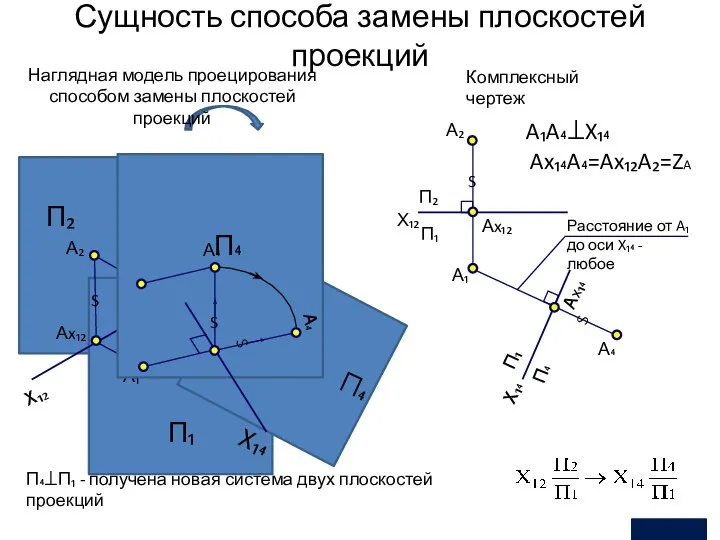
- 16. Способ замены плоскостей проекций заключается в замене одной из плоскостей проекций на другую (новую) плоскость проекций,
- 17. Сущность способа замены плоскостей проекций П₂ П₁ A₁ A Ax₁₄ S S П₄ X₁₄ S S
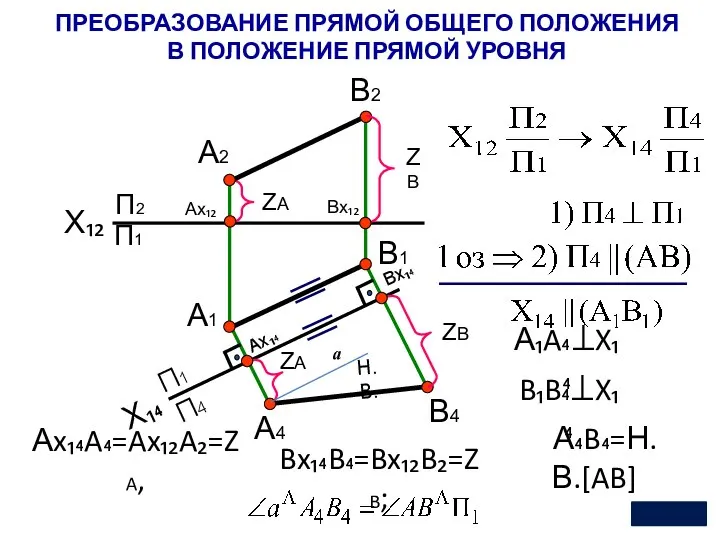
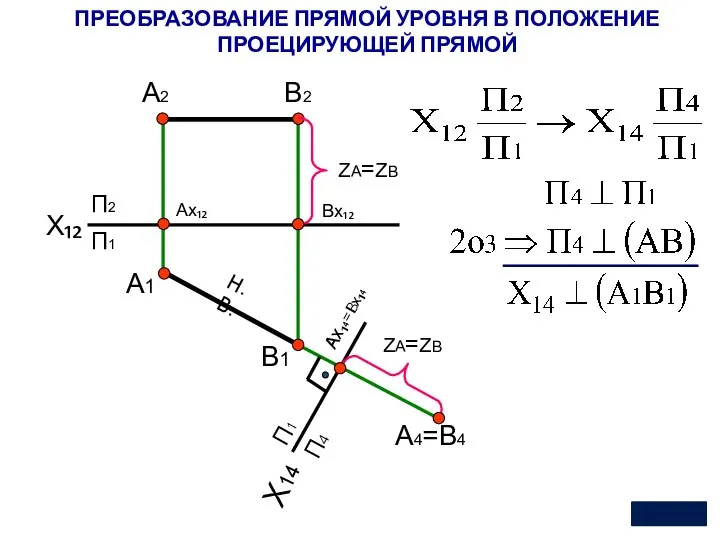
- 18. ПРЕОБРАЗОВАНИЕ ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ В ПОЛОЖЕНИЕ ПРЯМОЙ УРОВНЯ X₁₂ П2 Х₁₄ П1 П4 А1 А2 ZА
- 19. X₁₂ П2 Х14 П1 П4 А1 А2 А4=В4 В1 В2 П1 ZА=ZВ ZА=ZВ Н.В. 9 ПРЕОБРАЗОВАНИЕ
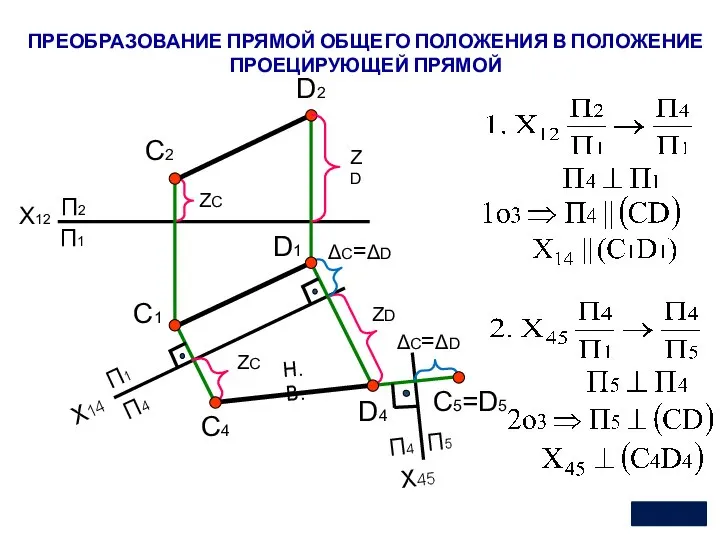
- 20. Преобразование чертежа прямой Прямая общего положения может быть последовательно преобразована в прямую уровня, и только затем,
- 21. X12 П2 Х14 П1 П4 C1 С2 ZC ZC D4 D1 D2 C4 П1 ZD ZD
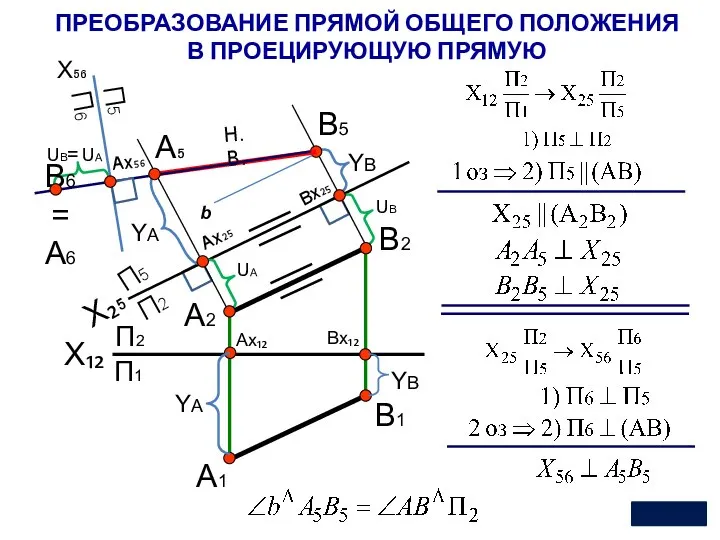
- 22. X₁₂ П2 П1 А1 А2 YА В1 В2 7 Ax₁₂ Bx₁₂ X₂₅ П5 П2 А₅ В5
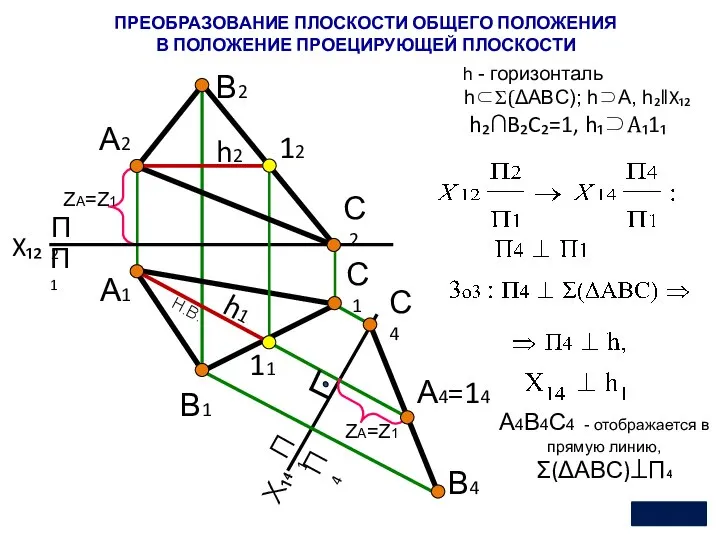
- 23. в положение проецирующей плоскости; Только затем в положение плоскости уровня. Преобразование чертежа плоскости Плоскость общего положения
- 24. П2 П1 П4 А4=14 П1 ZА=Z1 Н.В. X₁₂ А2 В2 А1 В1 С2 С1 12 11
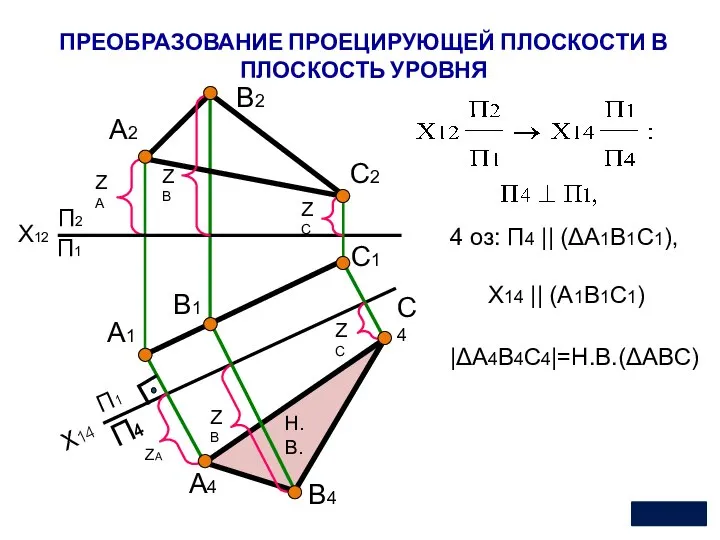
- 25. П2 Х14 П1 П4 А4 П1 ZА Н.В. X12 А2 В2 А1 С2 С1 |ΔA4B4C4|=Н.В.(ΔABC) В4
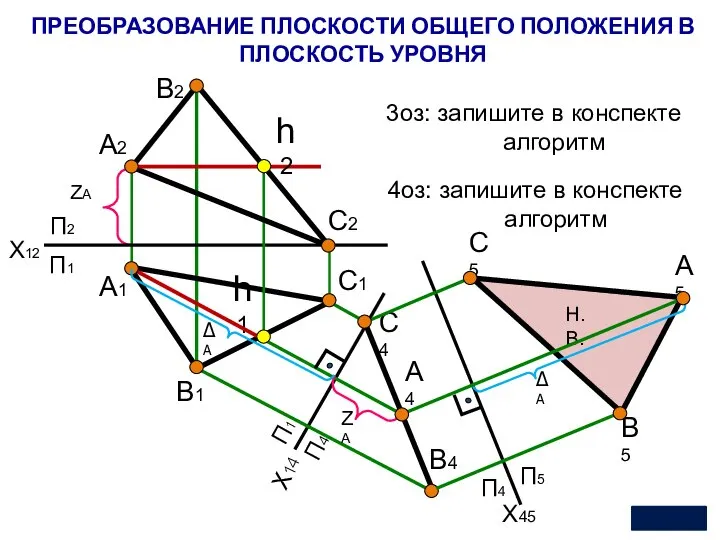
- 26. П2 Х14 П1 П4 А4 П1 ZА А2 В2 А1 В1 С2 С1 h2 h1 3оз:
- 28. Скачать презентацию











 Credit and exam
Credit and exam Создание геометрических тел
Создание геометрических тел Переход от передаточных функций к дифференциальным уравнениям и структурным схемам
Переход от передаточных функций к дифференциальным уравнениям и структурным схемам Поверхности второго порядка
Поверхности второго порядка Решение задач по теории вероятности. Подготовка к ГИА
Решение задач по теории вероятности. Подготовка к ГИА Старинные русские меры длины
Старинные русские меры длины Сочетания. В чем отличие от размещений?
Сочетания. В чем отличие от размещений? Устный счет
Устный счет Основы теории графов
Основы теории графов Урок математики в 1 классе
Урок математики в 1 классе Сравнение десятичных дробей
Сравнение десятичных дробей Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ
Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ  Педагогические приемы включения детей, имеющих нарушения слуха, в образовательное пространство урока математики
Педагогические приемы включения детей, имеющих нарушения слуха, в образовательное пространство урока математики Система MatLab/ Методические указания к выполнению лабораторных работ
Система MatLab/ Методические указания к выполнению лабораторных работ Рисование узора из геометрических фигур
Рисование узора из геометрических фигур Треугольники в окружающем мире
Треугольники в окружающем мире Метод группировки
Метод группировки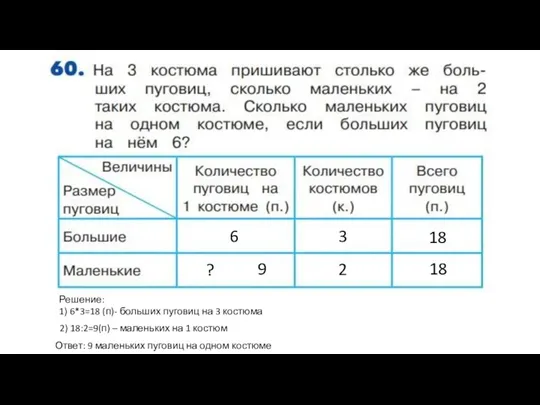 Задача о костюмах
Задача о костюмах Основы теории оболочек вращения
Основы теории оболочек вращения Знакомство с цифрой 5
Знакомство с цифрой 5 Линии и углы в окружности
Линии и углы в окружности Формирование знаковой культуры на уроках
Формирование знаковой культуры на уроках Статистическое наблюдение
Статистическое наблюдение Формула Остроградского - Гаусса
Формула Остроградского - Гаусса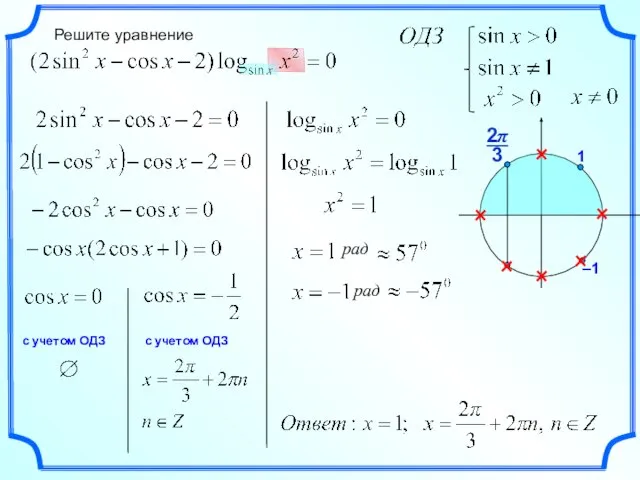 Решение уравнения
Решение уравнения Приемы устного счета
Приемы устного счета Вычисление неопределенного интеграла
Вычисление неопределенного интеграла Состав числа 10
Состав числа 10