Координаты вектора в пространстве. 12 кл

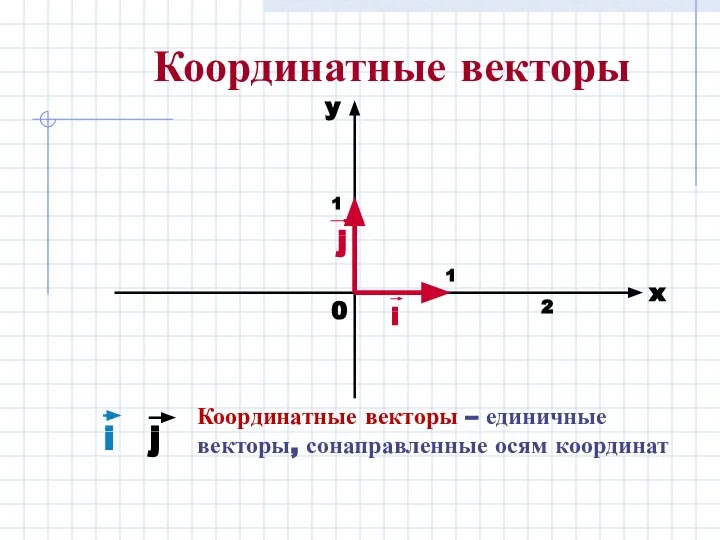
Координатные векторы
Координатные векторы – единичные векторы, сонаправленные осям координат

i – единичный вектор оси абсцисс, j – единичный вектор оси ординат, k – единичный вектор оси аппликат.
x
z
y
O
Координатные векторы

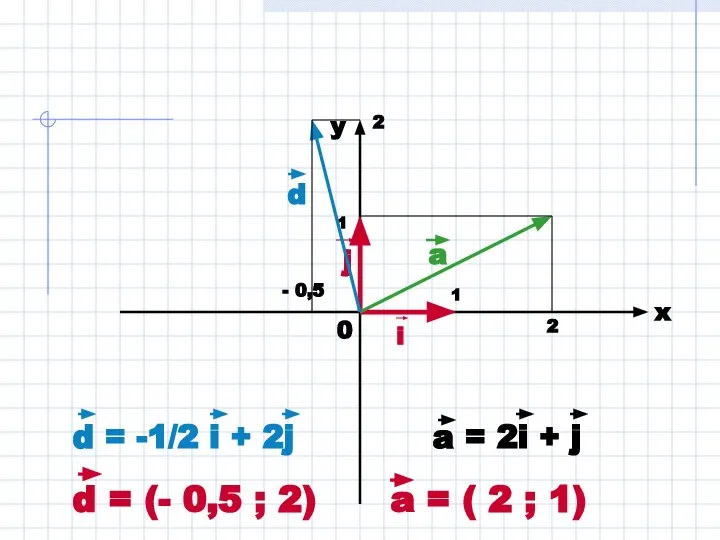
Координаты вектора
Числа X и Y называются координатами вектора

Любой вектор в пространстве a можно разложить по координатным векторам, т.е. представить в виде суммы:
Нулевой вектор можно представить в виде:
Координаты вектора

Координаты вектора
Числа X, Y и Z называются координатами вектора

Длина вектора
Длина вектора равна корню квадратному из суммы квадратов его координат.

Длина вектора
Длина вектора равна корню квадратному из суммы квадратов его координат.

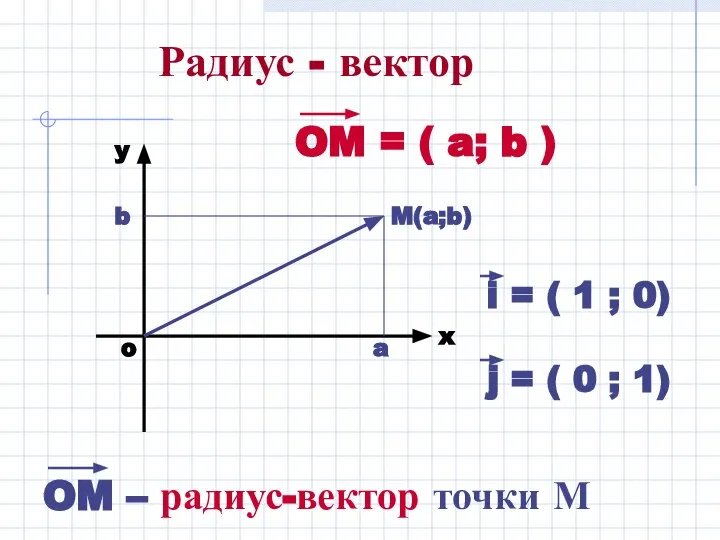
Радиус - вектор
M(a;b)
a
b

Вектор, конец которого совпадает с данной точкой, а начало – с началом координат, называется радиус-вектором данной точки.
Координаты любой точки равны соответствующим координатам её радус-вектора.
М (x; y; z)
OM =(x; y; z)
Радиус - вектор
j = ( 0 ; 1 ; 0)

Равенство векторов
Векторы равны, если равны их соответствующие координаты.
X1 = X2
Y1 = Y2

Равенство векторов
Векторы равны, если равны их соответствующие координаты.
X1 = X2
Y1 = Y2
Z1 = Z2

Cумма векторов
Если a = (X1; Y1) и
b = (X2; Y2) , то
a + b = (X1 + X2 ; Y1 + Y2)
Координаты суммы векторов равны суммам соответствующих координат слагаемых.

Cумма векторов
Если a = (X1 ; Y1 ; Z1 ) и
b = (X2 ; Y2 ; Z2), то
a + b = (X1 + X2 ; Y1 + Y2 ; Z1 + Z2)
Координаты суммы векторов равны суммам соответствующих координат слагаемых.

Разность векторов
Если a = (X1; Y1) и
b = (X2; Y2) , то
a - b = (X1 - X2 ; Y1 - Y2)
Координаты разности двух векторов равны разностям соответствующих координат уменьшаемого и вычитаемого.

Разность векторов
Если a = (X1 ; Y1 ; Z1 ) и
b = (X2 ; Y2 ; Z2), то
a - b = (X1 - X2 ; Y1 - Y2 ; Z1 - Z2)
Координаты разности двух векторов равны разностям соответствующих координат уменьшаемого и вычитаемого.

Произведение вектора на число.
Если a = (X; Y), то
ka = (kX; kY).
Чтобы умножить вектор на число, нужно умножить на это число каждую из координат вектора.

Произведение вектора на число.
Если a = (X ; Y ; Z ), то
ka = (kX; kY; kZ).
Чтобы умножить вектор на число, нужно умножить на это число каждую из координат вектора.

Произведение вектора на число.
Если a = (X ; Y), то
- a = (-X ; -Y).
Координаты противоположного вектора противоположны координатам данного вектора.

Произведение вектора на число.
Если a = (X ; Y ; Z ), то
- a = (-X ; -Y ; -Z).
Координаты противоположного вектора противоположны координатам данного вектора.

Скалярное произведение векторов:
Если a = (X1; Y1) и
b = (X2; Y2) , то