Содержание
- 2. Цель урока: Обеспечение усвоения понятия корня натуральной степени из числа. Формирование представлений о свойствах корней и
- 3. Корнем n – й степени из действительного числа a (n – натуральное число) называют такое действительное
- 4. Операция извлечения корня является обратной по отношению к возведению в соответствующую степень. 5² = 25 10³
- 5. Пример 1: Вычислить: а) √ 49; б) √ 0,125; в) √ 0 ; г) √ 17
- 6. Корень чётной степени имеет смысл (т.е. определён) только для неотрицательного подкоренного выражения; корень нечётной степени имеет
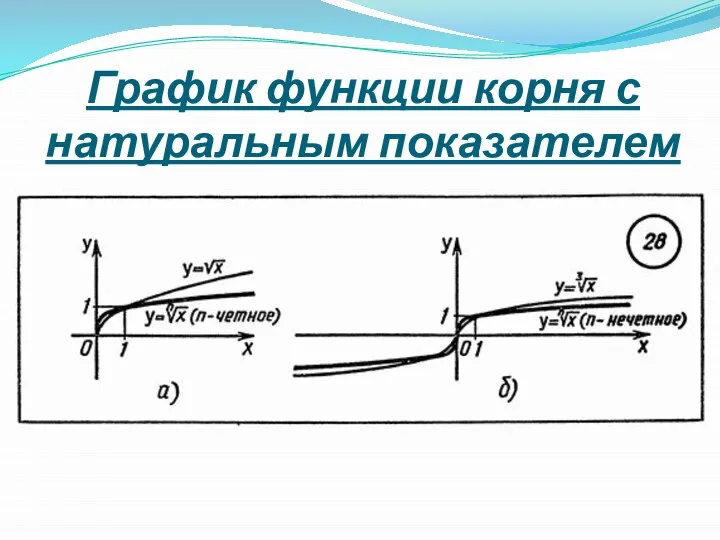
- 7. График функции корня с натуральным показателем
- 8. самостоятельно
- 9. 1.Корень n-степени (n=2,3,4,5, …) из произведения неотрицательных чисел равен произведению корней n-степени из этих чисел: =
- 10. 2. Чтобы извлечь корень из дроби, нужно извлечь корень из числителя и знаменателя отдельно и первый
- 11. 3. Если a≥0, n=2,3,4,5,… и k – любое натуральное число, то справедливо равенство: Пример:
- 12. 4. Если a≥0, n и k - натуральные числа, большие 1, то справедливо равенство: Пример:
- 13. 5. Если показатели корня и подкоренного выражения умножить или разделить на одно и то же отличное
- 14. 6. Чтобы извлечь корень из степени, показатель которой делится на показатель корня, нужно показатель степени разделить
- 15. Приближенные значения корней умели находить еще жители древнего Вавилона около 4 тысяч лет назад. Не имея
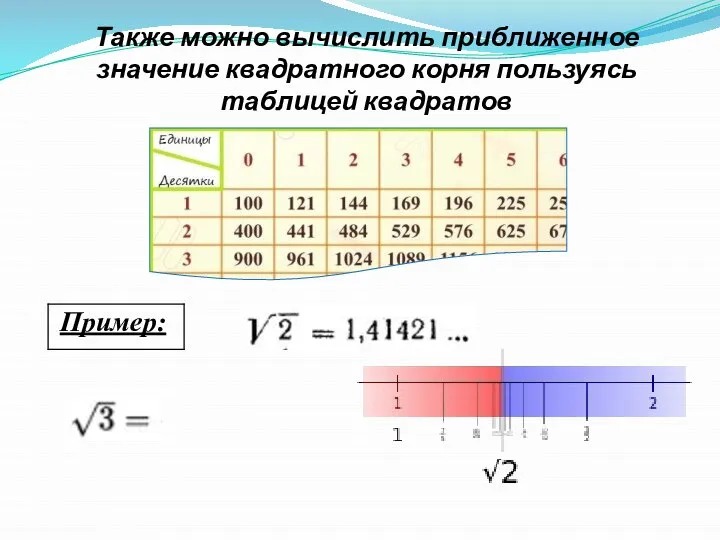
- 16. Также можно вычислить приближенное значение квадратного корня пользуясь таблицей квадратов
- 19. Скачать презентацию














 Определение арифметической прогрессии
Определение арифметической прогрессии Значение степени возведение в степень
Значение степени возведение в степень Задание 19. Профиль (1)
Задание 19. Профиль (1) Анализ и синтез как методы научного познания, их применение при обучении математике
Анализ и синтез как методы научного познания, их применение при обучении математике Погрешность измерения
Погрешность измерения Презентация на тему Параллелограмм и трапеция
Презентация на тему Параллелограмм и трапеция  “Збери” задачу
“Збери” задачу Решение задач на применение свойств прямоугольного треугольника. 7 класс
Решение задач на применение свойств прямоугольного треугольника. 7 класс Нелинейная парная регрессия
Нелинейная парная регрессия Теорема синусов
Теорема синусов Решение практических задач с применением вероятностных методов
Решение практических задач с применением вероятностных методов Система MatLab. Методические указания к выполнению лабораторных работ
Система MatLab. Методические указания к выполнению лабораторных работ Векторы в пространстве
Векторы в пространстве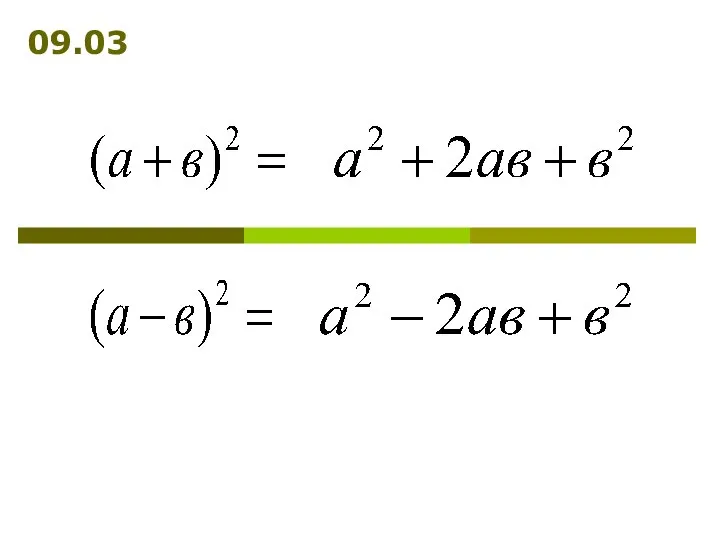 Преобразование многочленов с помощью формул сокращённого умножения
Преобразование многочленов с помощью формул сокращённого умножения Подготовка к ВПР. Равенство
Подготовка к ВПР. Равенство Делимость чисел. НОК
Делимость чисел. НОК Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Свойства степени
Свойства степени Угол между прямыми в пространстве
Угол между прямыми в пространстве Признаки равенства треугольников. Подготовка к контрольной работе
Признаки равенства треугольников. Подготовка к контрольной работе Комплексные числа. Все формы
Комплексные числа. Все формы Работа над ошибками СОР. Подготовка к СОЧ
Работа над ошибками СОР. Подготовка к СОЧ Что узнали. Чему научились
Что узнали. Чему научились Примеры комбинаторных задач
Примеры комбинаторных задач Презентация на тему УСТНЫЙ СЧЕТ
Презентация на тему УСТНЫЙ СЧЕТ  Презентация на тему Объём прямоугольного параллелепипеда
Презентация на тему Объём прямоугольного параллелепипеда  Решение задач на применение свойств прямоугольного треугольника
Решение задач на применение свойств прямоугольного треугольника Сложение векторов
Сложение векторов