Слайд 2Назначение критерия
Критерий применяется в случае, когда стоит задача сравнить средние показатели двух

распределений.
Слайд 3Ограничения критерия
Распределения должны быть нормальными.
n≥2

Слайд 4Эмпирическое значение критерия вычисляется по формуле:
│Xср1-Хср2│
t = ---------------
√m12+ m22
m -

ошибка среднего,
Хср - средние арифметическое значение,
n – объем соответствующей выборки.
Слайд 5Среднее арифметическое значение
Это сумма всех значений выборки, поделенная на количество этих

значений.
Обозначается Хср и вычисляется по формуле:
хi- i-е значение выборки;
i – порядковый номер значения в выборке;
n – объем выборки.
Слайд 6Пример нахождения среднего арифметического значения

Слайд 7формула для случая, когда значения повторяются.
yi – i-я варианта выборки,
fi – частота

i-й варианты,
k – количество вариант.
Слайд 8Дисперсия
мера разброса данных вокруг среднего арифметического значения. Обозначается S2x и вычисляется по

формуле:
Слайд 9Стандартное отклонение
данная мера тесно связана с дисперсией, так как является квадратным корнем

из нее. Обозначается σ и вычисляется по формуле:
Слайд 10Пример расчета по t- критерию
Различаются ли по средним значениям
студенты с низким

и высоким учебным
стрессом по ситуативной тревожности,
измеренной по методике Спилберга.
Слайд 13Значение критерия
│40,1-43,2│
t = --------------- = 1,05
√4,76+3,92

Слайд 14Гипотезы
Н1: Студенты с высоким учебным стрессом по среднему значению ситуативной тревожности значимо

превосходят студентов с низким учебным стрессом
Н0: Студенты с высоким и низким учебным стрессом по среднему значению ситуативной тревожности статистически не различаются













 Олимпиадная математика (начальная школа)
Олимпиадная математика (начальная школа) Логарифм произведения
Логарифм произведения Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве Презентация на тему Графическое решение квадратных уравнений (8 класс)
Презентация на тему Графическое решение квадратных уравнений (8 класс)  Параллельные алгоритмы вычислительной алгебры. Распараллеливание на компьютерах с распределенной памятью
Параллельные алгоритмы вычислительной алгебры. Распараллеливание на компьютерах с распределенной памятью Математическое моделирование. Контурно-графический анализ
Математическое моделирование. Контурно-графический анализ Римские цифры. 3 класс
Римские цифры. 3 класс Вычисление площадей плоских фигур
Вычисление площадей плоских фигур Методика эконометрических исследований
Методика эконометрических исследований Угол
Угол Презентация Понономарев
Презентация Понономарев Укрупненные единицы счета
Укрупненные единицы счета Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20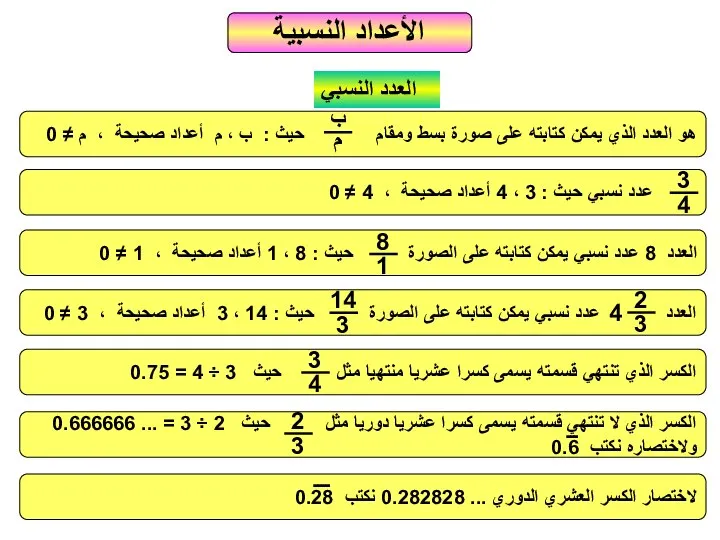 الأعداد انسبية
الأعداد انسبية Многогранники. Вершины, рёбра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера
Многогранники. Вершины, рёбра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера Многоугольники
Многоугольники Внимание: свойства, функции и виды
Внимание: свойства, функции и виды ЛP№1_Симплекс-метод окон
ЛP№1_Симплекс-метод окон Комбинаторные задачи. 9 класс
Комбинаторные задачи. 9 класс Математика вокруг нас
Математика вокруг нас Практика 2_ИВМО-04-22_Куликова_Кластерный анализ
Практика 2_ИВМО-04-22_Куликова_Кластерный анализ 20b
20b Показательные уравнения
Показательные уравнения Математическое моделирование
Математическое моделирование Модели представления задач
Модели представления задач Решение уравнений. Первый и второй уровни
Решение уравнений. Первый и второй уровни Треугольные узоры. Правильный треугольник
Треугольные узоры. Правильный треугольник Построение графиков функций
Построение графиков функций