Содержание
- 2. Движение плоскости – это отображение плоскости на себя, сохраняющее расстояния. ДВИЖЕНИЕ ВИДЫ ДВИЖЕНИЯ
- 3. ИСТОРИЯ СИММЕТРИИ Ещё древние греки считали, что симметрия – это гармония, соразмерность, они же и ввели
- 4. Слово симметрия в переводе с древнегреческого языка – это «соразмерность». Под симметрией в широком смысле этого
- 5. ОСЕВАЯ СИММЕТРИЯ Преобразование, при котором каждая точка А фигуры (или тела) преобразуется в симметричную ей относительно
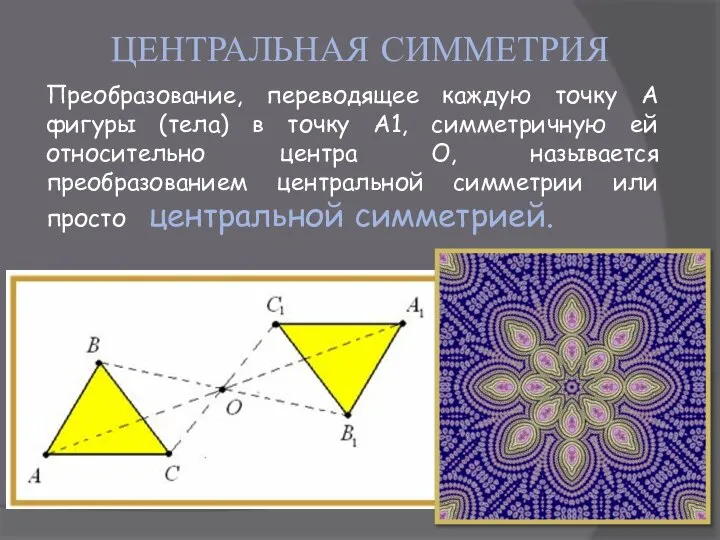
- 6. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ Преобразование, переводящее каждую точку А фигуры (тела) в точку А1, симметричную ей относительно центра
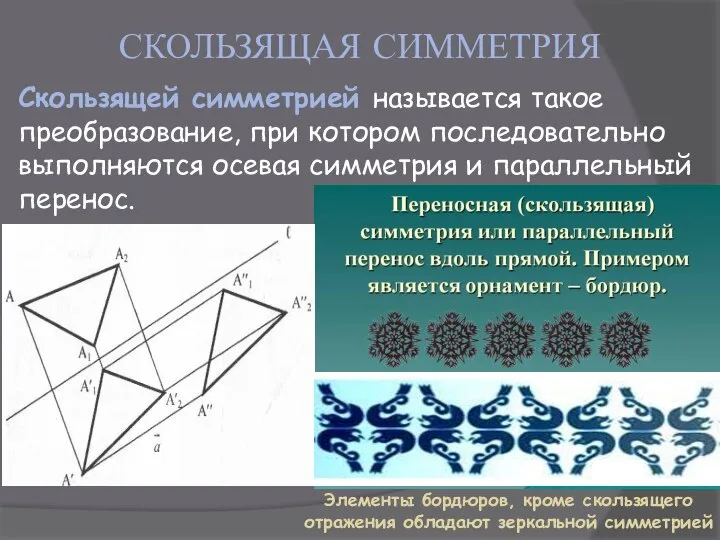
- 7. СКОЛЬЗЯЩАЯ СИММЕТРИЯ Скользящей симметрией называется такое преобразование, при котором последовательно выполняются осевая симметрия и параллельный перенос.
- 8. ЗЕРКАЛЬНАЯ СИММЕТРИЯ Если преобразование симметрии относительно плоскости переводит фигуру (тело) в себя, то фигура называется симметричной
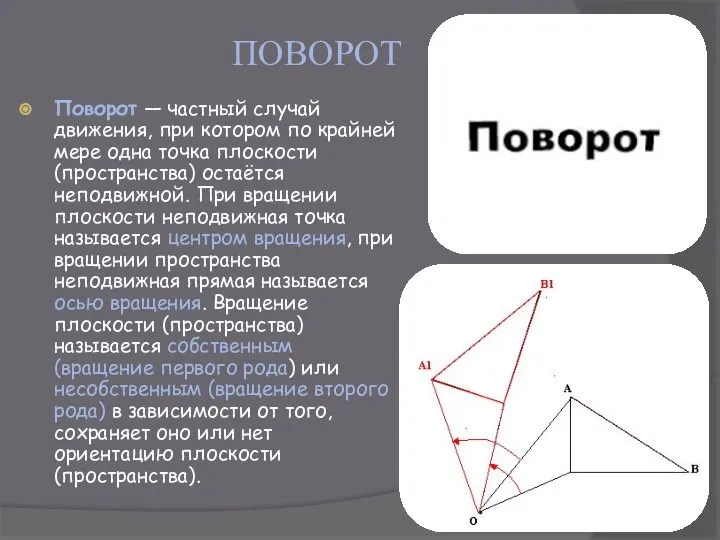
- 9. ПОВОРОТ Поворот — частный случай движения, при котором по крайней мере одна точка плоскости (пространства) остаётся
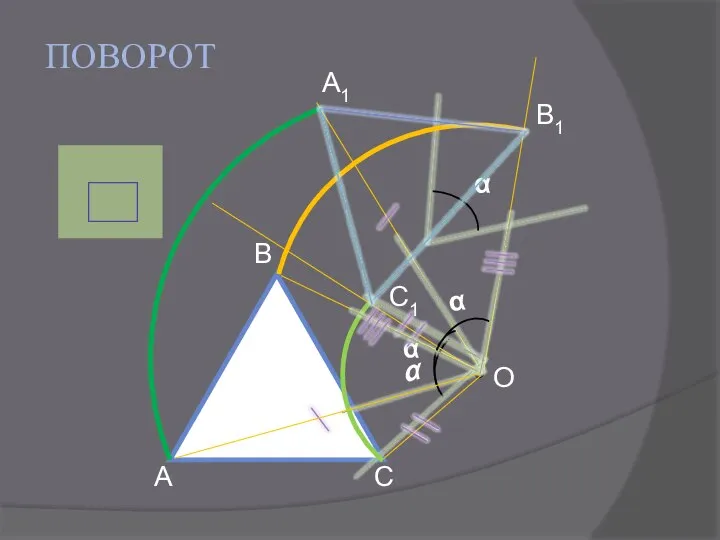
- 10. ПОВОРОТ О А1 В1 С1 ?
- 11. Вывод: Чтобы получить отображение фигуры при повороте около данной точки, нужно каждую точку фигуры повернуть на
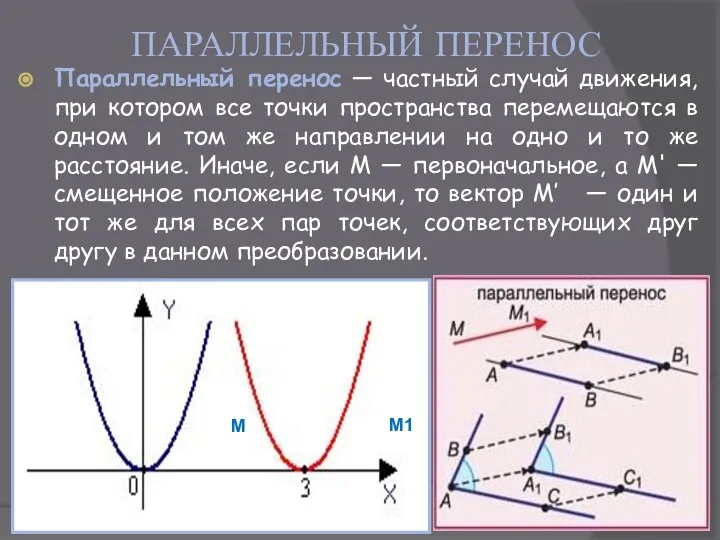
- 12. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС Параллельный перенос ― частный случай движения, при котором все точки пространства перемещаются в одном
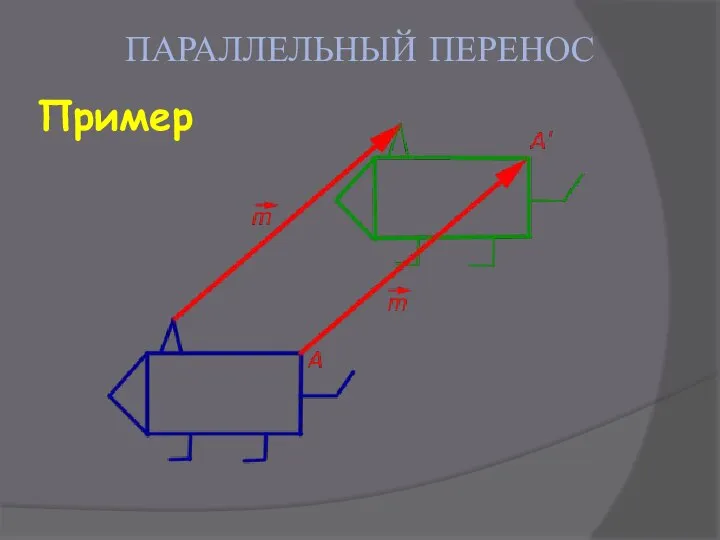
- 13. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС Пример
- 14. РОЛЬ СИММЕТРИИ В МИРЕ Как бы нам жилось без симметрии? Какую роль играет симметрия в нашем
- 15. СИММЕТРИЯ В ОКРУЖАЮЩЕМ НАС МИРЕ
- 16. Заключение ДВИЖЕНИЕ И ВСЕ ЕГО ВИДЫ ЯВЛЯЮТСЯ НЕОТЪЕМЛЕМОЙ И ВАЖНОЙ КОМПОНЕНТОЙ СУЩЕСТВОВАНИЯ ЧЕЛОВЕЧЕСТВА. БЕЗ ДВИЖЕНИЙ НЕ
- 18. Скачать презентацию









 Решение неравенств второй степени с помощью эскиза параболы
Решение неравенств второй степени с помощью эскиза параболы Интегрированный урок информатики и алгебры
Интегрированный урок информатики и алгебры Задачи с параметром на ЕГЭ (задача 18). Линейные уравнения
Задачи с параметром на ЕГЭ (задача 18). Линейные уравнения Презентация на тему Поле чудес по математике
Презентация на тему Поле чудес по математике  Объёмы геометрических тел
Объёмы геометрических тел Теория вероятности. Задачи. 9 класс
Теория вероятности. Задачи. 9 класс Решение уравнений, содержащих модуль
Решение уравнений, содержащих модуль Презентация на тему Август Фердинанд Мёбиус
Презентация на тему Август Фердинанд Мёбиус  Приемы устных вычислений в пределах 100. 3 класс
Приемы устных вычислений в пределах 100. 3 класс Комплексные числа
Комплексные числа МО26
МО26 Квадратные уравнения
Квадратные уравнения Признаки параллельности прямых
Признаки параллельности прямых Построение треугольника по трем сторонам
Построение треугольника по трем сторонам Стереометрия. Основные фигуры в пространстве
Стереометрия. Основные фигуры в пространстве Числовые неравенства
Числовые неравенства Презентация на тему ЭКСТРЕМУМЫ ФУНКЦИИ
Презентация на тему ЭКСТРЕМУМЫ ФУНКЦИИ  Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Задача о трех игральных костях. Элементарный способ
Задача о трех игральных костях. Элементарный способ Повторение. Решение систем линейных уравнений с двумя переменными
Повторение. Решение систем линейных уравнений с двумя переменными Тригонометрические уравнения. Однородные тригонометрические уравнения
Тригонометрические уравнения. Однородные тригонометрические уравнения Презентация на тему Площадь четырёхугольника
Презентация на тему Площадь четырёхугольника  Числа от 1 до 7. Письмо цифры 7. Познакомить с числом 7. Образованием числа 7
Числа от 1 до 7. Письмо цифры 7. Познакомить с числом 7. Образованием числа 7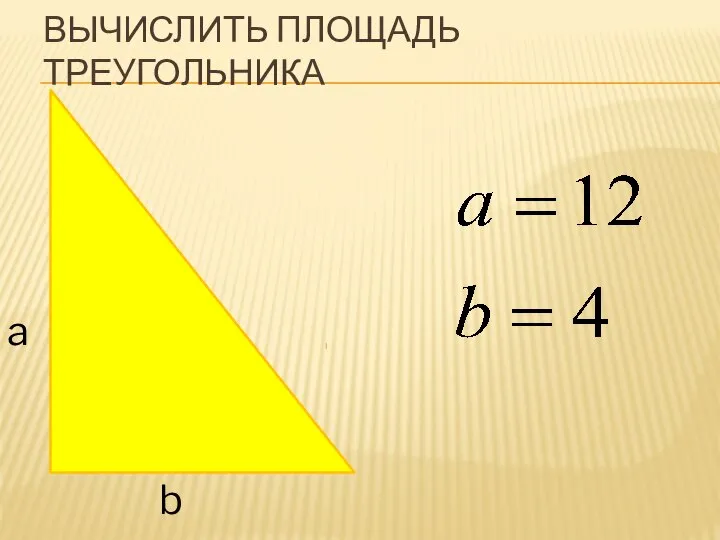 Вычисление площади треугольника
Вычисление площади треугольника Веселый счет (Счет в прямом и обратном порядке в пределах 10)
Веселый счет (Счет в прямом и обратном порядке в пределах 10) Квадратный корень из степени
Квадратный корень из степени Формулы для решения С2 координатно-векторным способом
Формулы для решения С2 координатно-векторным способом Метод Галеркина для дифференциально-операторного уравнения третьего порядка
Метод Галеркина для дифференциально-операторного уравнения третьего порядка