Функция. Свойства функции. График функции

«Функция, как правило, определяется для тех
значений аргумента, какие для данной задачи
представляют реальное значение».
(А. Я. Хинчин)

Цель:
повторить определение функции,
способы ее задания;
повторить общие свойства функции;
совершенствовать навык чтения
графиков функциональной зависимости.

1. Что такое функция?
Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.
2. Как можно задать функцию?
Функцию можно задать аналитически (формулой, таблицей) и графически.
3. Что называют графиком функции?
Графиком функции называют множество всех точек, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.

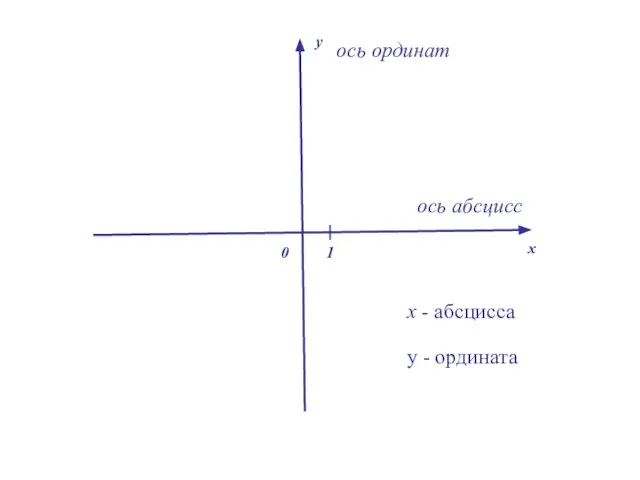
1
0
х
у
х - абсцисса
у - ордината
ось абсцисс
ось ординат

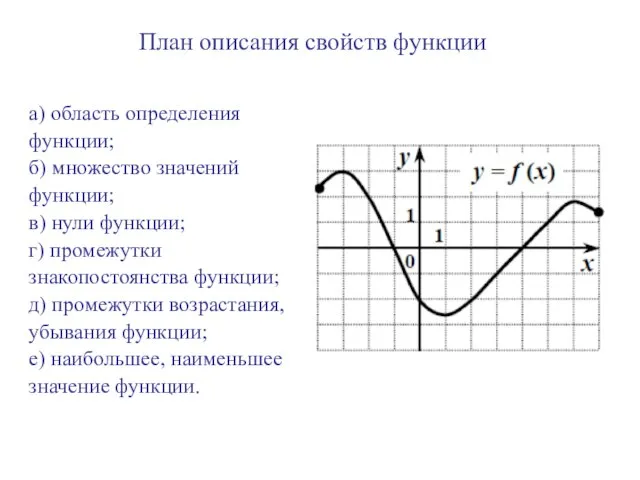
а) область определения
функции;
б) множество значений
функции;
в) нули функции;
г) промежутки
знакопостоянства функции;
д) промежутки возрастания,
убывания функции;
е) наибольшее, наименьшее
значение функции.
План описания свойств функции

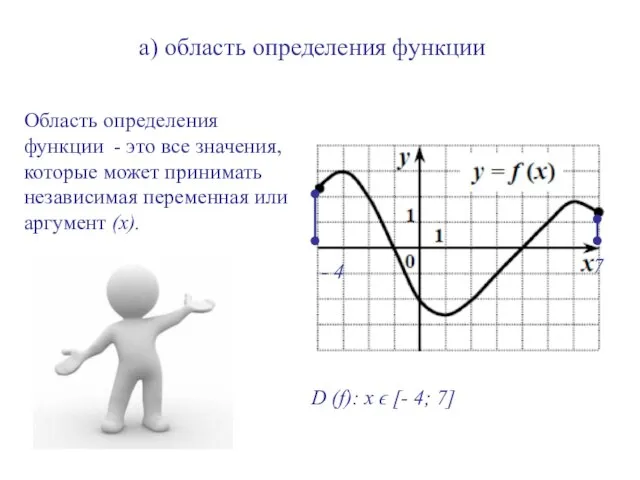
а) область определения функции
Область определения функции - это все значения, которые может принимать независимая переменная или аргумент (х).
- 4
7
D (f): x ϵ [- 4; 7]

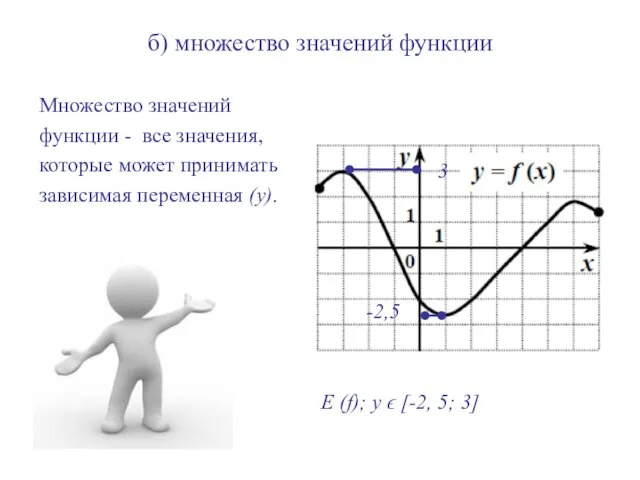
б) множество значений функции
Множество значений
функции - все значения,
которые может принимать
зависимая переменная (у).
-2,5
3
E (f); y ϵ [-2, 5; 3]

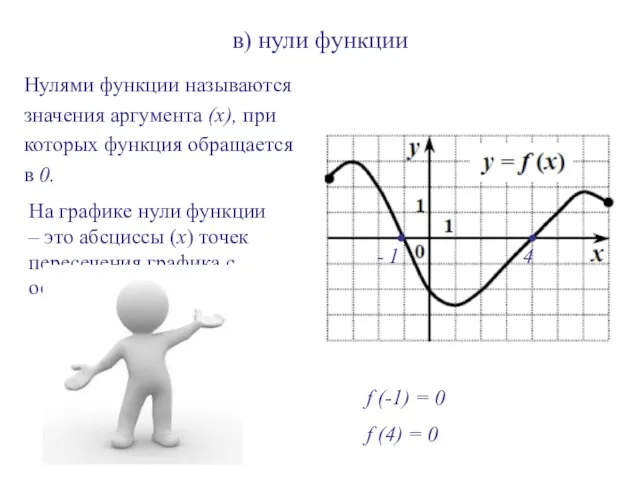
в) нули функции
Нулями функции называются
значения аргумента (х), при
которых функция обращается
в 0.
На графике нули функции – это абсциссы (х) точек пересечения графика с осью х
●
- 1
●
4
f (-1) = 0
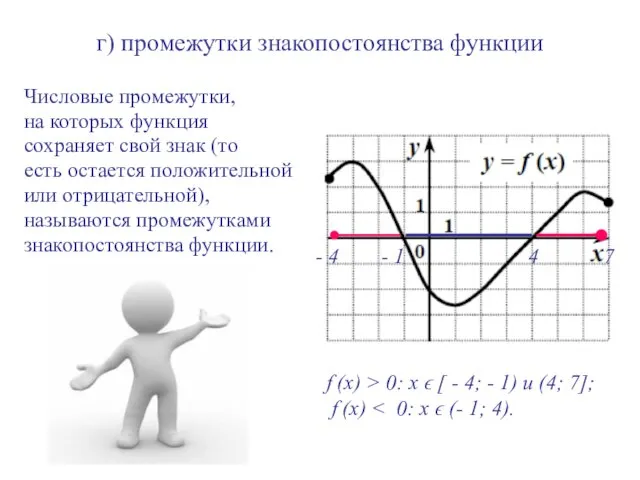
f (4) = 0

г) промежутки знакопостоянства функции
Числовые промежутки,
на которых функция
сохраняет свой знак (то
есть остается положительной
или отрицательной),
называются промежутками
знакопостоянства функции.
- 4
- 1
4
7
f (x) > 0: х ϵ [ - 4; - 1) и (4; 7];
f (x) < 0: х ϵ (- 1; 4).

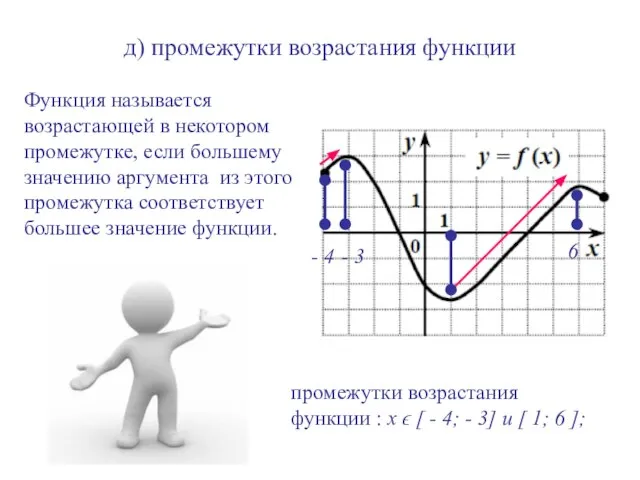
д) промежутки возрастания функции
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.
- 4
- 3
6
промежутки возрастания функции : х ϵ [ - 4; - 3] и [ 1; 6 ];

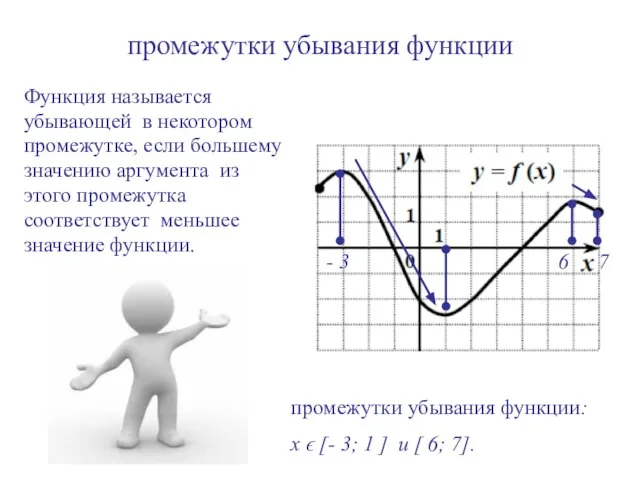
промежутки убывания функции
Функция называется
убывающей в некотором
промежутке, если большему
значению аргумента из
этого промежутка
соответствует меньшее
значение функции.
промежутки убывания функции:
х ϵ [- 3; 1 ] и [ 6; 7].
- 3
6
7

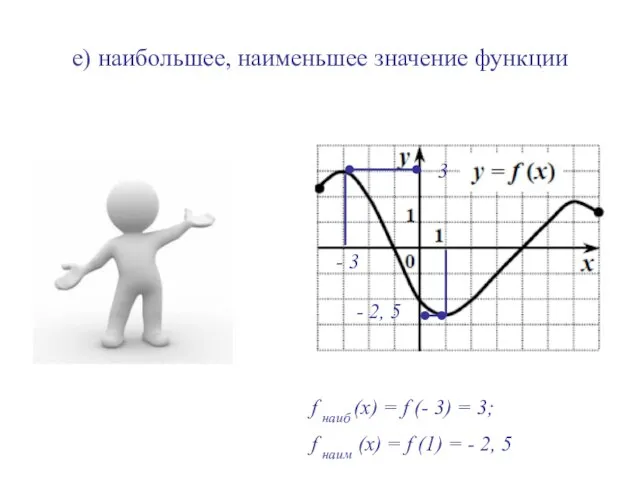
е) наибольшее, наименьшее значение функции
- 2, 5
3
f наиб (х) = f (- 3) = 3;
f наим (х) = f (1) = - 2, 5
- 3

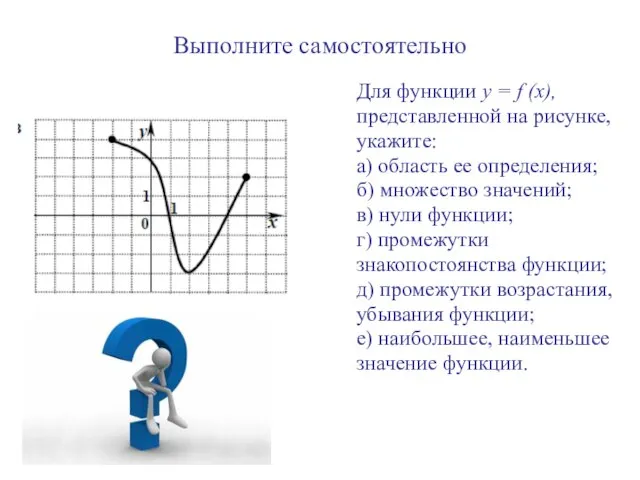
Выполните самостоятельно
Для функции y = f (x),
представленной на рисунке,
укажите:
а) область ее определения;
б) множество значений;
в) нули функции;
г) промежутки
знакопостоянства функции;
д) промежутки возрастания,
убывания функции;
е) наибольшее, наименьшее
значение функции.