Комплексные числа

22.1. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ
НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ
Комплексным числом называется выражение вида
где х и у – действительные числа,
i – мнимая единица:

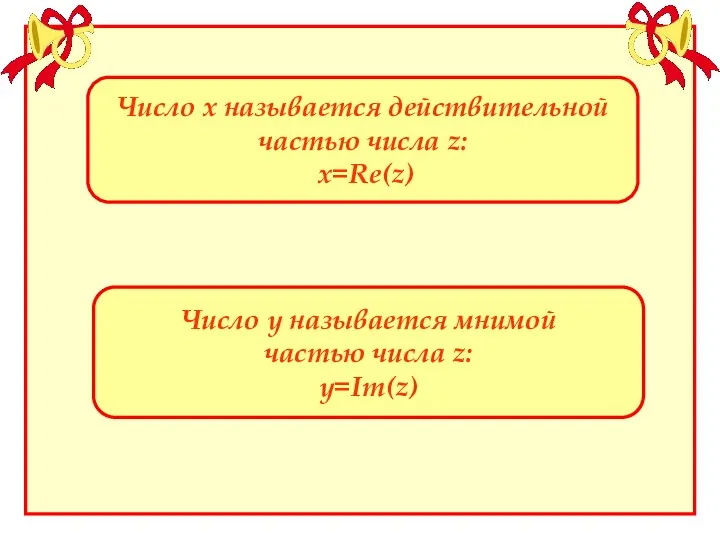
Число х называется действительной
частью числа z:
х=Re(z)
Число у называется мнимой
частью числа z:
у=Im(z)

Действительное число х является частным случаем комплексного числа
при у=0.
Комплексные числа вида
не являющиеся действительными, т.е. при
называются мнимыми, а при
называются чисто мнимыми.

Комплексные числа
называются сопряженными
Комплексные числа
называются равными, если равны их действительные и мнимые части:

Арифметические действия
над множеством комплексныx чисел
1
Сумма (разность) комплексных чисел:

2
Произведение комплексных чисел:

Поскольку
Например:

3
Деление комплексных чисел:

Поскольку

Пример.
Найти сумму, разность, произведение
и частное комплексных чисел:

Решение

Если для изображения действительных чисел используются точки числовой прямой, то для изображения комплексных чисел используются точки координатной плоскости ХОУ.
Плоскость называется комплексной, если любому комплексному числу
ставятся в соответствие точки плоскости ХОУ, причем это соответствие взаимно однозначное.