Квадартные уравнения. Основные понятия

Цель урока:
получить понятие о квадратном уравнении, видах квадратных уравнений;
Получить навыки решения неполных квадратных уравнений.

Квадратным уравнением называют
уравнение вида
ax2 + bx + c = 0,
где х – неизвестное, a, b, c – числа,
a ≠ 0.
а – первый (старший) коэффициент
b – второй коэффициент
с – свободный член

Назовите коэффициенты
а, b, c в уравнении:
а) 4х2 + 5х + 7 = 0 б) 13х2 = 0
в) 8х2 – 3х + 4 = 0 г) 4х2 – 5 + х = 0
д) – 3х2 + х – 5 = 0 е) 5 – 6х + х2 = 0
ж) х2 – 4 = 0 з) 4 – 2х2 – х = 0
и) 3х2 – х = 0

Полное квадратное уравнение – это квадратное уравнение, в котором присутствуют все три слагаемых.
Неполное квадратное уравнение – это уравнение, в котором хотя бы один из коэффициентов b или с равен нулю:
если b = 0 ax2 + c = 0
если с = 0 ax2 + bx = 0
если b = c = 0 ax2 = 0

Корнем квадратного уравнения
ax2 + bx + c = 0
называют число, при подстановке которого вместо неизвестного в уравнение получается верное числовое равенство.
Решить квадратное уравнение – это значит найти все его корни или установить, что корней нет.

1 вид неполного квадратного уравнения

2 вид
неполного квадратного уравнения
3 вид
неполного квадратного уравнения

Если парабола
у = ax2 + bx + c
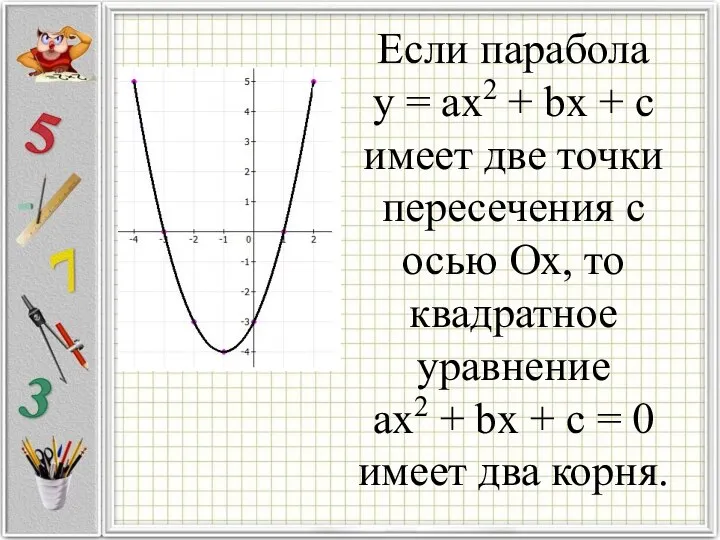
имеет две точки пересечения с осью Ох, то квадратное уравнение
ax2 + bx + c = 0
имеет два корня.

Если парабола
у = ax2 + bx + c
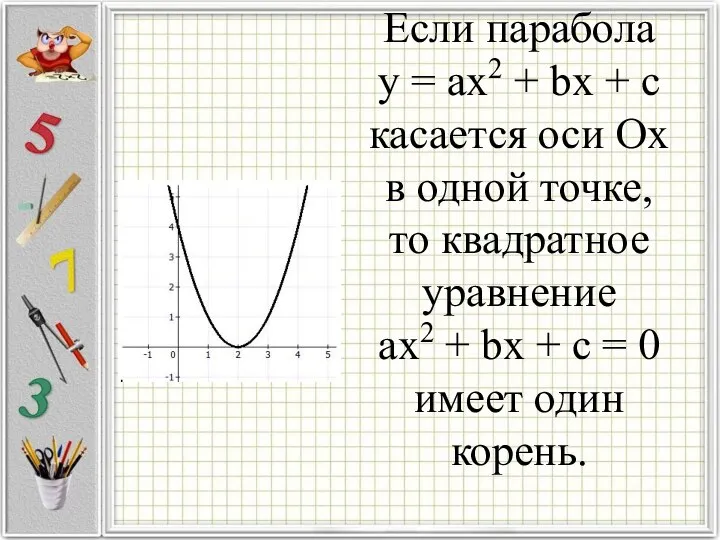
касается оси Ох в одной точке, то квадратное уравнение
ax2 + bx + c = 0
имеет один корень.

Если парабола
у = ax2 + bx + c
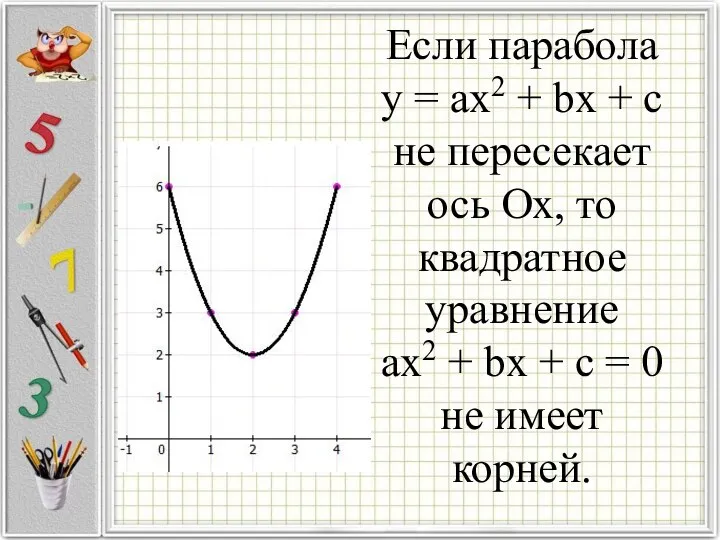
не пересекает ось Ох, то квадратное уравнение
ax2 + bx + c = 0
не имеет корней.