- Главная
- Математика
- Теория погрешностей

Содержание
- 2. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 3. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 4. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 5. №1 В Ы Ч И С Л И Т Е Л Ь Н А Я М
- 6. Специфика вычислительной математики Вычислительная математика имеет дело не только с непрерывными, но и с дискретными объектами
- 7. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
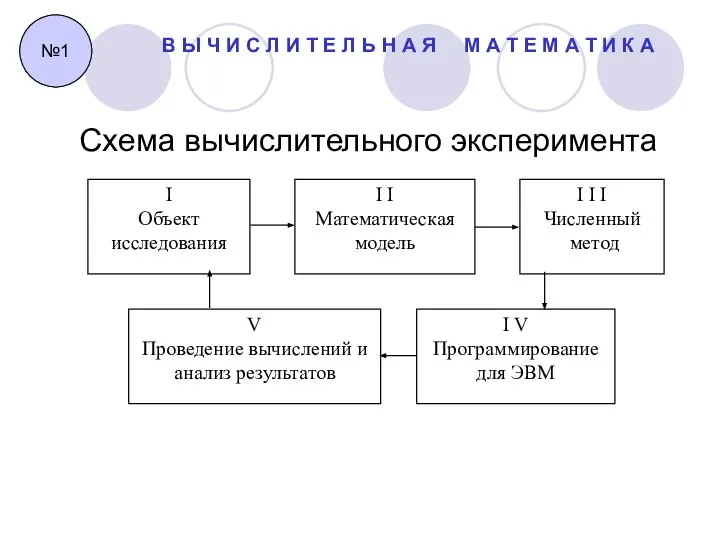
- 8. Схема вычислительного эксперимента №1 В Ы Ч И С Л И Т Е Л Ь Н
- 9. Колебание математического маятника №1 ИСТОЧНИКИ ПОГРЕШНОСТИ 1. Погрешность математической модели. Трение зависит от скорости не совсем
- 10. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 11. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 12. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 13. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
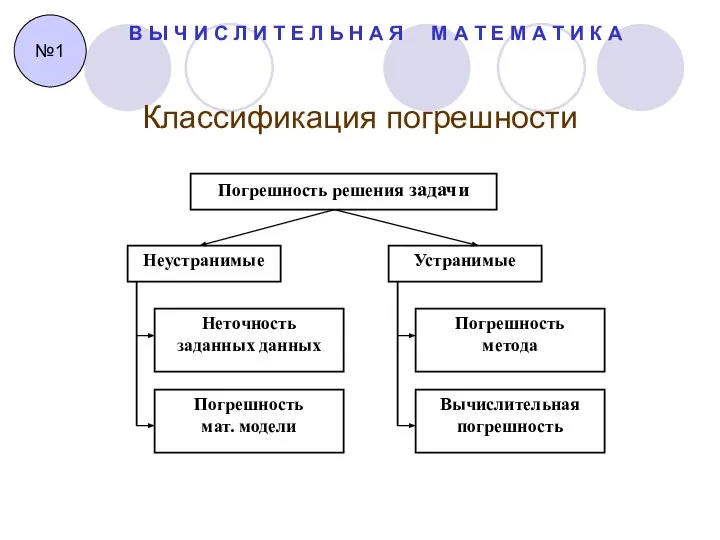
- 14. Классификация погрешности В Ы Ч И С Л И Т Е Л Ь Н А Я
- 15. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 16. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 17. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 18. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 19. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 20. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 21. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 22. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 23. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 24. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 25. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 26. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 27. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 28. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 29. ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА №1 Определение погрешности функции многих переменных по известным погрешностям аргументов абсолютную погрешность можно вычислить
- 30. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 31. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 32. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 33. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 34. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 35. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 36. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 37. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 38. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 39. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 40. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 41. В Ы Ч И С Л И Т Е Л Ь Н А Я М А
- 43. Скачать презентацию
Слайд 3В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Дополнительно:
Краевая задача 10
Контрольная работа №1 6
Контрольная работа №2 8
Контрольная работа №3 10
Критерии оценки:
5 > 93
4 > 85
3 <= 85
Слайд 4В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Список литературы
1. Киреев В.И., Пантелеев А.В. Численные методы в
примерах и задачах [Электронный ресурс]: учеб. пособие. —
СПб,; М.; Краснодар: Лань, 2015. – 448 с. [Электр. ресурс]:
ЭБС ЛАНЬ. – URL: — Режим доступа:
http://e.lanbook.com/books/element.php?pl1_id=65043 .
2. Вержбицкий В.М. Основы численных методов : Учебник
для вузов / В. М. Вержбицкий. - 2-е изд., перераб. - М. :
Высшая школа, 2005. - 847 с.
Слайд 6Специфика вычислительной математики
Вычислительная математика имеет дело не только с непрерывными, но и
Специфика вычислительной математики
Вычислительная математика имеет дело не только с непрерывными, но и

Погрешность вычислений в связи с ошибками округления;
Имеет значение обусловленность задач, т.е. чувствительность решения к малым изменениям входных данных;
Выбор вычислительного алгоритма, вообще говоря, влияет на результат вычислений;
Важная черта численного метода – экономичность, т.е. требование минимизации числа операций.
Слайд 7В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Сложные вычислительные задачи, возникающие при исследовании физических, технических и иных проблем, можно разбить на ряд элементарных — таких, как вычисление интеграла, решение дифференциального уравнения и т.п.
Посмотрим, как решается любая реальная задача, например, нахождение светового потока конструируемой лампы. Одним из способов является эксперимент. Создадим лампу и измерим интересующую нас характеристику. Если характеристика оказалась неудачной, то изменим проект, сделаем новую лампу и т.д., пока не получим желаемые параметры. Ясно, что это слишком медленный и дорогой способ. Другой способ — вычислительный эксперимент.
Слайд 9 Колебание математического маятника
№1
ИСТОЧНИКИ ПОГРЕШНОСТИ
1. Погрешность математической модели.
Трение зависит от скорости не
Колебание математического маятника
№1
ИСТОЧНИКИ ПОГРЕШНОСТИ
1. Погрешность математической модели.
Трение зависит от скорости не
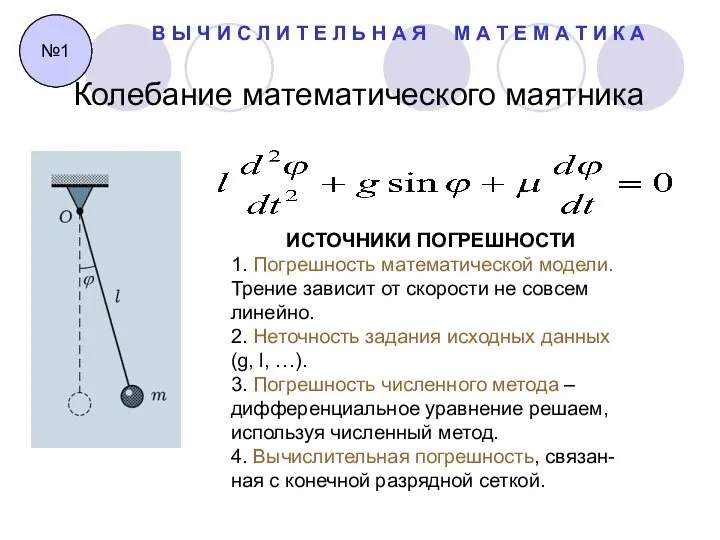
линейно.
2. Неточность задания исходных данных
(g, l, …).
3. Погрешность численного метода –
дифференциальное уравнение решаем,
используя численный метод.
4. Вычислительная погрешность, связан-
ная с конечной разрядной сеткой.
№1
В Ы Ч И С Л И Т Е Л Ь Н А Я М А Т Е М А Т И К А
№1
Слайд 10В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Иллюстрация понятия вычислительной погрешности
Вычисление синуса с помощью разложения в ряд Тейлора
Ряд сходится для любого значения x
Напишем программу для вычисления значения синуса при:
X1 = π / 6 ≈ 0.52366
X2 = 12π + π / 6 ≈ 38.22277
Слайд 11В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
#define EPS 1.e-8
#define X 0.52366
...
int i, k = 0;
double curr_sum = 0.0, curr_sum_old = 0.0, fact;
do {
fact = 1.0;
for ( i = 1; i<= 2*k+1; i++ )
fact *= i;
curr_sum_old = curr_sum;
curr_sum += pow( -1, k) * pow( X, 2*k+1 ) / fact;
k++;
} while ( fabs( curr_sum - curr_sum_old ) > EPS );
Получаем результат:
Для X1 = 0.52366: 0.500053…
Для X2 = 38.22277: 1.165079…
Слайд 12В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н
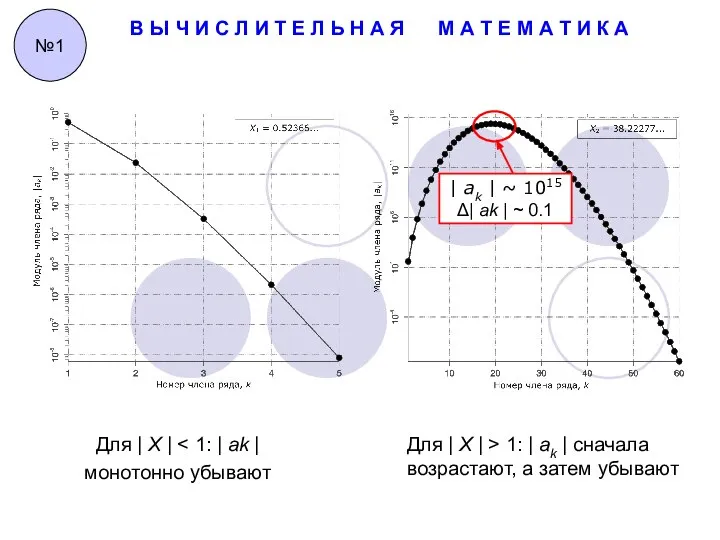
№1
| ak | ~ 1015
Δ| ak | ~ 0.1
Для | X | < 1: | ak |
монотонно убывают
Для | X | > 1: | ak | сначала возрастают, а затем убывают
Слайд 13В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Иллюстрация влияния выбора метода вычисления
Вычисление
может быть представлено как сумма сходящегося
бесконечного ряда
. Применим ряд для
При расчете с 5 знаками последовательно получим следующие числа:
Мы ограничиваемся при суммировании 25 членами ряда, так как после-дующие слагаемые уже не меняют сумму. Удовлетворительный ли ответ
получен? Истинный результат
так что вычисление
привело к ответу, не имеющему верных цифр.
Проблема таится в пятизначной арифметике и, вследствие этого, ошибках округления. Но увеличение разрядности не сильно поможет,
да и обходится очень дорого. Лучше вычислить сумму для
и затем взять обратное число:
Слайд 15В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Абсолютные и относительные погрешности
Если
— точное значение некоторой величины, а
Если
— точное значение некоторой величины, а
Если
— известное приближение к нему, то абсолютной
погрешностью приближенного значения
называют
некоторую величину
про которую известно, что
Пример:
Слайд 16В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Относительной погрешностью приближенного
значения
называют отношение его абсолютной
погрешности
к абсолютной величине числа
Пример:
Слайд 17В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Абсолютная погрешность менее информативна, чем
относительная. Так, если точное значение некоторой
Величины равно 0.00006, а приближенное значение
равно 0.00005, то абсолютная ошибка составляет всего
10-5 , в то время как относительная ошибка составляет
0.2, или 20%. С другой стороны, если точное значение
равно 100500, а приближенное значение равно 100000,
то абсолютная ошибка составляет 500, хотя относи-
тельная ошибка составляет всего 0.005, или 0.5%.
Слайд 18В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Значащими цифрами числа называются все цифры
в его записи, начиная с первой ненулевой слева. Любое
число можно представить в виде:
где
— первая значащая цифра числа;
— основание системы счисления;
Пример:
Слайд 19В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Значащая цифра
считается верной, если имеет место
неравенство:
в противном
случае
— сомнительная цифра.
В этом случае говорят, что число
имеет
верных
знаков в узком смысле.
Если
то число
имеет
верных знаков в широком
смысле.
Чаще всего
Слайд 20В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Относительная погрешность числа, содержащего
верных знаков, определяется соотношением:
На практике обычно используется понятие числа
С верными знаками в узком смысле.
Тогда можно сказать, что абсолютная погрешность числа с верными знаками равна половине последнего разряда.
Слайд 21В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Пример 1.
Приближенное число
получено с погрешностью
Определить число верных знаков в его
Согласно определению должно выполняться
неравенство
— степень первой
значащей цифры в записи числа, т.е.
тогда
цифры 0.39, а две следующие являются сомнительными.
т.е. число имеет две верные
записи.
Слайд 22В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Пример 2.
Определить абсолютную и относительную погрешность
приближенного числа
если в его
цифры :
записи только верные
Решение:
Слайд 23В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Основная задача теории погрешности заключается в следующем: по известным погрешностям некоторой системы параметров требуется определить погрешность функции этих параметров.
Определение погрешности функции по известным погрешностям аргументов
Слайд 24В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Для начала рассмотрим случай вычисления функции
одного аргумента
Абсолютная погрешность вычисления функции равна
произведению абсолютной величины ее производной
на абсолютную погрешность ее аргумента:
Слайд 25В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Рассмотрим относительную погрешность вычисления
функции одной переменной. Учитывая, что
Так как
то
можно записать так:
Слайд 26В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Относительная погрешность степени равна относительной
погрешности основания, умноженной на абсолютную
величину показателя степени.
Абсолютная погрешность равна
Для основных элементарных функций получаем
следующие правила
Степенная функция
Слайд 27В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Показательная функция
Абсолютная погрешность показательной функции равна
Относительная погрешность показательной функции равна
Для функции
получаем:
Логарифмическая функция
Абсолютная погрешность натурального логарифма числа
равна относительной погрешности самого числа:
Слайд 28В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Тригонометрические функции.
Абсолютные погрешности синуса и косинуса не
превосходят абсолютных погрешностей аргумента:
Абсолютная погрешность тангенса и котангенса всегда
больше абсолютной погрешности аргумента:
Слайд 29ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
№1
Определение погрешности функции многих переменных
по известным погрешностям аргументов
абсолютную погрешность можно вычислить
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
№1
Определение погрешности функции многих переменных
по известным погрешностям аргументов
абсолютную погрешность можно вычислить

Для непрерывно дифференцируемой функции
где
- абсолютные погрешности аргументов
Слайд 30В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Относительная погрешность вычисляется по формуле:
Учитывая, что
получим
Слайд 31В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Пример 1.
Пусть
Абсолютная погрешность суммы равна сумме абсолютных погрешностей слагаемых.
Относительная погрешность суммы:
Слайд 32В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Попробуем оценить границы относительной погрешности
суммы. Выберем из всех относительных погрешностей
наибольшую и тогда можно записать:
Таким образом, предельная относительная погрешность
суммы положительных чисел не превосходит максимальной
относительной погрешности слагаемых.
Слайд 33В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Пример 2.
Пусть
Абсолютная погрешность разности равна сумме абсолютных погрешностей аргументов.
Относительная погрешность разности:
Слайд 34В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Пример.
Пусть
Тогда
Абсолютная погрешность:
Относительная погрешность:
При вычитании близких по значению чисел относительная
погрешность может существенно возрастать…
Слайд 35В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Абсолютная и относительная погрешность вычисления
произведения и частного приближенных чисел
При умножении и делении приближенных чисел складываются их относительные погрешности, т.е. относительная погрешность выражения
оценивается величиной
Абсолютная погрешность в этом случае вычисляется
через относительную погрешность:
Слайд 36В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Определение допустимой погрешности
аргументов по допустимой погрешности функций
Эта задача имеет однозначное решение только для
функции одной переменной
: если эта функция
дифференцируема и
, то
Для функции нескольких переменных
решается только при наличии дополнительных
ограничений. Если значение одного из аргументов трудно измерить с высокой точностью других аргументов, то погрешность именно этого аргумента надо согласовать с требуемой погрешностью функции.
Слайд 37В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Если значения всех аргументов можно одинаково легко
определить с любой точностью, то обычно применяют
принцип равных влияний, считая, что в формуле
все слагаемые равны между собой;
это дает следующую формулу:
Слайд 38В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
Пример.
Найти допустимую абсолютную погрешность приближенных
величин
, для которых возможно найти
значение функции
с точностью до двух
десятичных знаков после запятой.
Решение.
Находим
Слайд 39В Ы Ч И С Л И Т Е Л Ь Н
В Ы Ч И С Л И Т Е Л Ь Н

№1
По условию
. Тогда согласно принципу равных
влияний по формуле
находим

 Площадь фигур
Площадь фигур Презентация на тему Четырёхугольники. Площади
Презентация на тему Четырёхугольники. Площади  Определённый интеграл. 11 класс
Определённый интеграл. 11 класс Урок математики в 10 В классе 8 Марта. Роль математики в повседневной жизни
Урок математики в 10 В классе 8 Марта. Роль математики в повседневной жизни Прямая призма. Решение задач
Прямая призма. Решение задач Состав числа в пределах 10. Тренажер
Состав числа в пределах 10. Тренажер Числовые и буквенные выражения
Числовые и буквенные выражения Линейная алгебра. Применение определителей
Линейная алгебра. Применение определителей Приемы вычислений для случаев вида 26+7. 2 класс
Приемы вычислений для случаев вида 26+7. 2 класс Анаграмма. Великолепная семерка
Анаграмма. Великолепная семерка Уравнения и неравенства в целых числах
Уравнения и неравенства в целых числах Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля
Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля  Алгебра логики
Алгебра логики Прямая, луч, отрезок
Прямая, луч, отрезок Базис векторного пространства
Базис векторного пространства Математическая игра
Математическая игра Вычисление неопределенных интегралов методом интегрирования по частям
Вычисление неопределенных интегралов методом интегрирования по частям Признаки параллелограмма. 8 класс
Признаки параллелограмма. 8 класс Многогранники
Многогранники Площадь трапеции
Площадь трапеции Исследование функций с помощью производных. Правила Лопиталя
Исследование функций с помощью производных. Правила Лопиталя Нормальная интерполяция
Нормальная интерполяция Математические правила и законы
Математические правила и законы Множества точек на координатной плоскости, расстояние между точками координатной прямой
Множества точек на координатной плоскости, расстояние между точками координатной прямой Занимательная геометрия (1 класс)
Занимательная геометрия (1 класс) Формирование элементарных математических представлений
Формирование элементарных математических представлений Симплексный метод
Симплексный метод Решение задач
Решение задач