Содержание
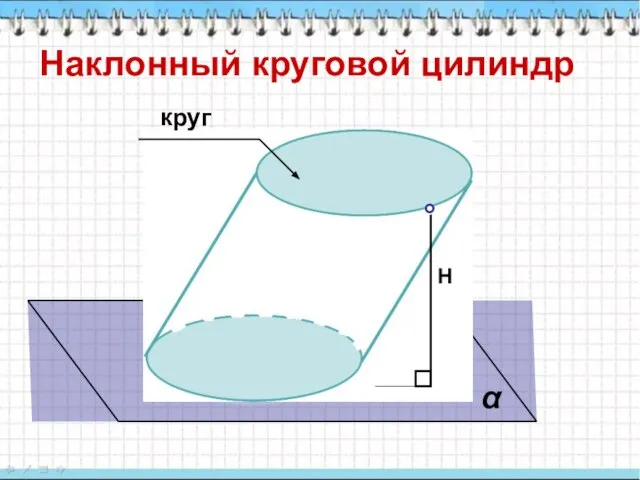
- 2. Наклонный круговой цилиндр Н круг α
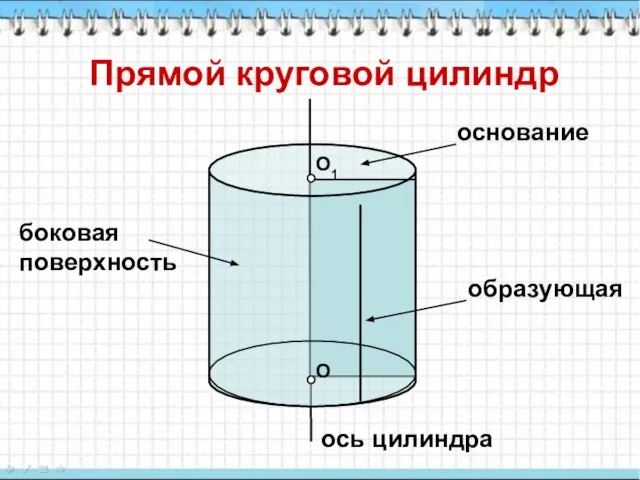
- 3. О О1 Прямой круговой цилиндр основание образующая ось цилиндра боковая поверхность
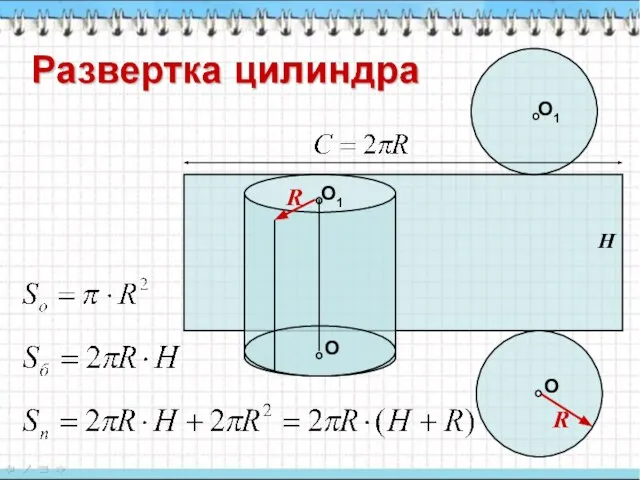
- 4. R R H
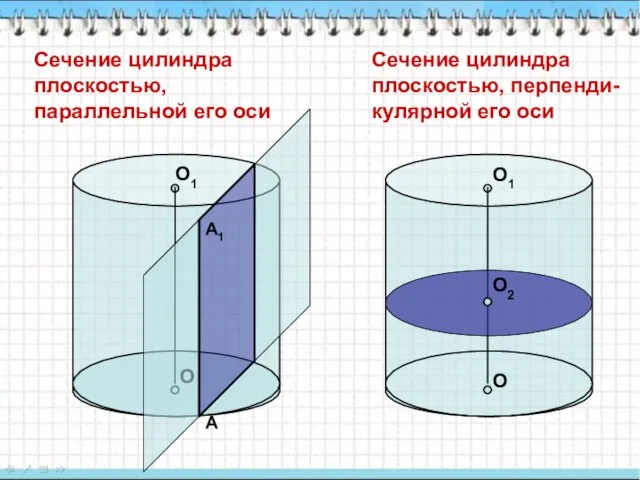
- 5. Сечение цилиндра плоскостью, параллельной его оси О О1 Сечение цилиндра плоскостью, перпенди-кулярной его оси А А1
- 8. Цилиндрическая архитектура
- 9. Найдите площадь поверхности (внешней и внутренней) шляпы, размеры которой (в см) указаны на рисунке. 1) Если
- 10. Осевое сечение цилиндра – квадрат, диагональ которого равна 20 см. Найдите: а) высоту цилиндра; б) So
- 11. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания – 5 м2. Найдите высоту цилиндра.
- 12. Концы отрезка АВ лежат на разных основаниях цилиндра. Радиус цилиндра равен r, его высота – h,
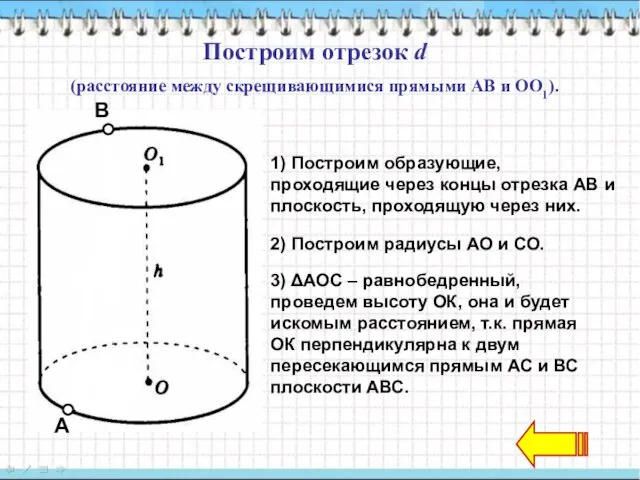
- 13. r a r d К С Построим отрезок d (расстояние между скрещивающимися прямыми АВ и ОО1).
- 14. A А1 C1 В1 Через образующую АА1 цилиндра проведены две секущие плоскости, одна из которых проходит
- 15. Плоскость γ, параллельная оси цилиндра, отсекает от окружности основания дугу AmD с градусной мерой α. Радиус
- 17. Скачать презентацию









 Решение систем неравенств. 8 класс
Решение систем неравенств. 8 класс Решение геометрических задач на нахождение площадей поверхностей и объемов многогранников
Решение геометрических задач на нахождение площадей поверхностей и объемов многогранников Отрезки. Лучи. Прямые
Отрезки. Лучи. Прямые Алгоритм Евклида
Алгоритм Евклида Тест по математике: меры времени (выражение в крупных мерах)
Тест по математике: меры времени (выражение в крупных мерах) Функции в жизни человека
Функции в жизни человека Презентация на тему Неравенства и их системы
Презентация на тему Неравенства и их системы  Правильные многогранники
Правильные многогранники Решение выражений в несколько действий
Решение выражений в несколько действий Время. Решение задач
Время. Решение задач Презентация на тему Кто хочет стать отличником
Презентация на тему Кто хочет стать отличником  Вписанная и описанная окружность. 9 класс
Вписанная и описанная окружность. 9 класс Признаки равенства треугольников
Признаки равенства треугольников Основные комбинаторные конфигурации
Основные комбинаторные конфигурации Уменьшаемое, вычитаемое, разность
Уменьшаемое, вычитаемое, разность Презентация на тему Прямоугольная система координат в пространстве (11 класс)
Презентация на тему Прямоугольная система координат в пространстве (11 класс)  Преобразования дробей
Преобразования дробей Найдите высоту и медиану треугольника
Найдите высоту и медиану треугольника Системы уравнений
Системы уравнений Мой кабинет – моя лаборатория Презентацию подготовила заведующая школьным кабинетом математики №14 Ларионова Татьяна Ивановна.
Мой кабинет – моя лаборатория Презентацию подготовила заведующая школьным кабинетом математики №14 Ларионова Татьяна Ивановна. Числа от 11 до 20. Нумерация
Числа от 11 до 20. Нумерация Тригонометрические уравнения. Устный счет
Тригонометрические уравнения. Устный счет Деление обыкновенных дробей
Деление обыкновенных дробей Решение уравнений третьей степени
Решение уравнений третьей степени Через точку А провести профильную прямую ВС, равнонаклоненную к плоскости П1 и плоскости П2. (задача 20)
Через точку А провести профильную прямую ВС, равнонаклоненную к плоскости П1 и плоскости П2. (задача 20) Функция и построение графика
Функция и построение графика Определение знаков коэффициентов K и b в линейной функции по их графикам
Определение знаков коэффициентов K и b в линейной функции по их графикам Квадратичная функция. Наглядно-методическое пособие. 9 класс
Квадратичная функция. Наглядно-методическое пособие. 9 класс