- Главная
- Математика
- Функциональная грамотность в заданиях ОГЭ

Содержание
- 2. Хранение и передача знаний, навыков, норм и идеалов, образцов деятельности и поведения, социальных ценностей и ориентаций
- 3. Под математической функциональной грамотностью следует подразумевать способность личности использовать приобретенные математические знания для решения задач в
- 4. Для формирования коммуникативной компетентности можно использовать групповую форму организации познавательной деятельности учащихся на уроках. Учащимся можно
- 5. Для формирования исследовательской компетентности учащимся можно предложить задания, в которых необходимо исследовать все возможные варианты и
- 6. Готовность к разрешению проблем формируется с помощью задач, в которых необходимо проанализировать предложенную ситуацию, поставить цель,
- 7. Формирование определенной системы математических знаний всегда было в центре внимания в математическом образовании. Объем этой системы
- 8. Функциональная грамотность становится фактором, содействующим развитию способностей школьников творчески мыслить и находить стандартные решения, умений выбирать
- 10. Скачать презентацию
Слайд 2Хранение и передача знаний, навыков, норм и идеалов, образцов деятельности и поведения,

Функциональная грамотность – «способность человека решать стандартные жизненные задачи в различных сферах жизни и деятельности на основе прикладных знаний».
Функционально грамотная личность – это человек, ориентирующийся в мире и действующий в соответствии с общественными ценностями, ожиданиями и интересами.
Основные признаки функционально грамотной личности: это человек самостоятельный, познающий и умеющий жить среди людей, обладающий определёнными качествами, ключевыми компетенциями.
Слайд 3
Под математической функциональной грамотностью следует подразумевать способность личности использовать приобретенные математические знания для решения задач
Под математической функциональной грамотностью следует подразумевать способность личности использовать приобретенные математические знания для решения задач

На уроках математики дети учатся:
• выполнять математические расчеты для решения повседневных задач; • рассуждать, делать выводы на основе информации, представленной в различных формах (в таблицах, диаграммах, на графиках), широко используемых в средствах массовой информации.
Образование является особой формой мышления, которая, подчиняясь диалектическим законам, поэтапно проводит обучающегося от незнания – к знанию, от владения знаниями – к их применению, а затем – к созданию новых знаний.
Именно поэтому, задания, призванные исследовать состояние математической грамотности учеников, имеют четко выраженную прикладную направленность и их решение предусматривает владение учащимися приемами деятельности прикладного характера.
Слайд 4Для формирования коммуникативной компетентности можно использовать групповую форму организации познавательной деятельности учащихся на уроках. Учащимся можно
Для формирования коммуникативной компетентности можно использовать групповую форму организации познавательной деятельности учащихся на уроках. Учащимся можно

№5 На плане (см. рисунок) изображена местность, прилегающая к озеру Круглому. Для удобства план нанесён на квадратную сетку, сторона каждого квадрата которой равна 500 м. Населённые пункты обозначены на плане жирными точками.
Рядом с озером Круглое находится болото, обозначенное на плане штриховкой. На болоте расположен хутор Камышино. От хутора Камышино проложена дорога к деревне Дубки, вокруг которой имеются дубовые рощи. Далее дорога идёт к селу Большое, расположенному по другую сторону озера от хутора Камышино. Село Большое соединено также дорогой с деревней Малая, обозначенной на плане цифрой 7. Деревня Малая, в свою очередь, соединена дорогой с деревней Дальней (отмечена цифрой 4). Преобладающая часть изображённой на плане местности — это поля, используемые для выращивания злаков.
РЕШЕНИЕ
Сторона одной клетки равна 500 м. Значит, 2 км дороги из хутора Камышино в деревню Дальняя будет проходить по болоту, а 0,5 км — по полю. Следовательно, стоимость дороги из хутора Камышино в деревню Дальняя равна
2*20+0,5*10=45 млн рублей.
Далее, 1 км дороги из хутора Камышино в деревню Малая будет проходить по болоту, а другие 3 км — по полю. Следовательно, стоимость дороги из хутора Камышино в деревню Малая равна
1*20+3*10=50млн рублей.
Таким образом, стоимость дороги из хутора Камышино в деревню Дальняя меньше и равна 45 млн рублей.
Ответ: 45.
Слайд 5Для формирования исследовательской компетентности учащимся можно предложить задания, в которых необходимо исследовать все возможные
Для формирования исследовательской компетентности учащимся можно предложить задания, в которых необходимо исследовать все возможные
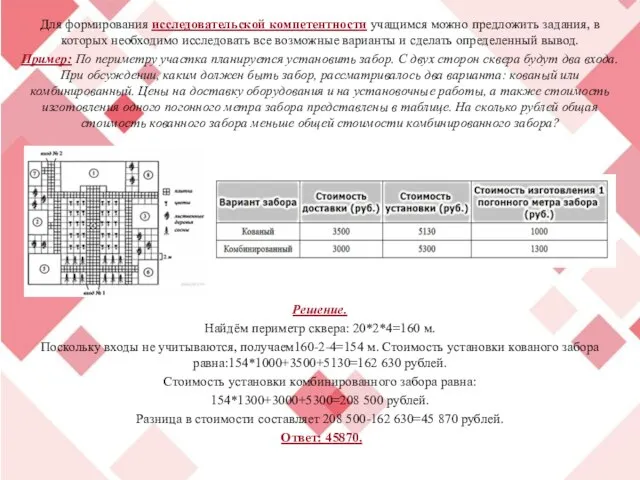
Пример: По периметру участка планируется установить забор. С двух сторон сквера будут два входа. При обсуждении, каким должен быть забор, рассматривалось два варианта: кованый или комбинированный. Цены на доставку оборудования и на установочные работы, а также стоимость изготовления одного погонного метра забора представлены в таблице. На сколько рублей общая стоимость кованного забора меньше общей стоимости комбинированного забора?
Решение.
Найдём периметр сквера: 20*2*4=160 м.
Поскольку входы не учитываются, получаем160-2-4=154 м. Стоимость установки кованого забора равна:154*1000+3500+5130=162 630 рублей.
Стоимость установки комбинированного забора равна:
154*1300+3000+5300=208 500 рублей.
Разница в стоимости составляет 208 500-162 630=45 870 рублей.
Ответ: 45870.
Слайд 6Готовность к разрешению проблем формируется с помощью задач, в которых необходимо проанализировать предложенную
Готовность к разрешению проблем формируется с помощью задач, в которых необходимо проанализировать предложенную
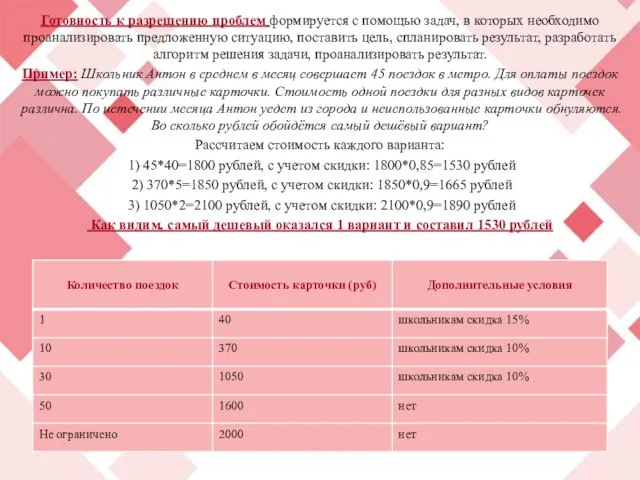
Пример: Школьник Антон в среднем в месяц совершает 45 поездок в метро. Для оплаты поездок можно покупать различные карточки. Стоимость одной поездки для разных видов карточек различна. По истечении месяца Антон уедет из города и неиспользованные карточки обнуляются. Во сколько рублей обойдётся самый дешёвый вариант?
Рассчитаем стоимость каждого варианта:
1) 45*40=1800 рублей, с учетом скидки: 1800*0,85=1530 рублей
2) 370*5=1850 рублей, с учетом скидки: 1850*0,9=1665 рублей
3) 1050*2=2100 рублей, с учетом скидки: 2100*0,9=1890 рублей
Как видим, самый дешевый оказался 1 вариант и составил 1530 рублей
Слайд 7Формирование определенной системы математических знаний всегда было в центре внимания в математическом
Формирование определенной системы математических знаний всегда было в центре внимания в математическом

Успешное выполнение контекстных заданий может быть обеспечено только при ориентации учебного процесса на решение подобных задач.
Чтобы повысить математическую грамотность учащихся, можно предложить учащимся самим составить задачи и уравнения, ребусы, кроссоворды, разноуровневые задания.
В связи с этим давайте все запомним одну математическую формулу, которая позволит сформировать у учащихся в процессе изучения математики и других дисциплин качества мышления, необходимые для полноценного функционирования человека в современном обществе.
«ОВЛАДЕНИЕ = УСВОЕНИЕ + ПРИМЕНЕНИЕ ЗНАНИЙ НА ПРАКТИКЕ»
Слайд 8Функциональная грамотность становится фактором, содействующим развитию способностей школьников творчески мыслить и находить
Функциональная грамотность становится фактором, содействующим развитию способностей школьников творчески мыслить и находить

Таким образом, задачи по формированию функциональной грамотности, в частности, математической грамотности обучающихся, возможно реализовать при условии оптимального сочетания учебного содержания базового уровня образования и дополнительных курсов, направленных на совершенствование прикладных математических умений, использующихся в различных жизненных ситуациях.
 Вписанная окружность
Вписанная окружность Брейн-ринг
Брейн-ринг Презентация на тему Использование здоровьесберегающих технологий на уроках математики
Презентация на тему Использование здоровьесберегающих технологий на уроках математики  МатШах(0.1)
МатШах(0.1)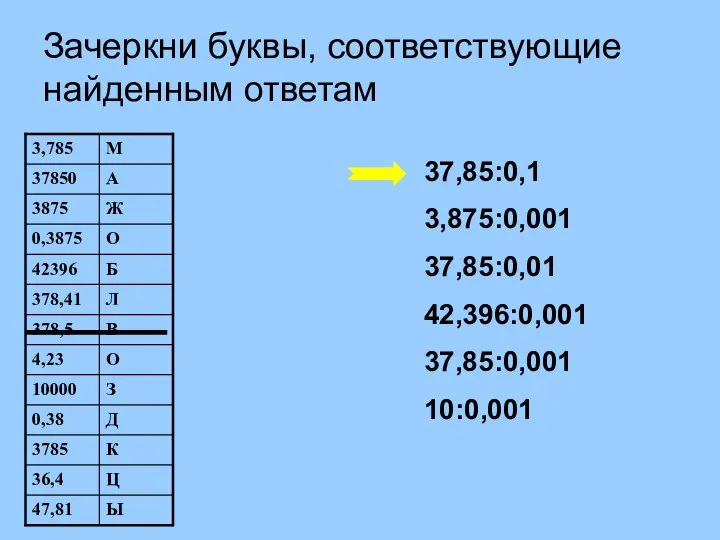 Устная работа (1). Зачеркни буквы, соответствующие найденным ответам
Устная работа (1). Зачеркни буквы, соответствующие найденным ответам Логарифмические уравнения и неравенства. Практическая работа
Логарифмические уравнения и неравенства. Практическая работа Повторение по математике
Повторение по математике Понятие вектора
Понятие вектора Занимательные задачи
Занимательные задачи Вычислить. Задание на лето
Вычислить. Задание на лето Оформление заданий по математике согласно федеральным образовательным стандартам Программа школа 2100
Оформление заданий по математике согласно федеральным образовательным стандартам Программа школа 2100 Свойство углов при основании равнобедренного треугольника
Свойство углов при основании равнобедренного треугольника Прямоугольный треугольник
Прямоугольный треугольник Звёздчатые многогранники
Звёздчатые многогранники Вычисление площади фигур на клетчатой бумаге
Вычисление площади фигур на клетчатой бумаге Вариационный ряд. Группировка данных при качественной и количественной вариациях
Вариационный ряд. Группировка данных при качественной и количественной вариациях Призма. Площадь поверхности призмы. 10 класс
Призма. Площадь поверхности призмы. 10 класс Расстояния в пространстве
Расстояния в пространстве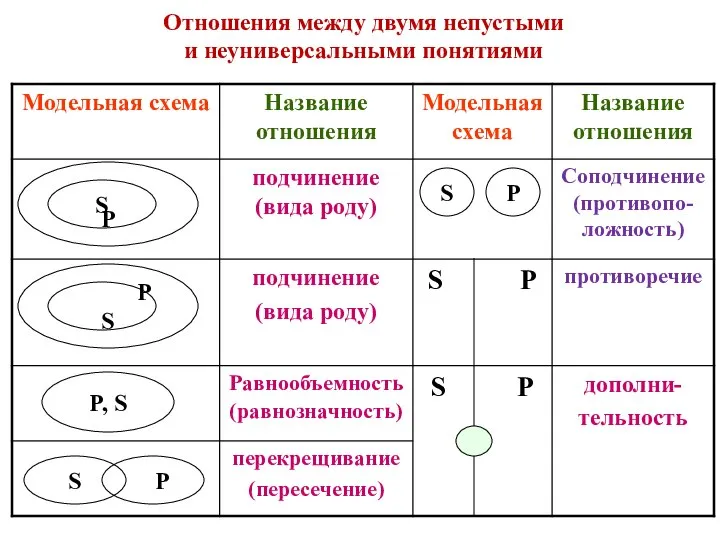 Отношения между двумя непустыми и неуниверсальными понятиями. Модельная схема
Отношения между двумя непустыми и неуниверсальными понятиями. Модельная схема Презентация на тему График функции (7 класс)
Презентация на тему График функции (7 класс)  В мире многогранников
В мире многогранников Нормальная интерполяция
Нормальная интерполяция Графики функций. Задачи с параметрами
Графики функций. Задачи с параметрами Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Решение системы линейных уравнений. Методы решения системы линейных уравнений
Решение системы линейных уравнений. Методы решения системы линейных уравнений Метрическая система мер
Метрическая система мер Перпендикулярность плоскостей
Перпендикулярность плоскостей Уравнения и неравенства с одной переменной
Уравнения и неравенства с одной переменной