Показательная функция. Показательные уравнения

Определение
Показательная функция – это функция вида ,
где x – переменная,
- заданное число, >0, ≠1.
Примеры:

Свойства показательной функции
Область определения:
все действительные числа
Множество значений:
все положительные числа
При > 1 функция возрастающая;
при 0 < < 1 функция убывающая.
D(y) = R;
E(y) = (0; + ∞);

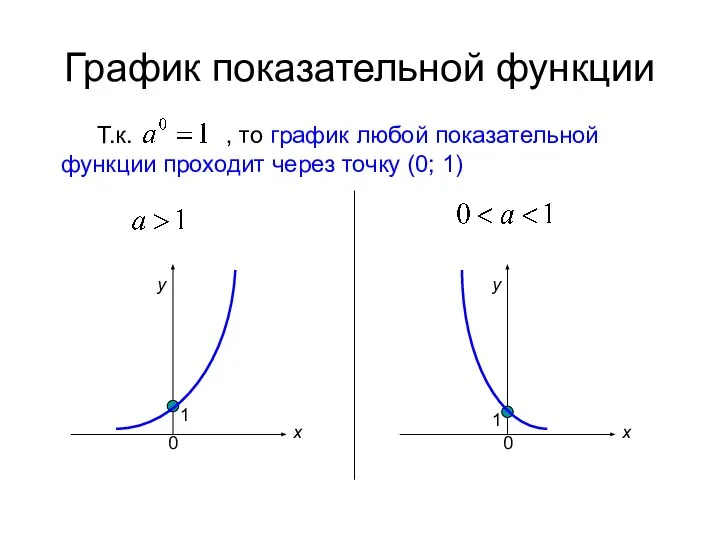
График показательной функции
Т.к. , то график любой показательной функции проходит через точку (0; 1)
1
1
х
х
у
у
0
0

Показательные уравнения
Определение
Простейшие уравнения
Способы решения сложных уравнений

Определение
Уравнение, в котором переменная содержится в показателе степени, называется показательным.
Примеры:

Простейшее показательное уравнение – это уравнение вида
Простейшее показательное уравнение решается с использованием свойств степени.

Способы решения сложных показательных уравнений.
Вынесение за скобки степени с меньшим показателем
Замена переменной
Деление на показательную функцию

Вынесение за скобки степени с меньшим показателем
Данный способ используется, если соблюдаются два условия:
1) основания степеней
одинаковы;
2) коэффициенты перед
переменной одинаковы
Например:

Замена переменной
При данном способе показательное уравнение сводится к квадратному.
Способ замены переменной используют, если
показатель одной из степеней в 2 раза больше, чем
у другой.
Например:
3 2x – 4 · 3 х – 45 = 0
коэффициенты перед
переменной противоположны.
Например:
2 2 - х – 2 х – 1 =1
б)
а) основания степеней одинаковы;

Деление на показательную функцию
Данный способ используется, если основания степеней разные.
а) в уравнении вида ax = bx делим на bx
Например: 2х = 5х | : 5x
б) в уравнении A a2x + B (ab)x + C b2x = 0
делим на b2x.
Например:
3⋅25х - 8⋅15х + 5⋅9х = 0 | : 9x

Показательные неравенства
Определение
Простейшие неравенства
Решение неравенств

Определение
Показательные неравенства –
это неравенства, в которых неизвестное содержится в показателе степени.
Примеры:

Простейшие показательные неравенства – это неравенства вида:
где a > 0, a ≠ 1, b – любое число.

При решении простейших неравенств используют свойства возрастания или убывания показательной функции. Для решения более сложных показательных неравенств используются те же способы, что и при решении показательных уравнений.

Показательная функция
Построение графика
Сравнение чисел с использованием свойств показательной функции
Сравнение числа с 1
а) аналитический способ;
б) графический способ.

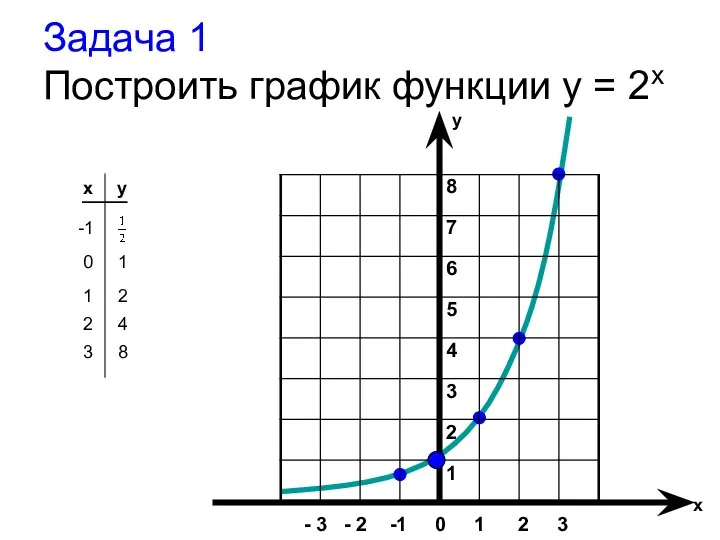
Задача 1
Построить график функции y = 2x
x
y
-1
8
7
6
5
4
3
2
1
- 3 - 2 -1 0 1 2 3
х
у
3 8
2 4
1 2
0 1

Задача 2
Сравнить числа
Решение
Ответ:

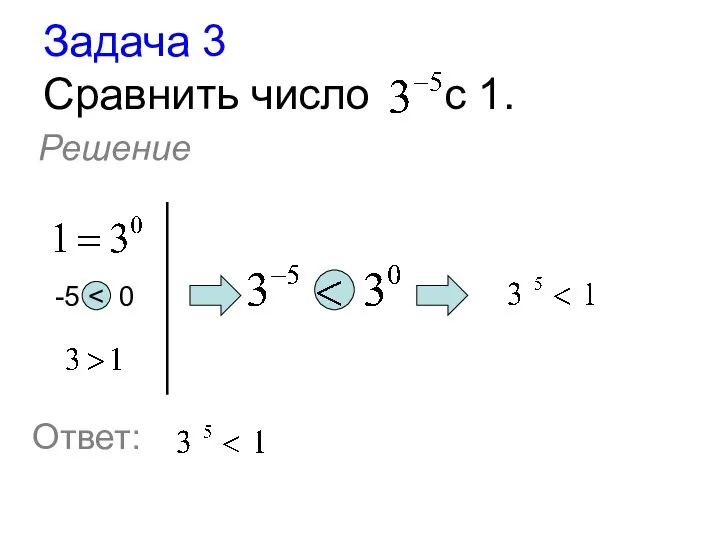
Задача 3
Сравнить число с 1.
Решение
-5 < 0
Ответ:

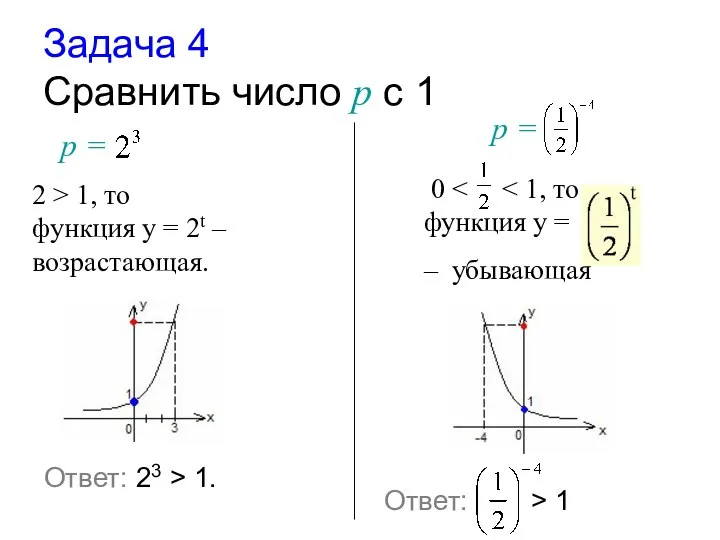
Задача 4
Cравнить число р с 1
р =
2 > 1, то функция у = 2t – возрастающая.
0 < < 1, то
функция у =
– убывающая
Ответ: 23 > 1.
Ответ:
> 1
р =

Решение показательных уравнений
Простейшие показательные уравнения
Уравнения, решаемые вынесением за скобки степени с меньшим показателем
Уравнения, решаемые заменой переменной
случай 1;
случай 2.
Уравнения, решаемые делением на показательную функцию
случай 1;
случай 2.

Простейшие показательные уравнения
Ответ: - 5,5.
Ответ: 0; 3.

Вынесение за скобки степени с меньшим показателем
Ответ: 5
x + 1 - (x - 2) =
= x + 1 – x + 2 = 3

Замена переменной (1)
основания степеней одинаковы, показатель одной из степеней в 2 раза больше, чем у другой .
3 2x – 4 · 3 х – 45 = 0
t = 3x (t > 0)
t 2 – 4t – 45 = 0
По т. Виета: t1· t 2 = - 45; t1+ t 2 =4
t1 = 9; t 2 = - 5 – не удовлетворяет условию
3x = 9; 3x = 32; x = 2.
Ответ: 2

Замена переменной (2)
Основания степеней одинаковы,
коэффициенты перед переменной противоположны.
По т. Виета:
- Не удовлетворяет условию
Ответ: 1

Деление
на показательную функцию
Ответ: 0