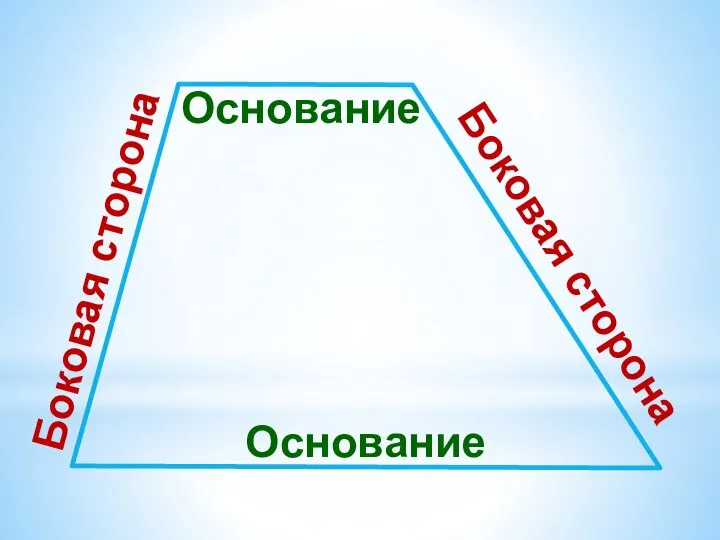
Слайд 2Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны

не параллельны
(Трапе́ция от др.-греч. τραπέζιον— «столик» от τράπεζα— «стол»)
Слайд 4Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции
M – середина
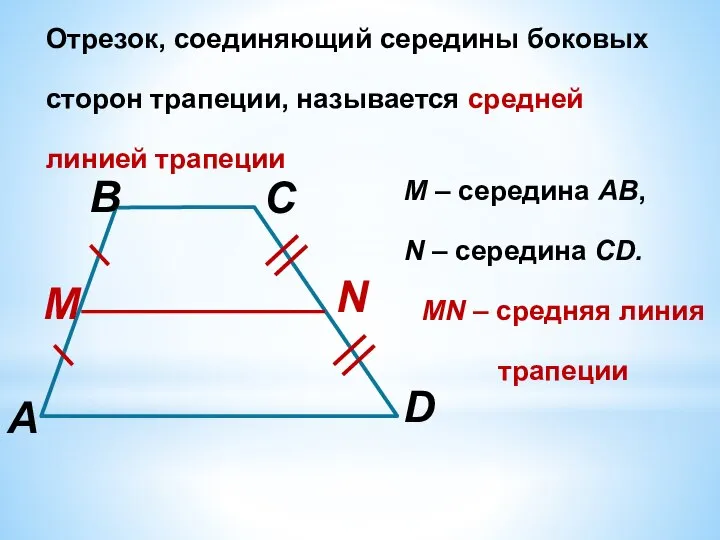
АВ,
N – середина CD.
MN – средняя линия трапеции
Слайд 5Трапеция называется равнобедренной, если её боковые стороны равны
Виды трапеций
Трапеция, один из углов
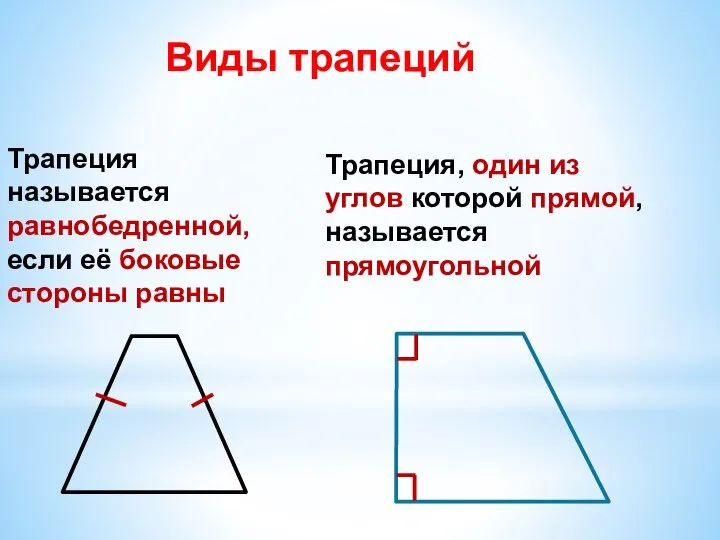
которой прямой, называется прямоугольной
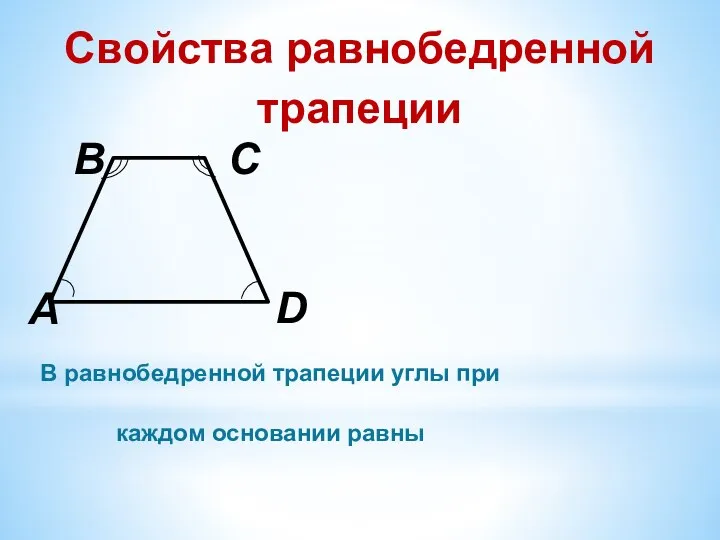
Слайд 6Свойства равнобедренной трапеции
В равнобедренной трапеции углы при каждом основании равны
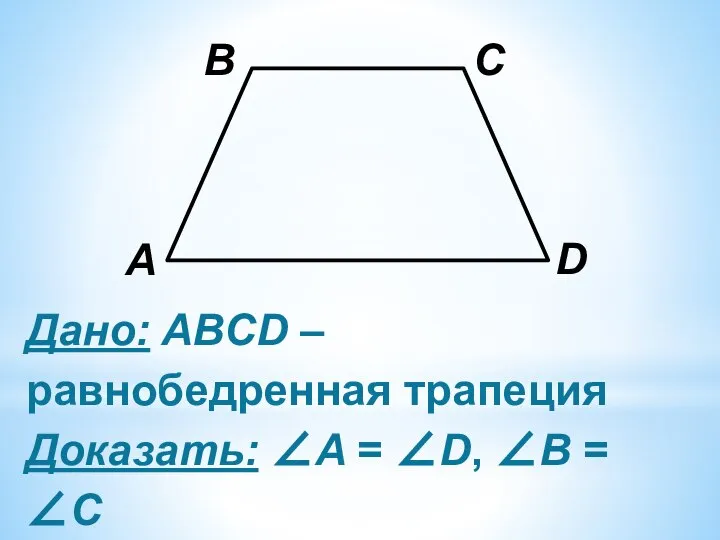
Слайд 7Дано: ABCD – равнобедренная трапеция Доказать: ∠A = ∠D, ∠B = ∠C
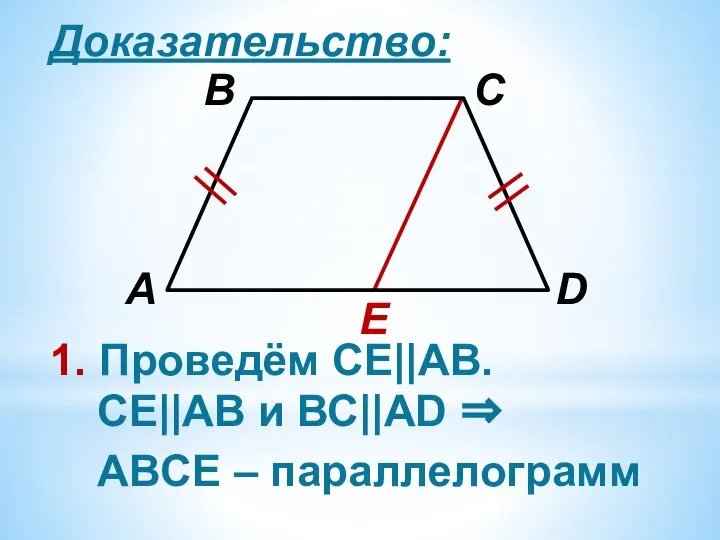
Слайд 8Доказательство:
E
1. Проведём СЕ||АВ.
СЕ||АВ и ВС||АD ⇒
ABCЕ – параллелограмм
Слайд 9Доказательство:
E
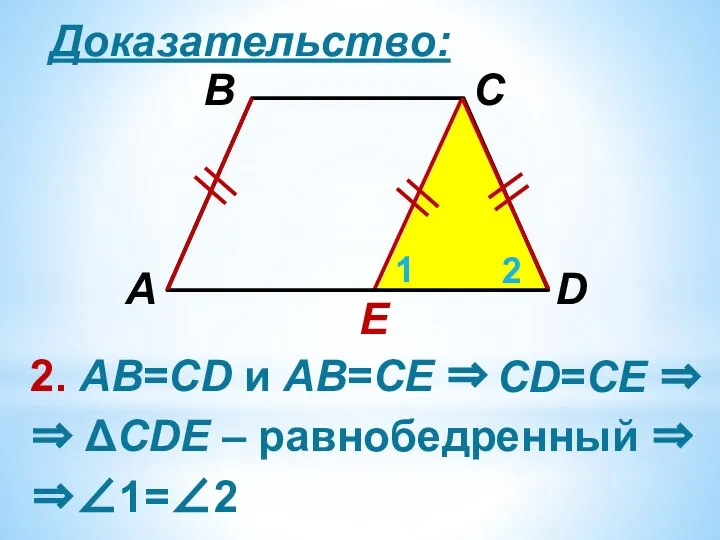
2. АВ=CD и АВ=СЕ ⇒
1
2
⇒ ΔCDЕ – равнобедренный ⇒
CD=СЕ ⇒
⇒∠1=∠2
Слайд 10Доказательство:
E
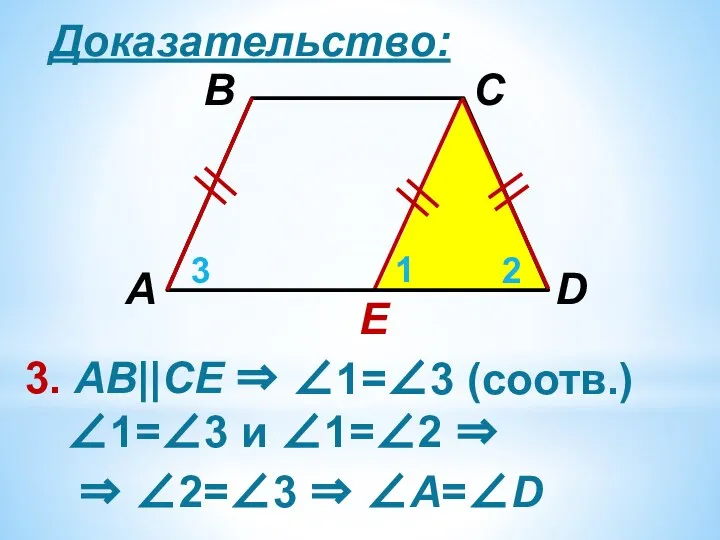
3. АВ||CЕ ⇒
1
2
3
∠1=∠3 (соотв.)
∠1=∠3 и ∠1=∠2 ⇒
⇒ ∠2=∠3 ⇒ ∠А=∠D
Слайд 11Доказательство:
E
4. ∠АВC = 1800 – ∠А
1
2
3
∠ВCD = 1800 – ∠D
∠А=∠D
∠АВC =
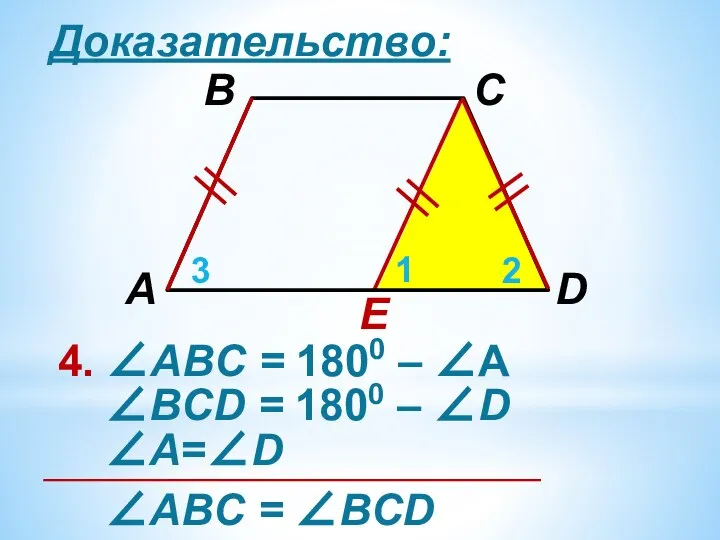
∠ВCD
Слайд 12В равнобедренной трапеции диагонали равны
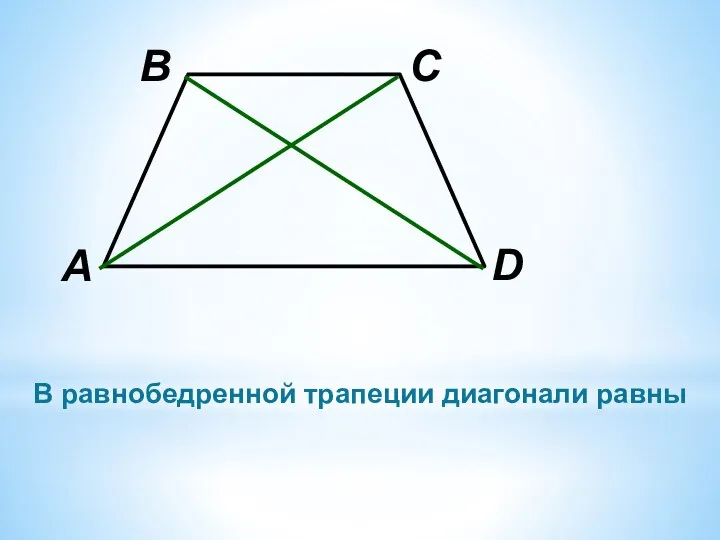
Слайд 13Дано: ABCD – равнобедренная трапеция Доказать: АС = ВD
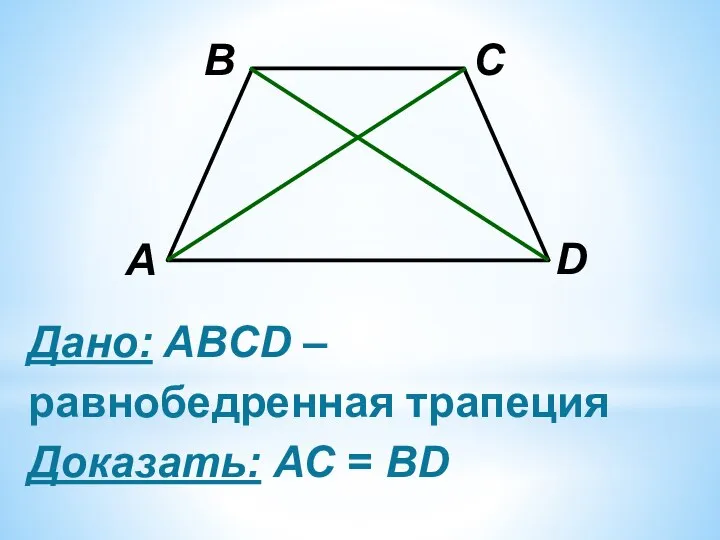
Слайд 14Доказательство:
1. Рассм. ΔАВС и ΔВCD
АB=CD – по опр. равноб. трап.
∠АВС =∠BCD
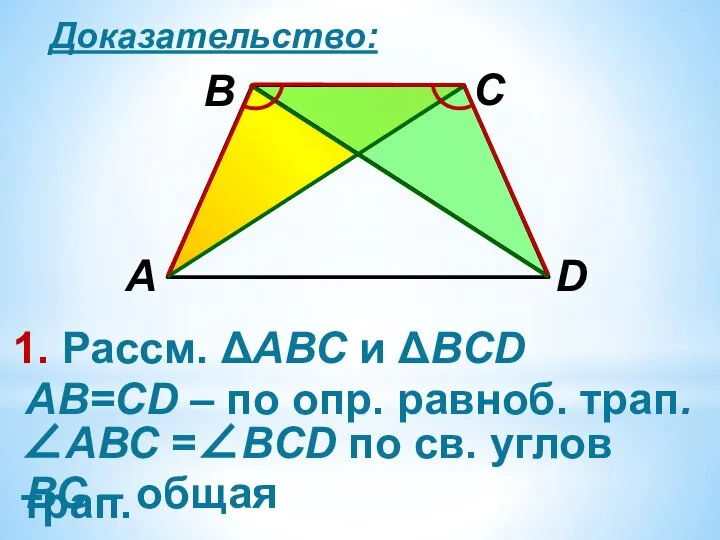
по св. углов трап.
ВС – общая
Слайд 15Доказательство:
2. ΔАВС = ΔВCD по 2 сторонам и углу между ними ⇒
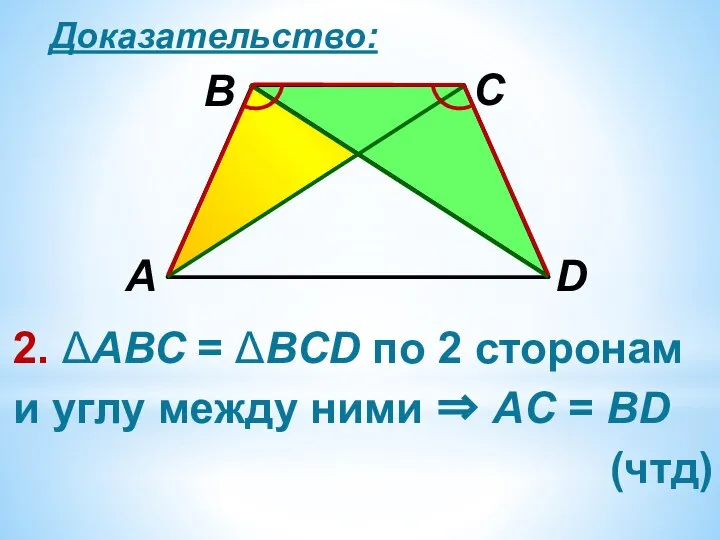
АC = BD
(чтд)
Слайд 16Свойства равнобедренной трапеции
В равнобедренной трапеции углы при каждом основании равны
В равнобедренной трапеции

диагонали равны
Слайд 17Признаки равнобедренной трапеции
Если углы при каждом основании трапеции равны, то она равнобедренная
Если

диагонали трапеции равны, то она равнобедренная















 Обобщающий урок по теме: параллелограм, прямоугольник, ромб, квадрат
Обобщающий урок по теме: параллелограм, прямоугольник, ромб, квадрат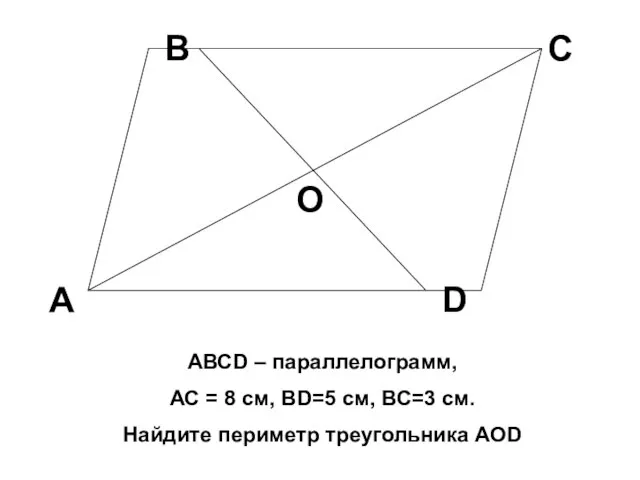 АВСD – параллелограмм
АВСD – параллелограмм Вопросы собеседования по математике для лиц, поступающих на базе среднего профессионального образования
Вопросы собеседования по математике для лиц, поступающих на базе среднего профессионального образования Операции с вероятностями по электроснабжению (задачи)
Операции с вероятностями по электроснабжению (задачи) Производная сложной функции
Производная сложной функции Задание 19. Профиль (1)
Задание 19. Профиль (1) Математический словарь
Математический словарь Арктангенс числа
Арктангенс числа Великолепная семёрка. Игра-викторина
Великолепная семёрка. Игра-викторина Углы между прямыми и плоскостями (координатный метод), 11 класс
Углы между прямыми и плоскостями (координатный метод), 11 класс Аттестационная работа. Взаимодействие учебной и исследовательской деятельности на уроках математики
Аттестационная работа. Взаимодействие учебной и исследовательской деятельности на уроках математики Математика в медицине. Области применения
Математика в медицине. Области применения Математическая прогрессия и где её применяют
Математическая прогрессия и где её применяют Изучение геометрического материала по программе Л.Г. Петерсон Школа 2000
Изучение геометрического материала по программе Л.Г. Петерсон Школа 2000 Шар и сфера
Шар и сфера Тригонометрические функции
Тригонометрические функции Контрольная работа. Логарифм, логарифмическая функция
Контрольная работа. Логарифм, логарифмическая функция Показательные и логарифмические уравнения, системы, неравенства
Показательные и логарифмические уравнения, системы, неравенства Геометрическая задача на вычисление
Геометрическая задача на вычисление вычитание векторов 13.10
вычитание векторов 13.10 Квадратные уравнения
Квадратные уравнения Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Таблица значений синуса, косинуса, тангенса для углов
Таблица значений синуса, косинуса, тангенса для углов Применение производной для нахождения наибольших и наименьших значений величин
Применение производной для нахождения наибольших и наименьших значений величин Уравнения и неравенства. Решение квадратных неравенств с помощью метода интервалов
Уравнения и неравенства. Решение квадратных неравенств с помощью метода интервалов Diskretnaya_matematika-2 2
Diskretnaya_matematika-2 2 Организация исследовательской деятельности учащихся на уроках математики
Организация исследовательской деятельности учащихся на уроках математики Решение задач. Математика 3 класс
Решение задач. Математика 3 класс