Содержание
- 2. Повторение Матрицей называется квадратная.
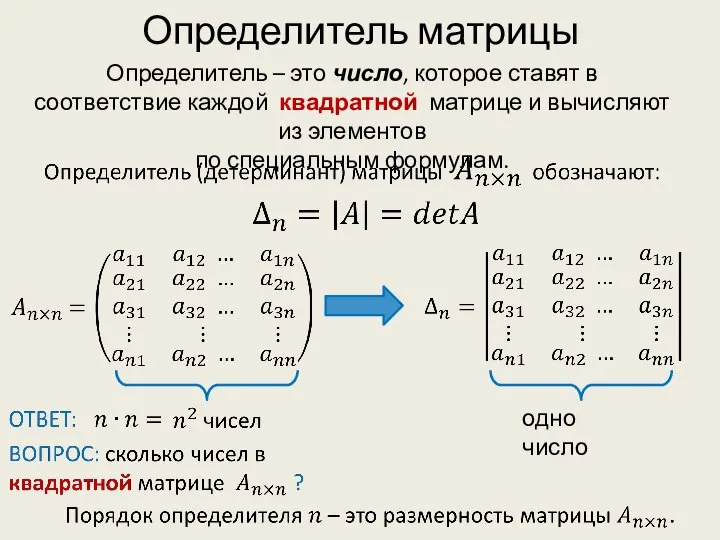
- 3. Определитель матрицы Определитель – это число, которое ставят в соответствие каждой квадратной матрице и вычисляют из
- 4. Определитель второго порядка – это разность произведений элементов, стоящих на главной диагонали и на побочной диагонали:
- 5. Примеры вычисления определителей второго порядка ОСНОВНОЕ ТРИГОНОМЕТРИЧЕСКОЕ ТОЖДЕСТВО Пример 1. Пример 2. ОТВЕТ ОТВЕТ Пример 3.
- 6. Для запоминания этой формулы используют Для умножения выбираем по ТРИ элемента составим ШЕСТЬ наборов по ТРИ
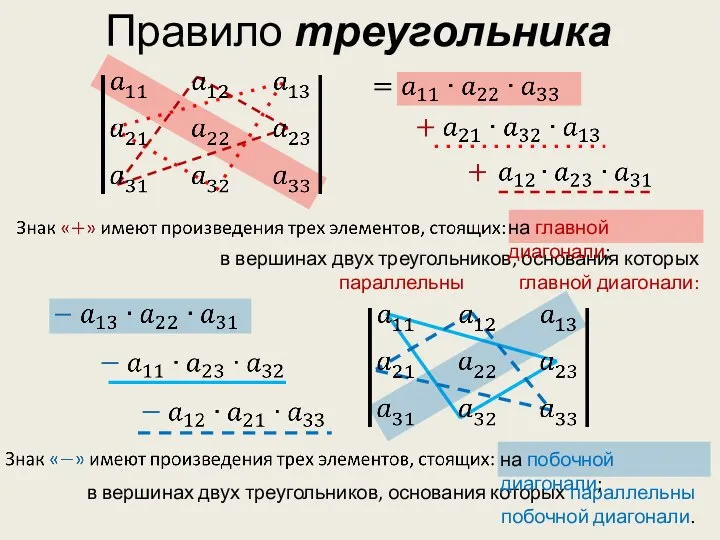
- 7. Правило треугольника в вершинах двух треугольников, основания которых параллельны главной диагонали: на главной диагонали; в вершинах
- 8. Правило Саррюса Припишем справа к определителю первый и второй столбец.
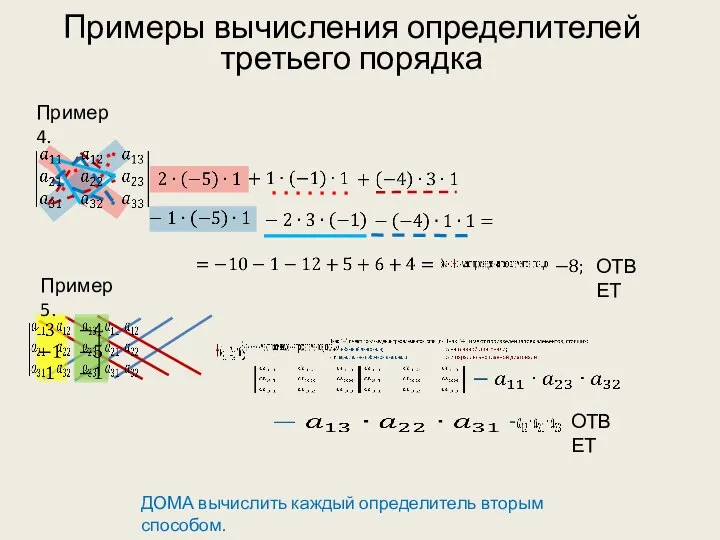
- 9. ОТВЕТ Примеры вычисления определителей третьего порядка Пример 4. ДОМА вычислить каждый определитель вторым способом. Пример 5.
- 10. Решение систем уравнений с помощью определителей(правило Крамера) Пусть задана система из двух уравнений с двумя неизвестными:
- 11. Составим новый определитель: Составим еще один определитель: то система не имеет решений.
- 12. Примеры решения системы из двух уравнений Вычислим определители: Как проверить ответ? Пример 6. ОТВЕТ: Составим матрицы
- 13. Решение системы из трёх уравнений Определитель системы Поставим столбец правых частей вместо первого столбца определителя системы.
- 14. то система не имеет решений. , то решение системы находим по формулам Крамера: , то система
- 16. Скачать презентацию










 Умножение числа 3 на однозначные числа
Умножение числа 3 на однозначные числа Задачи на части
Задачи на части Задачи на готовых чертежах. Ромб
Задачи на готовых чертежах. Ромб Применение признаков подобия треугольников к решению задач и доказательству теорем
Применение признаков подобия треугольников к решению задач и доказательству теорем Координаты вектора
Координаты вектора Применение производной в физике
Применение производной в физике Роль и место математики в современном мире. Пределы, их свойства (лекция 1)
Роль и место математики в современном мире. Пределы, их свойства (лекция 1) Оценка сложных систем в условиях неопределенности
Оценка сложных систем в условиях неопределенности Навыки решения составных задач
Навыки решения составных задач Преемственность в формировании УПК младших школьников и учащихся 5-6 классов на уроках математики посредством интеграции
Преемственность в формировании УПК младших школьников и учащихся 5-6 классов на уроках математики посредством интеграции Координаты и вектора
Координаты и вектора Час занимательной математики
Час занимательной математики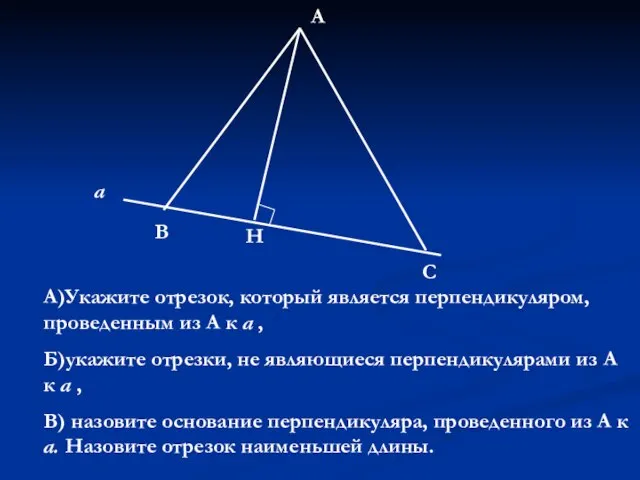 Построение треугольника
Построение треугольника Презентация на тему Усеченный конус
Презентация на тему Усеченный конус  Устный счёт для дошкольников
Устный счёт для дошкольников Системы линейных уравнений
Системы линейных уравнений Решение логарифмических уравнений к занятию
Решение логарифмических уравнений к занятию Презентация на тему РЕШЕНИЕ ЗАДАЧ НА НАХОЖДЕНИЕ ПЛОЩАДИ ПОВЕРХНОСТИ И ОБЪЕМОВ ТЕЛ ВРАЩЕНИЯ
Презентация на тему РЕШЕНИЕ ЗАДАЧ НА НАХОЖДЕНИЕ ПЛОЩАДИ ПОВЕРХНОСТИ И ОБЪЕМОВ ТЕЛ ВРАЩЕНИЯ  Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ
Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ  Презентация на тему РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Презентация на тему РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ  Турнір з математики
Турнір з математики Свойства предметов (часть 2)
Свойства предметов (часть 2) Функции у=|x| и ей график
Функции у=|x| и ей график Правило двух решений. Подход Неймана-Пирсона
Правило двух решений. Подход Неймана-Пирсона Принципы статистического оценивания. Анализ данных
Принципы статистического оценивания. Анализ данных Решение задач по теме Арифметическая прогрессия
Решение задач по теме Арифметическая прогрессия Условия с логическими связками. Задачи
Условия с логическими связками. Задачи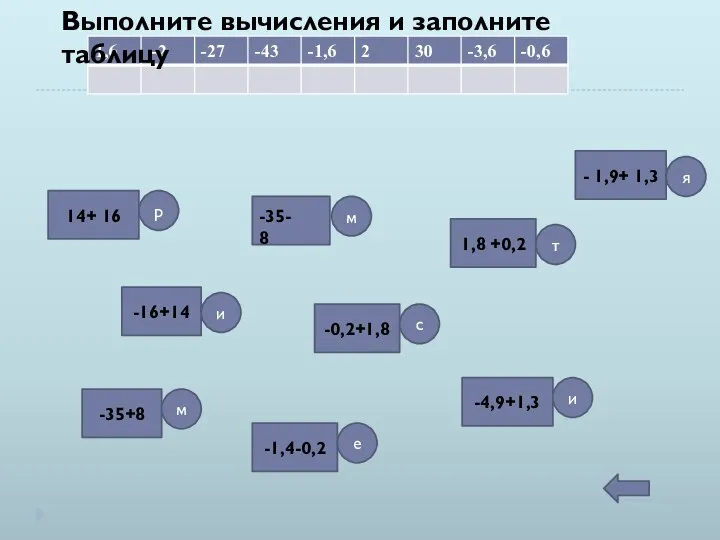 Выполните вычисления и заполните таблицу. 6 класс
Выполните вычисления и заполните таблицу. 6 класс