Слайд 2Мета лекції
Отримання знань щодо алгебри логіки

Слайд 3Питання, що будуть розглянуті
Логічні (булеві) функції.
Алгебра логіки.
Повні набори функцій
Канонічні форми

булевих функцій.
Спрощення формул. Утворення скороченої ДНФ методом Квайна
Слайд 5Вступ до алгебри логіки
Порівняння основних властивостей множин та логіки висловлювань показало, що

ці властивості мають багато спільного.
Як результат з’явилась Булева алгебра, яка є частиною математичної логіки.
Слайд 6Вступ до алгебри логіки
Математична логіка є сучасний вид формальної логіки, науки, що

вивчає умовиводи з точки зору їхнього формального створення.
Основи математичної логіки закладено в таких працях англійського математика Джорджа Буля (1815 – 1864) як «Математичний аналіз логіки» (1847) і «Закони мислення» (1854), де він уперше виклав алгебру логіки – алгебру Буля.
Слайд 7Логічні (булеві) змінні
Означення 1.1. Логічними (булевими) змінними в булевій алгебрі називають величини,

які незалежно від їхньої конкретної суті можуть набувати лише двох значень.
Слайд 8Логічні (булеві) змінні
Ці значення будемо позначати нулем (0) й одиницею (1), маючи

на увазі, що 0 і 1 це формальні символи, що не мають арифметичного змісту, а зображують будь-які змінні, що набувають лише двох значень, наприклад „ТАК” і „НІ”, „ІСТИННО” (І) – „ХИБНО” (Х) і т.д.
Якщо змінна має одиничне значення, то записуємо x=1, а якщо нульове, то x=0.
Слайд 10Сфери застосування булевих функцій
В обчислювальній техніці булеві функції застосовуються для:
опису алгоритмів,
засобів

цієї техніки – дискретних пристроїв, які призначаються для перетворення дискретної інформації, що розкладається на елементарні одиниці – біти, які в пристроях реалізуються сигналами, що описуються двійковими змінними – булевими.
Для вирішення деяких економічних задач
Для вирішення задач цілочисельного програмування
Слайд 17Основні способи подання булевих функцій

Слайд 23Область визначення логічної функції

Слайд 24Область визначення логічної функції. Приклад

Слайд 26Елементарні функції алгебри логіки

Слайд 27Елементарні функції алгебри логіки

Слайд 35Поняття формули в алгебрі логіки

Слайд 36Поняття формули в алгебрі логіки

Слайд 37Приклади формул в алгебрі логіки

Слайд 38Приклади формул в алгебрі логіки

Слайд 39Зв’язок між функцією та формулою в алгебрі логіки

Слайд 40Зв’язок між функцією та формулою в алгебрі логіки

Слайд 41Зв’язок між функцією та формулою в алгебрі логіки. Приклад

Слайд 48Універсальність функції стрілки
Пірса-Вебба

Слайд 49Універсальність функції стрілки
Пірса-Вебба

Слайд 50Універсальність функції стрілки
Пірса-Вебба

Слайд 574. Канонічні форми булевих функцій

Слайд 59Тотожно хибна та здійсненна формули

Слайд 67Диз’юнктивна нормальна форма. Приклад

Слайд 68Диз’юнктивна нормальна форма. Приклад

Слайд 70Досконала диз’юнктивна нормальна форма

Слайд 71Досконала диз’юнктивна нормальна форма

Слайд 72Досконала диз’юнктивна нормальна форма. Приклад

Слайд 73Спосіб «розгортання» ДНФ до вигляду ДДНФ деякої функції, що залежить від n

змінних
Слайд 74Ще один спосіб «розгортання», виходячи з табличного представлення

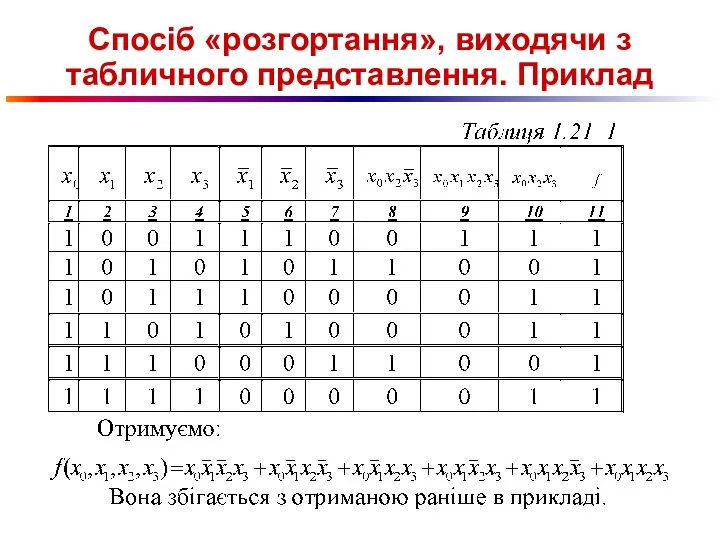
Слайд 75Спосіб «розгортання», виходячи з табличного представлення. Приклад
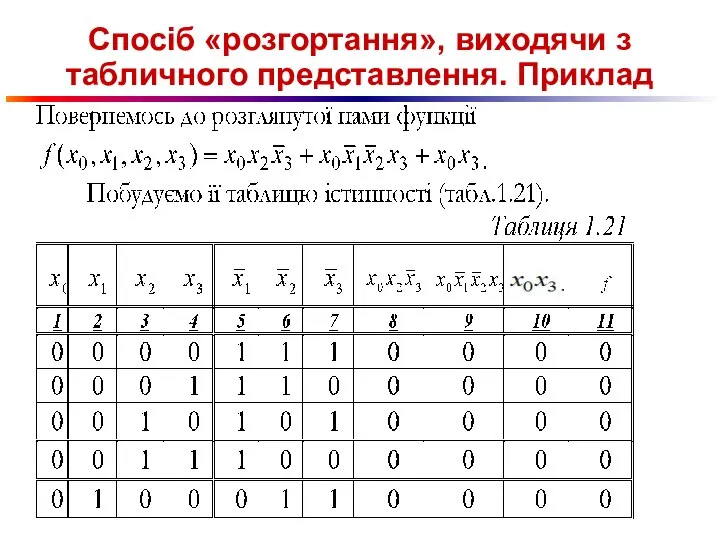
Слайд 76Спосіб «розгортання», виходячи з табличного представлення. Приклад
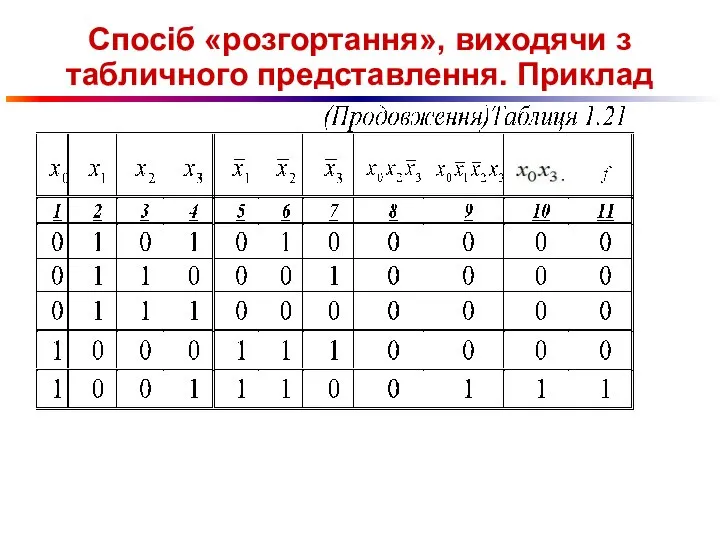
Слайд 77Спосіб «розгортання», виходячи з табличного представлення. Приклад
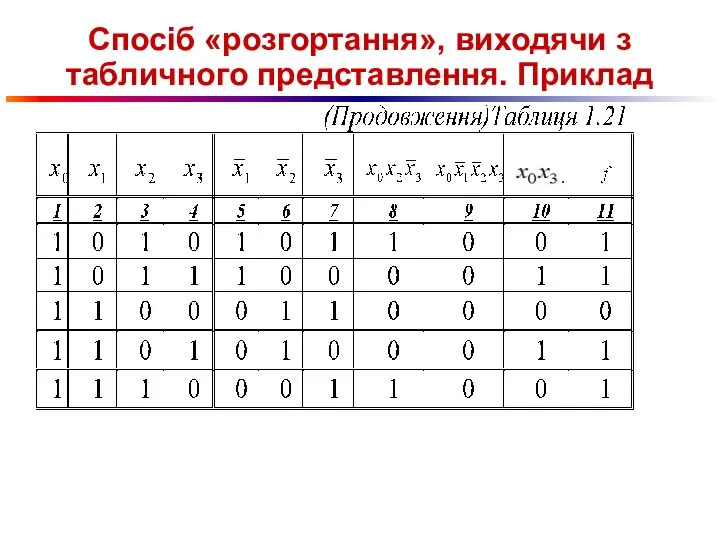
Слайд 78Спосіб «розгортання», виходячи з табличного представлення. Приклад
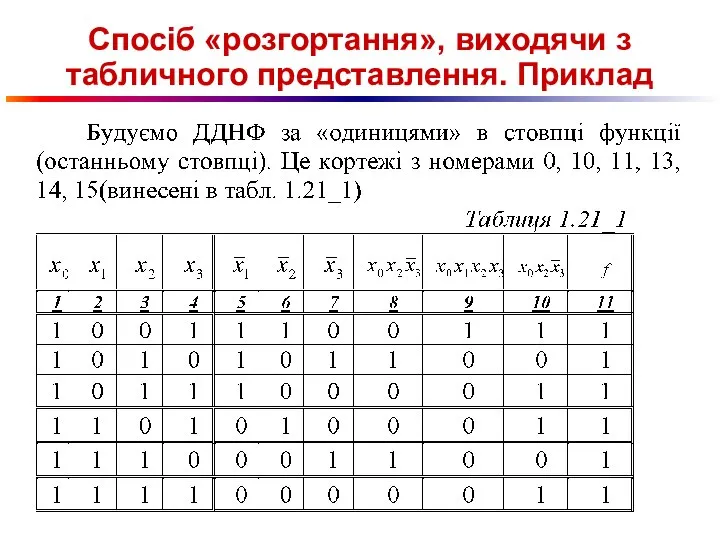
Слайд 79Спосіб «розгортання», виходячи з табличного представлення. Приклад
Слайд 82Довершена кон’юктивна нормальна форма

Слайд 83Довершена кон’юктивна нормальна форма

Слайд 84Спосіб «розгортання» КНФ деякої функції до вигляду ДКНФ

Слайд 85Спосіб «розгортання» КНФ деякої функції до вигляду ДКНФ. Приклад

Слайд 86Спосіб «розгортання» за табличним поданням функції

Слайд 87Спосіб «розгортання» за табличним поданням функції. Приклад
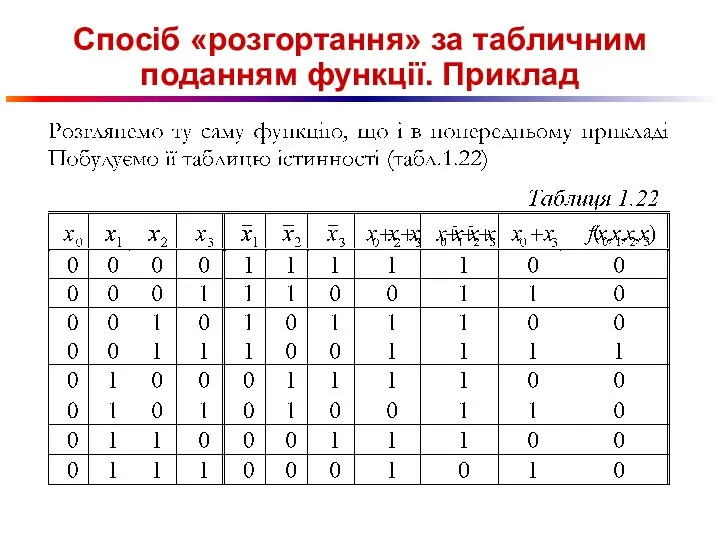
Слайд 88Спосіб «розгортання» за табличним поданням функції. Приклад
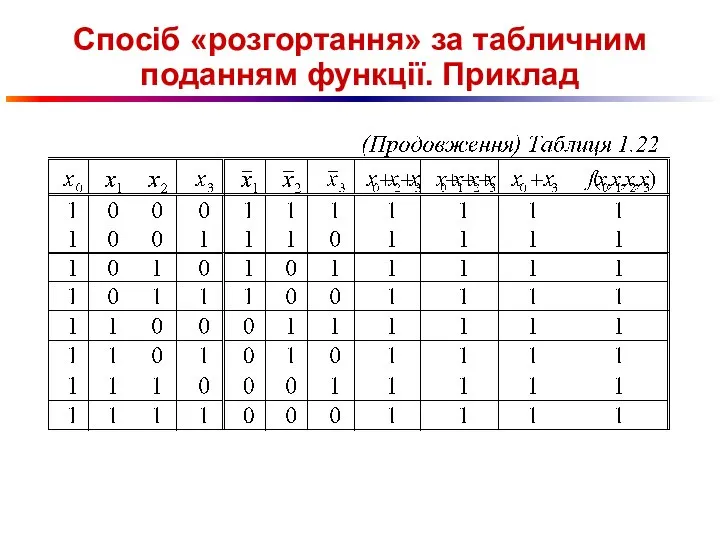
Слайд 89Спосіб «розгортання» за табличним поданням функції. Приклад
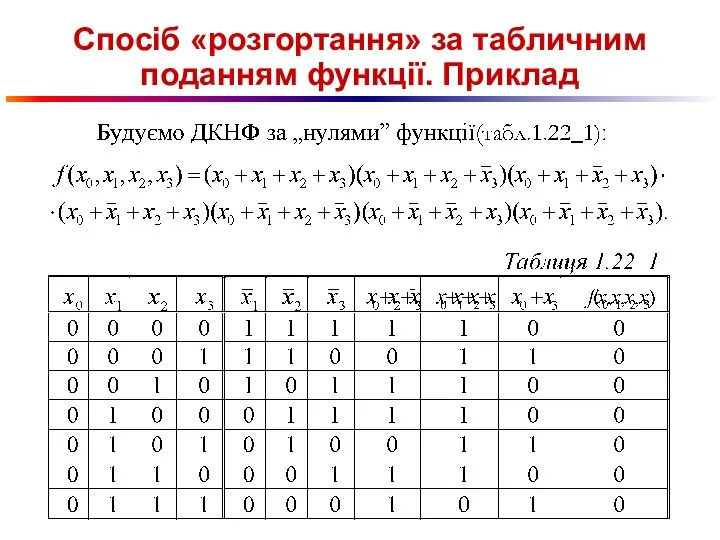
Слайд 92Утворення скороченої ДНФ методом Квайна

Слайд 93Операції повного склеювання та поглинання

Слайд 95Метод Квайна. 1 етап. Початкове скорочення формули.

Слайд 96Метод Квайна. 1 етап. Початкове скорочення формули.Приклад

Слайд 97Метод Квайна. 1 етап. Початкове скорочення формули.Приклад
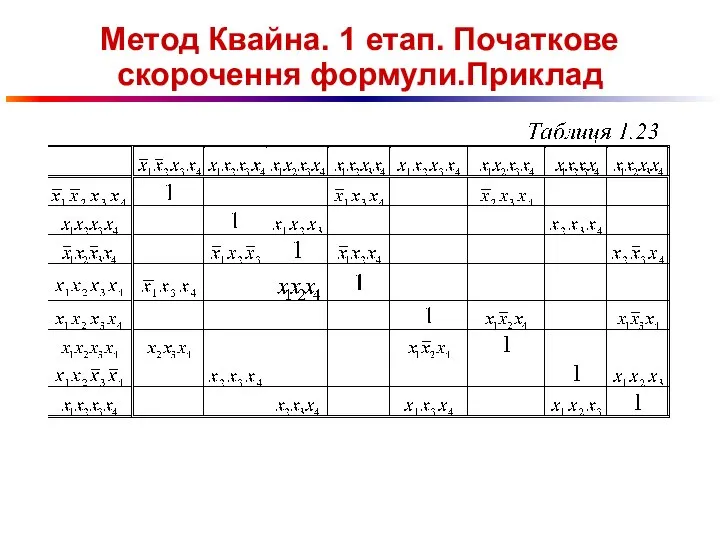
Слайд 98Метод Квайна. 1 етап. Початкове скорочення формули.Приклад

Слайд 99Метод Квайна. 1 етап. Початкове скорочення формули.Приклад

Слайд 100Метод Квайна. 1 етап. Початкове скорочення формули.Приклад
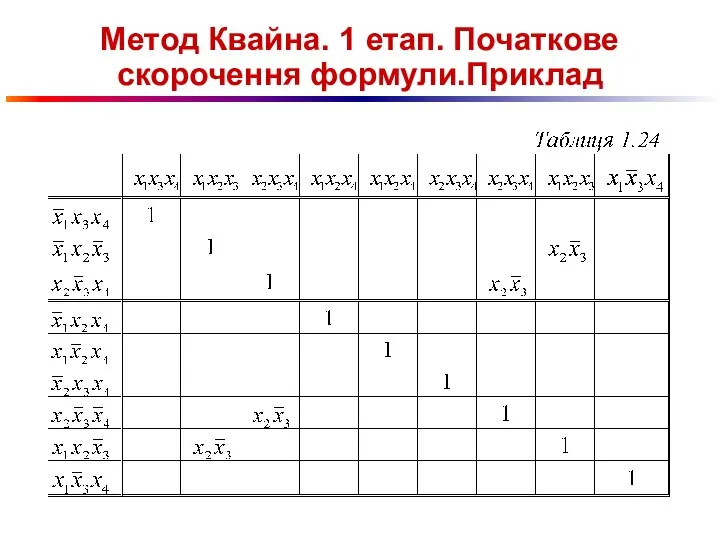
Слайд 101Метод Квайна. 1 етап. Початкове скорочення формули.Приклад

Слайд 102Метод Квайна. 2 етап. Розставляння міток.

Слайд 103Метод Квайна. 2 етап. Розставляння міток. Приклад

Слайд 104Метод Квайна. 3 етап. Знаходження суттєвих доданків.

Слайд 105Метод Квайна. 3 етап. Знаходження суттєвих доданків.

Слайд 106Метод Квайна. 3 етап. Розставляння міток. Приклад

Слайд 107Метод Квайна. 4 етап. Викреслювання зайвих стовпців.

Слайд 108Метод Квайна. 5 етап. Викреслювання зайвих кон’юнкцій скороченої ДНФ.

Слайд 109Метод Квайна. 6 етап. Вибір мінімального покриття.

Слайд 110Метод Квайна. 6 етап. Вибір мінімального покриття. Приклад

Слайд 111Питання, що були розглянуті
Логічні (булеві) функції.
Алгебра логіки.
Повні набори функцій
Канонічні форми

булевих функцій.
Спрощення формул. Утворення скороченої ДНФ методом Квайна












































































































 Поверхности и тела. Проецирование геометрических фигур
Поверхности и тела. Проецирование геометрических фигур Решение простейших логарифмических неравенств
Решение простейших логарифмических неравенств Векторная алгебра. Скалярное, векторное и смешанное произведения векторов. Лекция 2
Векторная алгебра. Скалярное, векторное и смешанное произведения векторов. Лекция 2 Вектор. Равенство векторов. Откладывание вектора равного данному
Вектор. Равенство векторов. Откладывание вектора равного данному Презентация на тему Отношения и пропорции
Презентация на тему Отношения и пропорции  Перпендикуляр и наклонная к плоскости. Решение задач
Перпендикуляр и наклонная к плоскости. Решение задач Презентация на тему Статистика и математика
Презентация на тему Статистика и математика  Презентация на тему Цилиндры и цилиндрические поверхности (11 класс)
Презентация на тему Цилиндры и цилиндрические поверхности (11 класс)  Аксиома параллельных прямых
Аксиома параллельных прямых Работа с графиками функций
Работа с графиками функций Составление фигур из спичек
Составление фигур из спичек Признаки равенства треугольников
Признаки равенства треугольников Математика в кинематографии
Математика в кинематографии Погрешности измерительных приборов. Класс точности
Погрешности измерительных приборов. Класс точности Периметр восьмиугольника
Периметр восьмиугольника Базіс лінейнай прасторы. Каардынаты
Базіс лінейнай прасторы. Каардынаты Решение треугольников
Решение треугольников Симметрия относительно точки
Симметрия относительно точки Логика. Задания
Логика. Задания Презентация на тему Вычисления с многозначными числами
Презентация на тему Вычисления с многозначными числами  Неравенства. Решить систему неравенств
Неравенства. Решить систему неравенств Презентация на тему Биссектриса угла в треугольнике
Презентация на тему Биссектриса угла в треугольнике  Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3
Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3 История происхождения математических знаков
История происхождения математических знаков Открой свою звезду. Математический диктант
Открой свою звезду. Математический диктант ЕГЭ математика — профильный уровень. Задание 9
ЕГЭ математика — профильный уровень. Задание 9 Дифуры 1 порядка
Дифуры 1 порядка Матрицы
Матрицы