Содержание
- 2. План урока. Тема: Призма. Построение сечений призмы плоскостями. Цель: Дать определение призмы. Научить строить сечения призмы
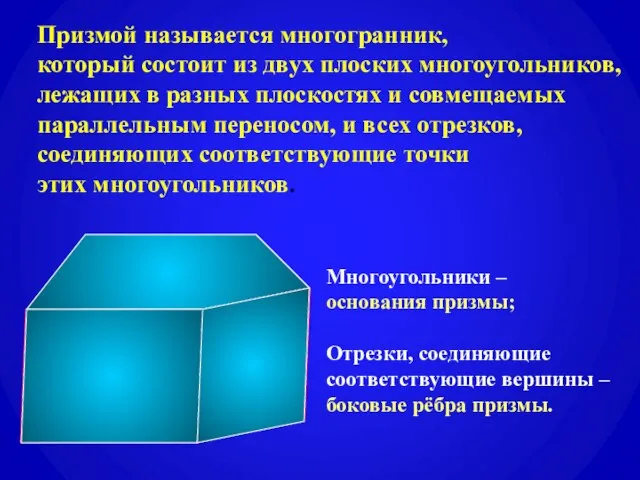
- 3. Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным
- 4. Различные виды призм.
- 5. Построение сечений призмы. Сечения призмы плоскостями, проходящими через два боковых ребра, не принадлежащих одной грани.
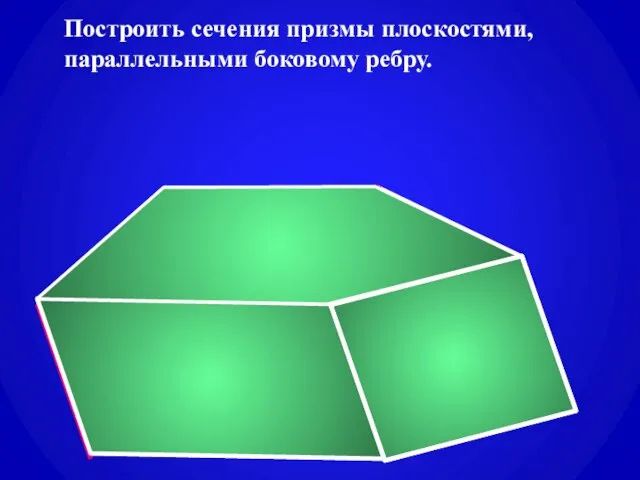
- 6. Построить сечения призмы плоскостями, параллельными боковому ребру.
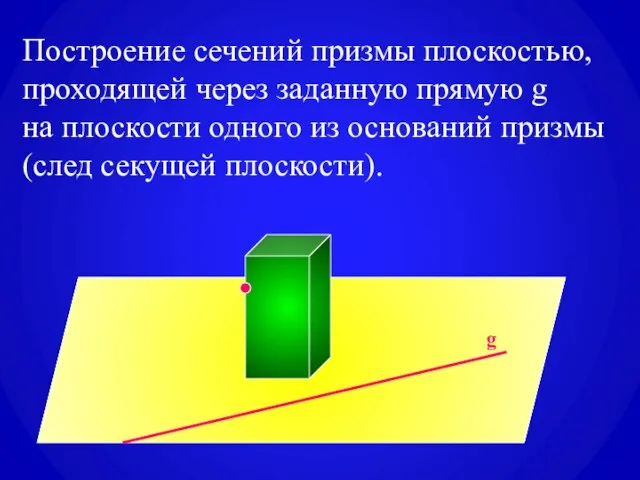
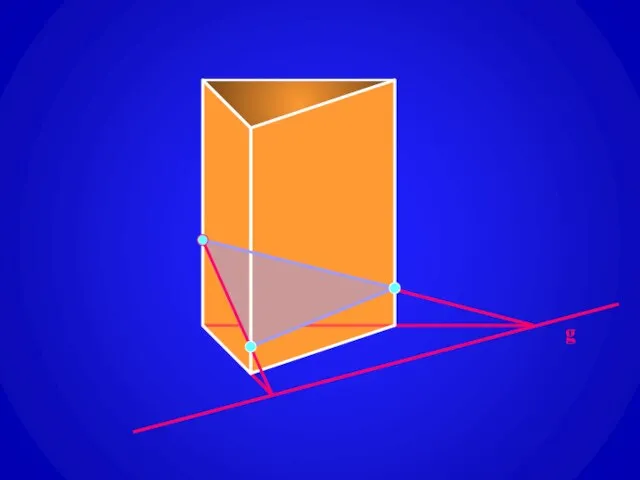
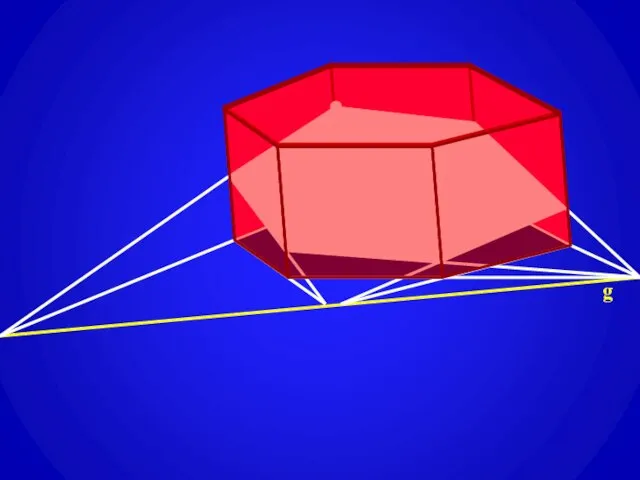
- 7. Построение сечений призмы плоскостью, проходящей через заданную прямую g на плоскости одного из оснований призмы (след
- 8. g
- 9. g
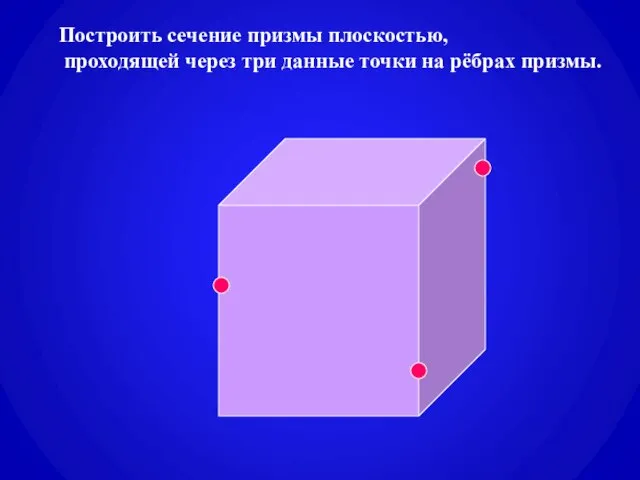
- 10. Построить сечение призмы плоскостью, проходящей через три данные точки на рёбрах призмы.
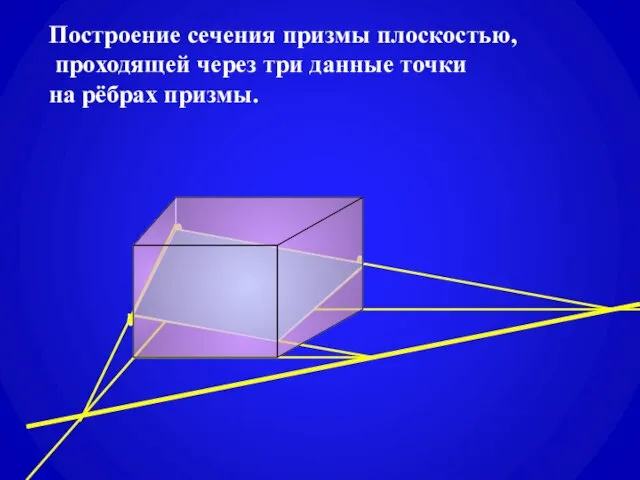
- 11. Построение сечения призмы плоскостью, проходящей через три данные точки на рёбрах призмы.
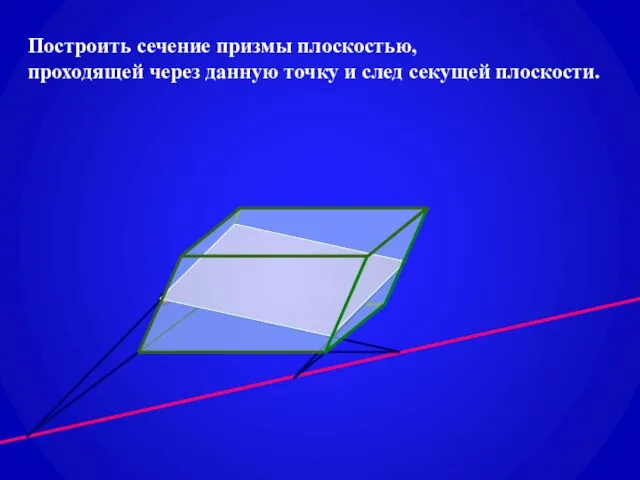
- 12. Построить сечение призмы плоскостью, проходящей через данную точку и след секущей плоскости.
- 14. Скачать презентацию



 Найди фигуру (развиваем логику)
Найди фигуру (развиваем логику) Графики тригонометрических функций. 10 класс
Графики тригонометрических функций. 10 класс Отношения и пропорция
Отношения и пропорция Логарифмические уравнения и неравенства. Практическая работа
Логарифмические уравнения и неравенства. Практическая работа Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Практическое занятие №7 Минимизация логического автомата
Практическое занятие №7 Минимизация логического автомата Вырезаем квадрат
Вырезаем квадрат Подготовка к контрольной работе за полугодие
Подготовка к контрольной работе за полугодие Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Многочлен и его стандартный вид
Многочлен и его стандартный вид Презентация на тему Параллельность прямых и плоскостей (10 класс)
Презентация на тему Параллельность прямых и плоскостей (10 класс)  Параллельные прямые. Задачи для подготовки к контрольной работе
Параллельные прямые. Задачи для подготовки к контрольной работе Пространственные векторы в асинхронном двигателе. Эйлер (1707-1783 гг)
Пространственные векторы в асинхронном двигателе. Эйлер (1707-1783 гг) Карточки по математике
Карточки по математике Математическое и сенсорное развитие детей раннего возраста
Математическое и сенсорное развитие детей раннего возраста Методика изучения длины
Методика изучения длины Математическая статистика
Математическая статистика Показатели вариации
Показатели вариации Случаи вычитания 11-
Случаи вычитания 11- Задачи на функции
Задачи на функции Сечение многогранников. Применение интерактивных методов обучения на уроках математики
Сечение многогранников. Применение интерактивных методов обучения на уроках математики Физико-математических КВН
Физико-математических КВН Группа предметов. Множество. Элемент множества. 3 класс
Группа предметов. Множество. Элемент множества. 3 класс Материал для внеклассной работы по математике. Бедный заяц (сказка)
Материал для внеклассной работы по математике. Бедный заяц (сказка) Презентация на тему Решение систем уравнений методом новой переменной
Презентация на тему Решение систем уравнений методом новой переменной  Золотое сечение. 9 класс
Золотое сечение. 9 класс Обратные задачи
Обратные задачи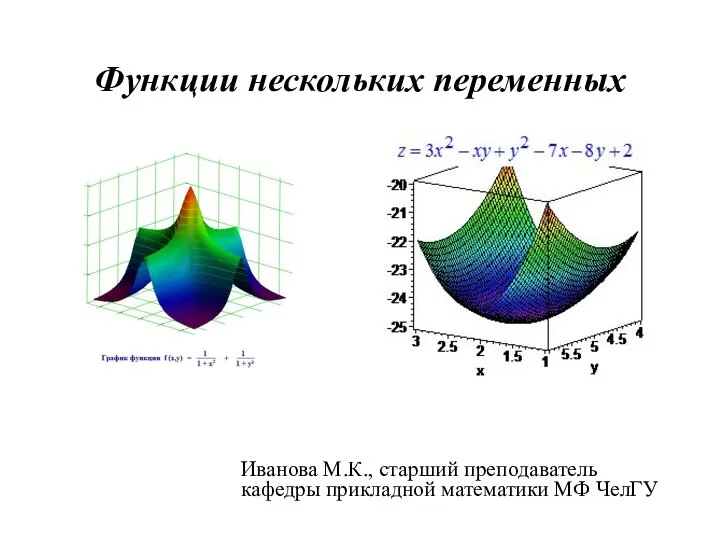 Функции нескольких переменных
Функции нескольких переменных