Содержание
- 2. Вспомним физический смысл производной. материальная точка s(t) закон движения
- 3. Задача: Точка движется прямолинейно по закону s(t) = t3+ 2t ( где s(t) – измеряется в
- 4. Задача: По прямой движется материальная точка, скорость которой в момент времени t задается формулой v(t) =
- 5. При решении задачи, мы, зная производную функции, восстановили ее первичный образ. Эта операция восстановления - операция
- 6. y = F(x) называют первообразной для y = f(x) на промежутке X, если при x ∈
- 7. Операция дифферен-цирования функция y = F(х) (первообразная) y = f(х) производная Операция интегри- рования В математике
- 8. Запомните: Первообразная – это родитель производной:
- 9. Задача: Найдите все первообразные для функций: f(х)=3 f(х)= х2 f(х)=cosx f(х)=12 f(х)=х5
- 10. Три правила нахождения первообразных Если функции у=f(x) и у=g(x) имеют на промежутке первообразные соответственно у=F(x) и
- 13. Скачать презентацию










 Презентация на тему Понятие площади фигуры и ее измерение
Презентация на тему Понятие площади фигуры и ее измерение  Письмо цифры 6
Письмо цифры 6 Задачи по геометрии
Задачи по геометрии Стереометрия. Геометрия
Стереометрия. Геометрия Открытое акционерное общество в 6 классе
Открытое акционерное общество в 6 классе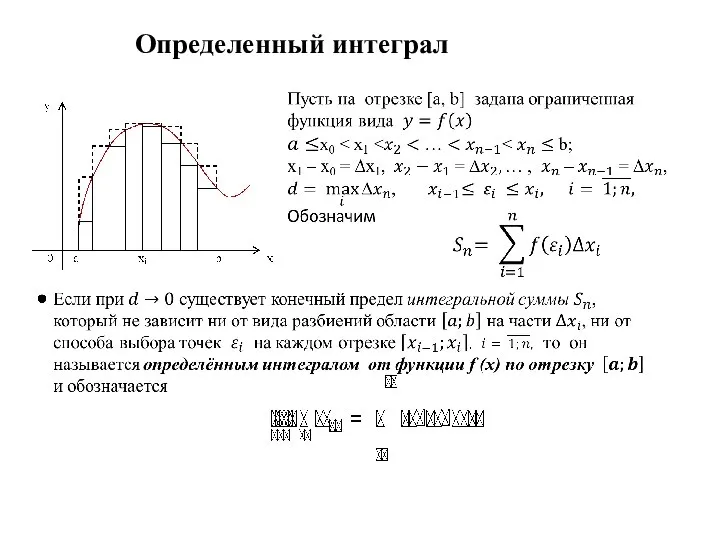 Определённый интеграл
Определённый интеграл Разметка прямоугольника по угольнику
Разметка прямоугольника по угольнику Суждение, как форма мышления. Классификация
Суждение, как форма мышления. Классификация Квадратичная функция
Квадратичная функция Обобщение пропорции и лекарственные растения Сибири
Обобщение пропорции и лекарственные растения Сибири Урок-КВН
Урок-КВН Названия чисел в записях действий
Названия чисел в записях действий Подготовка к контрольной работе. Уравнения
Подготовка к контрольной работе. Уравнения Интерактивная игра-тренажёр. Считаем с Лунтиком (2 класс). Умножение и деление на 5
Интерактивная игра-тренажёр. Считаем с Лунтиком (2 класс). Умножение и деление на 5 Математическое обеспечение (МО) цифрового (автоматизированного) проектирования
Математическое обеспечение (МО) цифрового (автоматизированного) проектирования Площади фигур
Площади фигур Какие бывают графы
Какие бывают графы Понятие цилиндра
Понятие цилиндра Степенная функция и её график
Степенная функция и её график Формула полной вероятности и формула Байеса. Формула Бернулли. Лекция 3
Формула полной вероятности и формула Байеса. Формула Бернулли. Лекция 3 Задачи для подготовки к контрольной работе
Задачи для подготовки к контрольной работе Решение треугольников
Решение треугольников Устный счёт. Назови числа по порядку
Устный счёт. Назови числа по порядку Entrant
Entrant Угол между векторами (часть 2)
Угол между векторами (часть 2) Сложение +5
Сложение +5 Формирование алгоритмического мышления у младших школьников
Формирование алгоритмического мышления у младших школьников Презентация на тему Величины (4 класс)
Презентация на тему Величины (4 класс)