Слайд 2 Если вы хотите участвовать в большой жизни, то наполняйте свою голову

математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе.
М.И. Калинин
Слайд 4 Основные тождественные преобразования.
Перестановка местами слагаемых, множителей.
Раскрытие скобок.
Группировка слагаемых,

множителей.
Замена разностей суммами, частных произведениями и обратно.
Выполнение действий с числами
Вынесение за скобки общего множителя.
Приведение подобных слагаемых.
Замена чисел и выражений тождественно равными им выражениями.
Прибавление и вычитание одного и того же числа.
Слайд 5 Рассмотрим задачи на вычисление значений выражений.
Пример №1:
Вычислите произведение:

(2 + 1)(22 + 1)(24 + 1)(28 + 1)(216 + 1)(232 + 1).
Решение:
Заметим, что значение первой скобки (2 + 1)=3, если умножить первую скобку на выражение (2-1), то получится формула сокращенного умножения разность квадратов
и значение будет равно 3.
Итак, умножим наше выражение на (2 – 1) и применим формулу разности квадратов 6 раз. Получим:
Слайд 6
(2 -1)(2 + 1)(22 + 1)(24 + 1)(28 + 1)
(216 +

1)(232 + 1) = (22 – 1)(22 + 1)(24 + 1)
(28 + 1)(216 + 1)(232 + 1) = (24 – 1)(24 + 1)
(28 + 1)(216 + 1)(232 + 1) = (28 – 1)(28 + 1)
(216 + 1)(232 + 1) = (216 – 1)(216 + 1)(232 + 1) = (232 – 1)(232 + 1) = (264 – 1).
Ответ: (264 – 1).
Слайд 7 Пример №2:
Вычислите произведение:
Р =
Решение:
Упростим это выражение:
Р = =

Слайд 8 Полученное произведение можно сократить на
2 • З2 • 42 • 52

(n — 1)2 • n.
После этого будем иметь:
Р =
Ответ:
Слайд 9Пример №3:
Упростите сумму:
1 • 1! + 2 • 2! + 3

• 3! + ... + n• n!
Решение:
Вспомним, что такое факториал.
Факториал числа – это произведение натуральных чисел от 1 до самого числа (включая данное число). Обозначается факториал (!).
Например: 3! = 1∙2∙3=6
6! =1∙2∙3∙4∙5∙6=720
Запомни факториал 0 и 1 равен 1 (0!=1 и 1!=1).
Слайд 10 Итак, прибавим к данной сумме 1 и используем тождество K!+KK! =

(K+1)!, а затем вычтем 1.
Получим:
1+1∙1!+2∙2!+3∙3!+…+n∙n! =
(1+1)!+2∙2!+3∙3!+…+ n∙n! =
2!+2∙2!+3∙3!+…+ n∙n! =
(2+1)!+3∙3!+…+ n∙n!=
3!+3∙3!+…+ n∙n!=
(1+3)!+…+ n∙n!=
4!+…+ n∙n!=(n+1)!
Вычитая 1 получим: (n+1)! – 1.
Ответ: (n+1)! – 1.
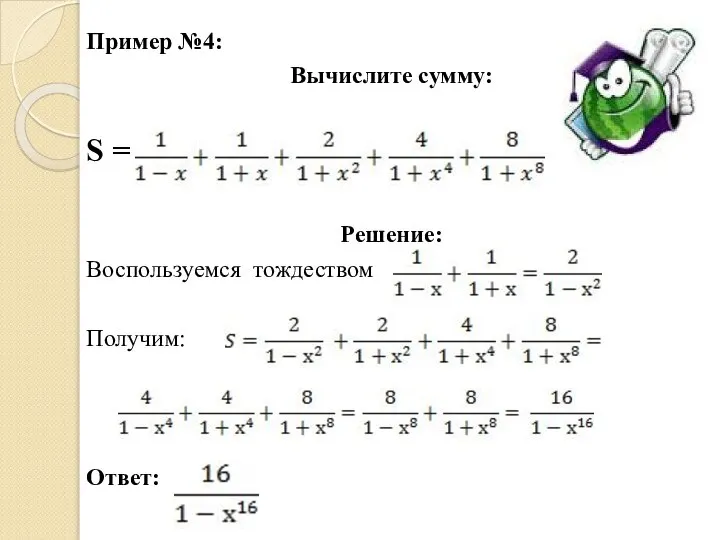
Слайд 11Пример №4:
Вычислите сумму:
S = .
Решение:
Воспользуемся тождеством
Получим:
Ответ:
Слайд 12Пример №5:
Вычислите сумму:
S=
Решение:
Приведем сумму к общему знаменателю (a-b)(b-c)(c-a):
S=

=
Ответ: 0.
Слайд 13Пример №6:
Вычислите сумму:
Решение:
Приведем сумму к общему знаменателю (a-b)(b-c)(c-a):
Ответ: 0.

Слайд 14Пример №7:
Вычислите сумму:
Решение:
Заметим, что данное выражение имеет смысл при a≠b,

a≠с, b≠c. Будем проводить преобразования для таких значений переменных. Приведя все дроби к наименьшему общему знаменателю, получим:
Слайд 15 Заметив, что b-c=(a-c)-(a-b) , преобразуем числитель следующим образом:
a2(b-c) –

b2(a-c)+c2(a-b)=a2(a-c) – a2(a-b) – b2(a-c)+c2(a-b) =(a-c)(a-b)(a+b-c-a) =
(a-b)(b-c)(a-c).
Таким образом, получили:
= 1
Ответ: 1.
Слайд 16Пример №8:
Вычислите сумму:
1 + 11 + 111 + … +

111...1 (n слагаемых).
Решение:
Заметим, что 1=(10-1)/9, 11=(100-1)/9, 111=
(1000-1)/9,...11...1(n единиц) =(10n-1)/9,
Тогда искомая сумма
S = 1/9(10+100+1000+...+10n - n) = 1/9(Sn - n), где Sn - сумма геометрической прогрессии, b1=10, q=10.
Sn = (10n+1-10)/9
S = 1/81 ( 10n+1-9n-10)
Ответ: 1/81 ( 10n+1-9n-10)
Слайд 17Пример №9:
Вычислите сумму:
S=1-2 + 3-4 + - + (-l)n+1∙n.
Решение:
Очевидно,

ответ зависит от четности или нечетности n. Поэтому рассмотрим два случая.
Пусть n четно. Тогда:
S = (1 - 2) + (3 - 4) + (5 - 6) + - + (n - 1) - n) = -1
- 1 - ...- 1 = -
Слайд 182) Пусть n нечетно. Будем иметь:
S = (1 - 2 + 3

- 4 + …- (n - 1)) + n=
Ответ: если n четно, то S = -n/2; если n нечетно, то S = (n + 1)/2.
Подумайте: нельзя ли два полученных выражения для S объединить в
одной формуле?

















 Решение треугольников
Решение треугольников Математика и я
Математика и я Параллелограмм и трапеция
Параллелограмм и трапеция Умножение десятичных дробей
Умножение десятичных дробей Углы. Виды углов
Углы. Виды углов Презентация на тему Решение квадратных уравнений и неравенств
Презентация на тему Решение квадратных уравнений и неравенств  Оценка уровня сформированности информационной компетенции у учащихся на уроках математики
Оценка уровня сформированности информационной компетенции у учащихся на уроках математики Рациональные дроби. 8 класс
Рациональные дроби. 8 класс Решение линейных неравенств
Решение линейных неравенств Свойства корня степени n
Свойства корня степени n Дифференциал функции. Производные высших порядков. Дифференциал функции. Вторая производная и производные высших порядков
Дифференциал функции. Производные высших порядков. Дифференциал функции. Вторая производная и производные высших порядков Вписанные и описанные четырехугольники
Вписанные и описанные четырехугольники Презентация на тему ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИ
Презентация на тему ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИ  Сложение в пределах 20
Сложение в пределах 20 Целое уравнение и его корни. 9 класс
Целое уравнение и его корни. 9 класс Сложение и вычитание с 0
Сложение и вычитание с 0 3_Equations_2
3_Equations_2 Подготовка к ЕГЭ В8
Подготовка к ЕГЭ В8 Определители матриц
Определители матриц Математика. Лекция 3. Векторы. Уравнения плоскости в пространстве
Математика. Лекция 3. Векторы. Уравнения плоскости в пространстве На оптимизацию с решением
На оптимизацию с решением Решение задач на нахождение неизвестного вычитаемого
Решение задач на нахождение неизвестного вычитаемого Правильные и неправильные дроби. Характеристики миномётов
Правильные и неправильные дроби. Характеристики миномётов Презентация на тему Двугранный угол
Презентация на тему Двугранный угол  Презентация на тему Сравнение десятичных дробей
Презентация на тему Сравнение десятичных дробей  Конструктор (4)
Конструктор (4)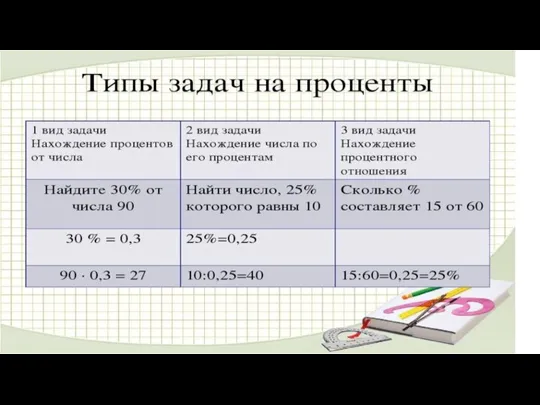 Задачи на проценты
Задачи на проценты Подготовка к контрольной работе
Подготовка к контрольной работе