Показательная функция, ее свойства и график

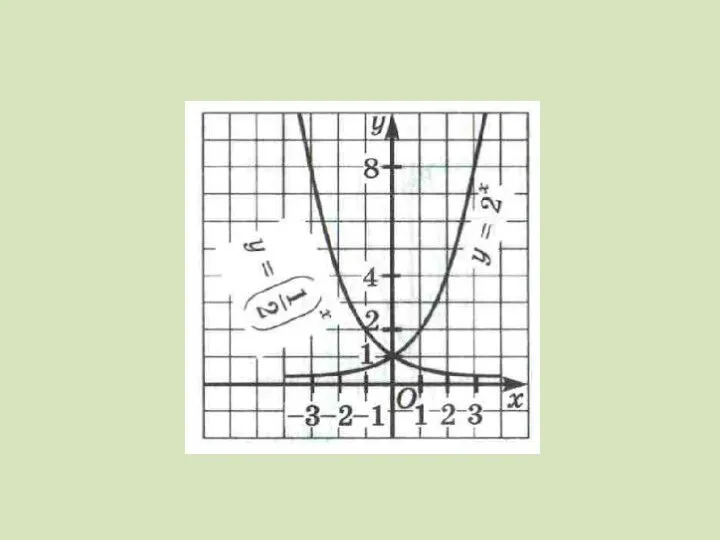
Рассмотрим функцию вида у = 2х, определенную на множестве всех действительных чисел.

График

Свойства функции у = 2х
D(у): х∈(-∞; +∞)
Функция общего вида
Возрастает
Ограничена снизу и не ограничена сверху
Нет ни наибольшего, ни наименьшего значений
Непрерывна
Е(у): у ∈ (0; +∞)
Выпукла вниз

Точно такими же функциями обладает любая функция вида у = ах , где а > 1.

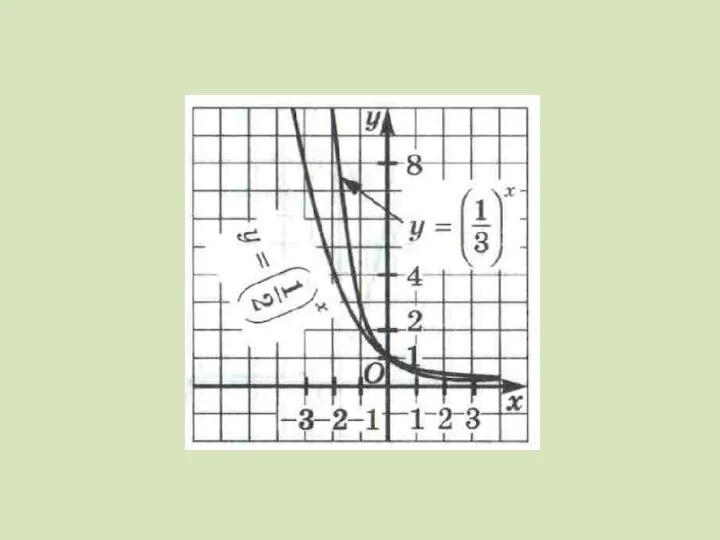
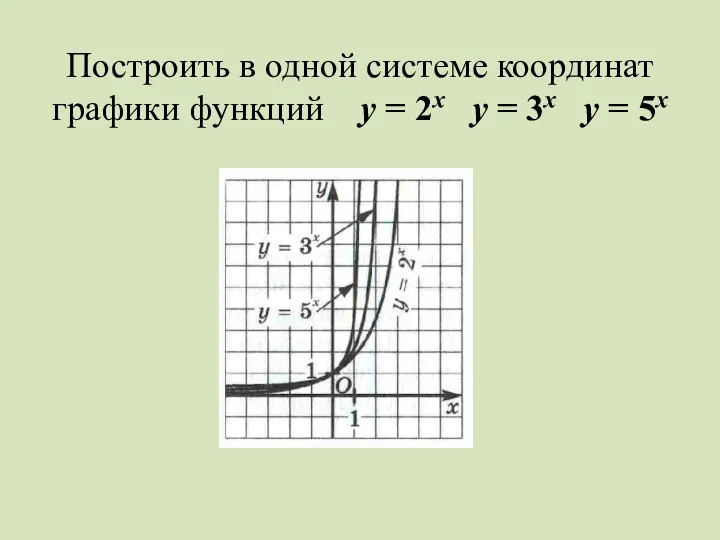
Построить в одной системе координат графики функций у = 2х у = 3х у = 5х

у =
х

D(у): х∈(-∞; +∞)
Функция общего вида
Убывает
Ограничена снизу и не ограничена сверху
Нет ни наибольшего, ни наименьшего значений
Непрерывна
Е(у): у ∈ (0; +∞)
Выпукла вниз

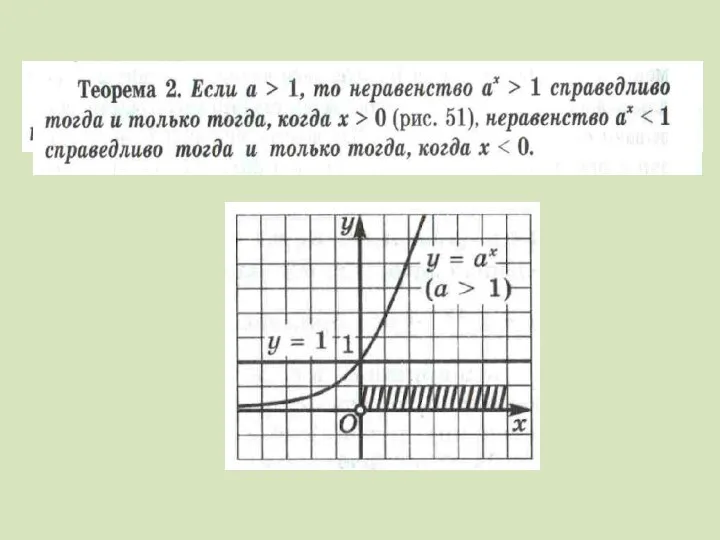
Определение
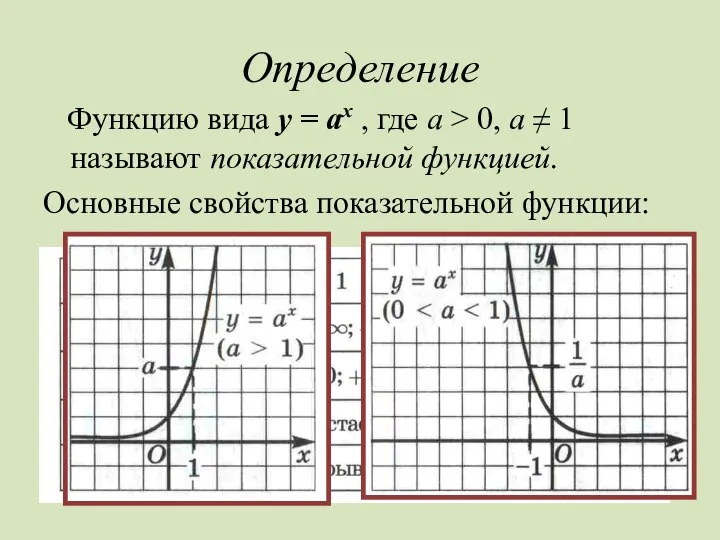
Функцию вида у = ах , где а > 0, а ≠ 1 называют показательной функцией.
Основные свойства показательной функции:

Устная работа.

Устная работа.

Решить уравнения и неравенства

Решить уравнения и неравенства

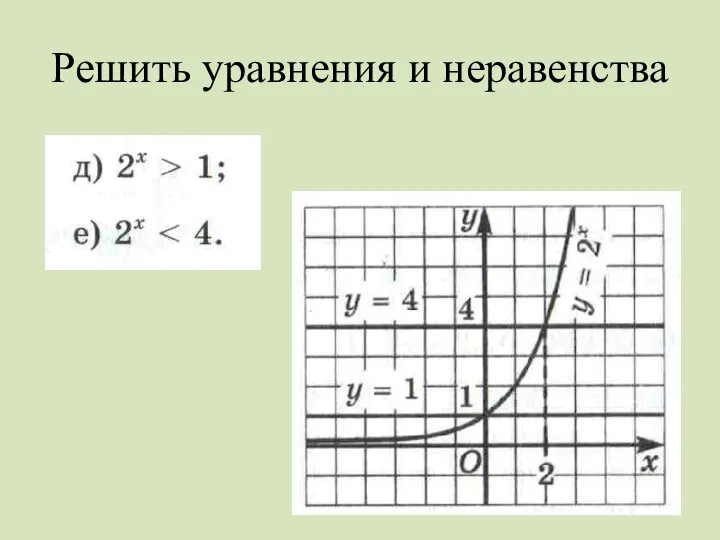
Примеры решения задач по теме
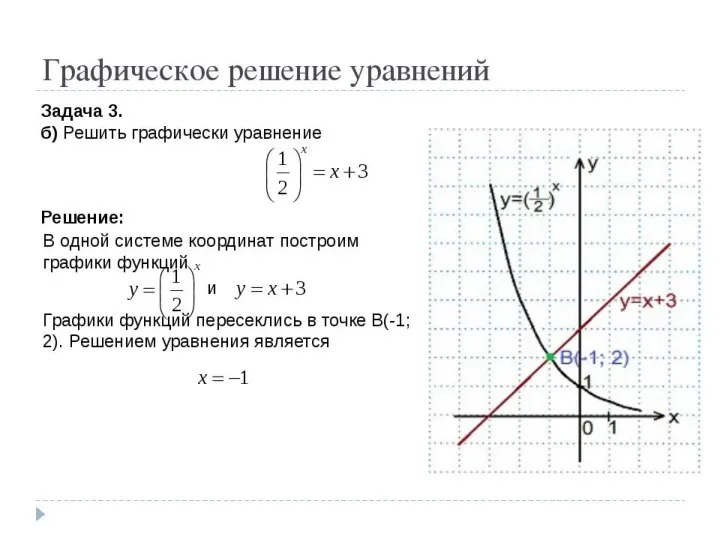
С помощью графиков функций (используя соответствующие свойства функций) можно решать показательные уравнения и неравенства, находить наибольшее и наименьшее значения функции на отрезке.

№ 1. Решите уравнение
воспользуемся тем, что функция y = 2t монотонна (возрастает), поэтому из равенства следует

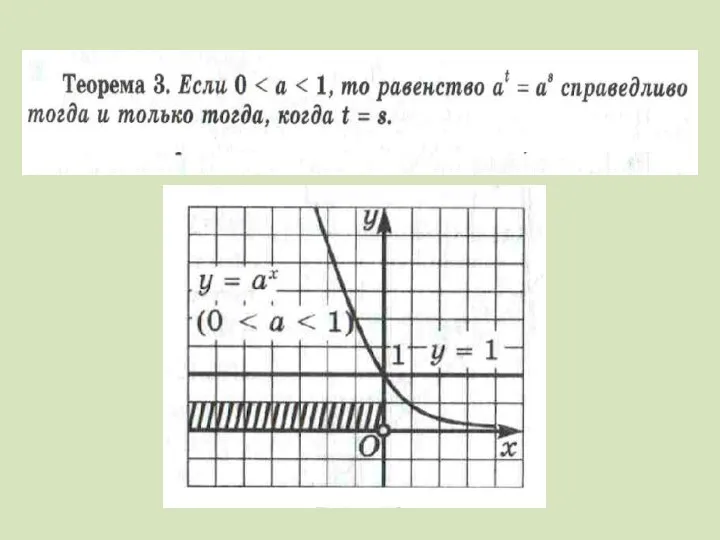
№ 2. Решите неравенство
так как функция y = 8t возрастает при t ≥ 0, то x > 2.