Экстремумы функции

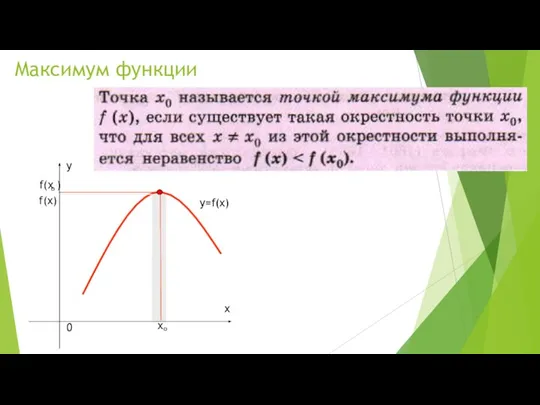
Максимум функции
f(х)
y=f(x)

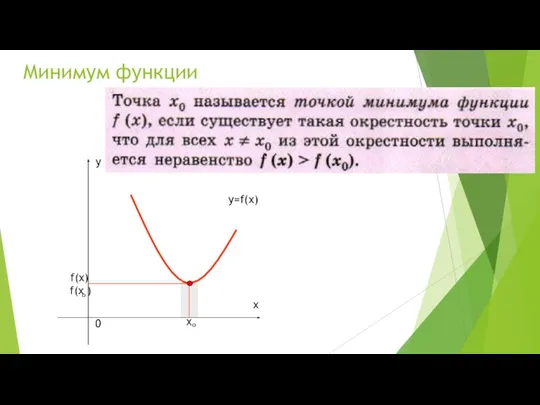
Минимум функции
f(х)
y=f(x)

Точки минимума и максимума
называются точками экстремума функции.
Если х0 - точка экстремума
дифференцируемой функции f(х),
то производная функции в
этой точке f'(х0) = 0.

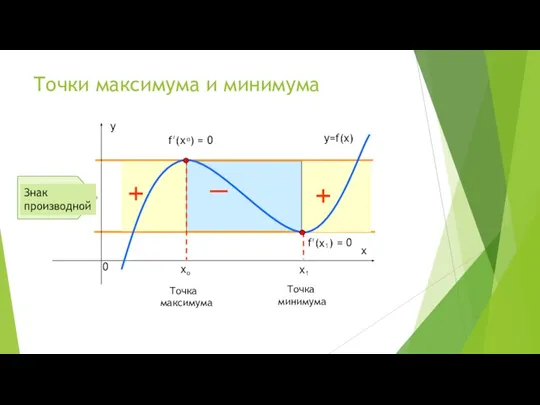
Точки максимума и минимума
_
Точка
максимума
Точка
минимума

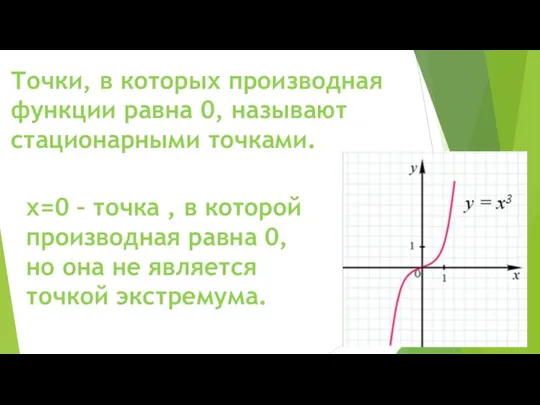
Точки, в которых производная функции равна 0, называют стационарными точками.
х=0 – точка , в которой производная равна 0, но она не является точкой экстремума.

Точки, в которых функция имеет производную, равную 0 или не имеет производной, называют критическими точками.
х=0 – точка минимума, а производной в этой точке нет.

Алгоритм нахождения точек экстремума:
Найти критические точки функции
Найти промежутки возрастания и убывания функции (f′(x)>0 и f′(x)<0))
Критические точки, в окрестности которых производная меняет знак с «+» на «-» - это точки максимума
Критические точки, в окрестности которых производная меняет знак с «-» на «+» - это точки минимума
Для одной функции на некотором промежутке может быть несколько точек экстремума.

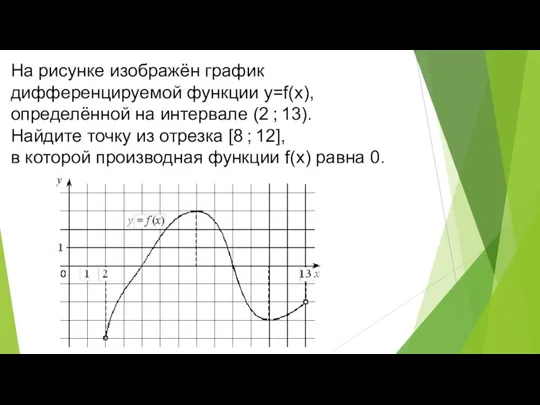
На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (2 ; 13).
Найдите точку из отрезка [8 ; 12],
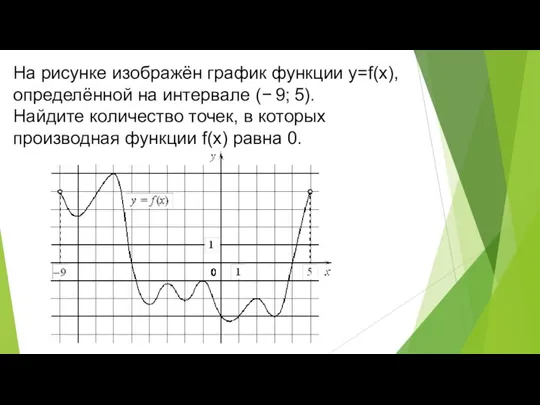
в которой производная функции f(x) равна 0.

На рисунке изображён график функции y=f(x),
определённой на интервале (− 9; 5).
Найдите количество точек, в которых
производная функции f(x) равна 0.

1)функция возрастает на отрезке [− 1; 1]
2)функция убывает на отрезке [− 1; 1]
3)функция имеет точку минимума на отрезке [− 1; 1]
4)функция имеет точку максимума на отрезке [− 1; 1]
А)
Б)
В)
Г)