Содержание
- 2. Проектның гипотезасы: Оригами сәнгате геометрия фәне белән тыгыз бәйлелектә
- 3. Проектның максаты: Геометрия фәне һәм оригами сәнгате арасындагы бәйлелекне күрсәтүче мәгълүмат җыю һәм эшкәртү.
- 4. Проектның дидактик максаты: 1. Геометрия фәненең тормышта кирәклеген ачыклау. 2. Геометриянең оригами сәнгате белән тыгыз бәйлелектә
- 5. Бурычлар: 1) Геометриянеӊ килеп чыгу тарихын өйрәнү; 2) Оригами турында мәгълүмат җыю; 3) Оригами нигезләре һәм
- 6. Эзләү группаларына бүленү 1 нче группа геометрия фәненеӊ килеп чыгу тарихын, аӊа нигез салучы математикларны, 2
- 7. Аннотация Проектны «Турыпочмаклык, ромб, квадрат», «Күчәргә карата һәм үзәккә карата симметрия», «Өчпочмакныӊ медианасы, биссектрисасы һәм биеклеге»
- 8. Эчтәлек Геометрия фәненеӊ килеп чыгу тарихы Оригами сәнгате турында Геометрия фәне һәм оригами сәнгатендә аксиомалар охшашлыгы
- 9. Геометрия фәненең килеп чыгу тарихы «Геометрия» сүзенеӊ грекчадан тәрҗемәсе («гео» - җир, ә «метрио» - үлчәү)
- 10. Иӊ гади геометрик мәгүлүматларны үз эченә алган беренче кулъязма Борынгы Мисырда язылган.
- 11. Евклидныӊ (б.э.к. якынча 300 еллар) “Башлангычлар” (“Начала”) дип аталган атаклы әсәрендә ул вакытта билгеле булган төп
- 12. Геометриянеӊ төрле мәсьәләләрен тикшерүгә Архимед (б.э.к. якынча 287-212 еллар), Аполлоний (б.э.к. III гасыр) һәм башка борынгы
- 13. Р.Декарт, координаталар методы кертеп, геометрияне алгебра белән бәйләүгә ирешкән Рене Декарт (1596-1650)
- 14. Евклид геометриясеннән башка геометрия төзи, аны Лобачевский геометриясе дип атыйлар Н.И.Лобачевский (1792-1856)
- 15. “Ори” – бөкләү, “ками” кәгазь дигәнне аңлата. Туган иле – Япония. Оригами әлифбасын беренчеләрдән булып япон
- 16. Садако Сасаки турында риваять Садако Сасаки (1943-1955) Маленьких журавликов весёлых Из листа бумаги разноцветной Девочка упорно
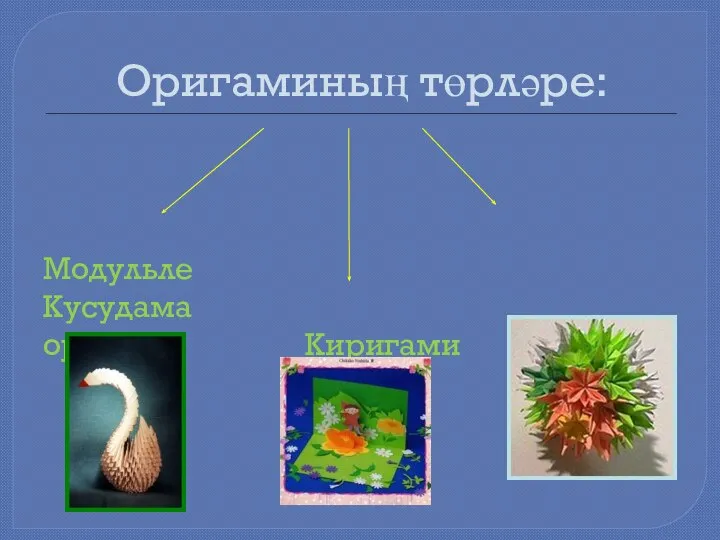
- 17. Оригаминың төрләре: Модульле Кусудама оригами Киригами
- 18. Геометрия һәм оригамидагы аксиомалар охшашлыгы Аксиома 1. Ике нокта аша бердәнбер бөкләү эшләнелә. (Существует единственный сгиб,
- 19. Аксиома 3. Ике турыны берләштерүче бердәнбер бөкләү эшләнелә. ( Существует сгиб, совмещающий две данные прямые) Аксиома
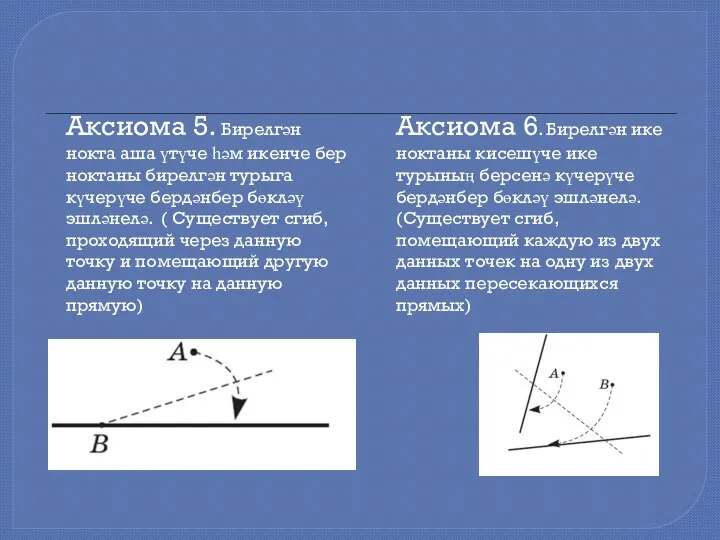
- 20. Аксиома 5. Бирелгән нокта аша үтүче һәм икенче бер ноктаны бирелгән турыга күчерүче бердәнбер бөкләү эшләнелә.
- 22. Скачать презентацию

















 Алгебраическая кривая
Алгебраическая кривая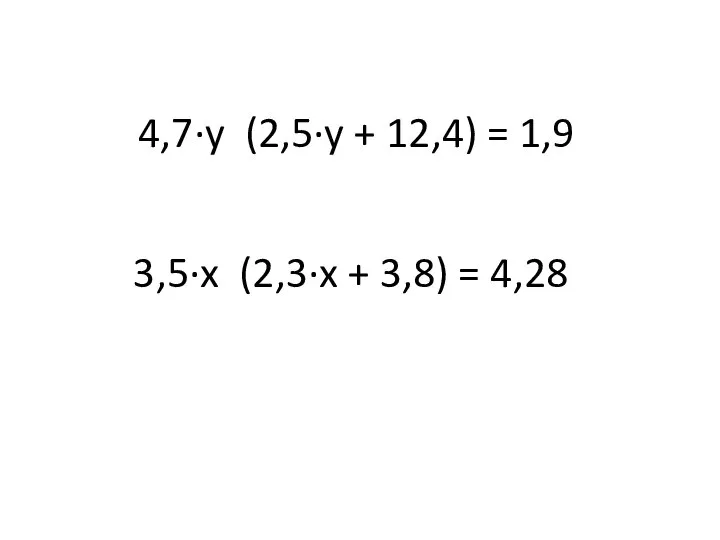 Учение о десятичных дробях
Учение о десятичных дробях Метод наименьших квадратов
Метод наименьших квадратов Случайные сигналы и их математические модели
Случайные сигналы и их математические модели Какая фигура лишняя?
Какая фигура лишняя? Пифагор и его школа
Пифагор и его школа Міри центральної тенденції
Міри центральної тенденції ОГЭ 2020-21. Задание №9. Найдите корень уравнения
ОГЭ 2020-21. Задание №9. Найдите корень уравнения Умножение и деление смешанных чисел
Умножение и деление смешанных чисел Производная в химии
Производная в химии Презентация на тему Натуральные числа 5 класс
Презентация на тему Натуральные числа 5 класс  Математические ребусы (1 класс)
Математические ребусы (1 класс) Решение системы линейных уравнений. Методы решения системы линейных уравнений
Решение системы линейных уравнений. Методы решения системы линейных уравнений Умножение и деление десятичных дробей
Умножение и деление десятичных дробей Непрерывность функции на отрезке
Непрерывность функции на отрезке Вычисление определенных интегралов (Занятие №6)
Вычисление определенных интегралов (Занятие №6) Решение экономических задач
Решение экономических задач Запись многозначных чисел
Запись многозначных чисел Критериальная система и методика оценивания геометрических заданий 23, 24, 25 модуля Геометрия
Критериальная система и методика оценивания геометрических заданий 23, 24, 25 модуля Геометрия Конустун бетинин аянты
Конустун бетинин аянты 1-2_1
1-2_1 Презентация на тему Умножение многочленов (7 класс)
Презентация на тему Умножение многочленов (7 класс)  Решение квадратных уравнений выделением квадрата двучлена
Решение квадратных уравнений выделением квадрата двучлена Векторная алгебра. Расчет модели
Векторная алгебра. Расчет модели Прямоугольник. Ось симметрии
Прямоугольник. Ось симметрии Окружность в аксонометрии. 8 класс
Окружность в аксонометрии. 8 класс Решение уравнений: рациональных и иррациональных
Решение уравнений: рациональных и иррациональных Лекция 2
Лекция 2