Содержание
- 2. 1. Определения и примеры Лемма 1.1: Пусть S – подмножество векторного пространства V, тогда ∀ v
- 3. Пример 1.2: Пусть Тогда так как Определение 1.3: Линейная независимость Подмножество векторного пространства линейно независимо, если
- 4. Лемма 1.4: Практический тест для определения ЛН. есть ЛН т.и т.т.к. → Доказательство ⇒ : Если
- 5. Пример 1.5: Строки { (40 15), (−50 25) } являются ЛН. Доказательство: Пусть → → →
- 6. Лемма 1.6: Пустое подмножество является ЛН. Лемма 1.7: Любое подмножество S содержащее 0, является ЛЗ. Доказательство:
- 7. Лемма 1.9: Всякое подмножество ЛН множества является также ЛН. Всякое надмножество ЛЗ множества также является ЛЗ.
- 9. Скачать презентацию






 Credit and exam
Credit and exam Создание геометрических тел
Создание геометрических тел Переход от передаточных функций к дифференциальным уравнениям и структурным схемам
Переход от передаточных функций к дифференциальным уравнениям и структурным схемам Поверхности второго порядка
Поверхности второго порядка Решение задач по теории вероятности. Подготовка к ГИА
Решение задач по теории вероятности. Подготовка к ГИА Старинные русские меры длины
Старинные русские меры длины Сочетания. В чем отличие от размещений?
Сочетания. В чем отличие от размещений? Устный счет
Устный счет Основы теории графов
Основы теории графов Урок математики в 1 классе
Урок математики в 1 классе Сравнение десятичных дробей
Сравнение десятичных дробей Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ
Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ  Педагогические приемы включения детей, имеющих нарушения слуха, в образовательное пространство урока математики
Педагогические приемы включения детей, имеющих нарушения слуха, в образовательное пространство урока математики Система MatLab/ Методические указания к выполнению лабораторных работ
Система MatLab/ Методические указания к выполнению лабораторных работ Рисование узора из геометрических фигур
Рисование узора из геометрических фигур Треугольники в окружающем мире
Треугольники в окружающем мире Метод группировки
Метод группировки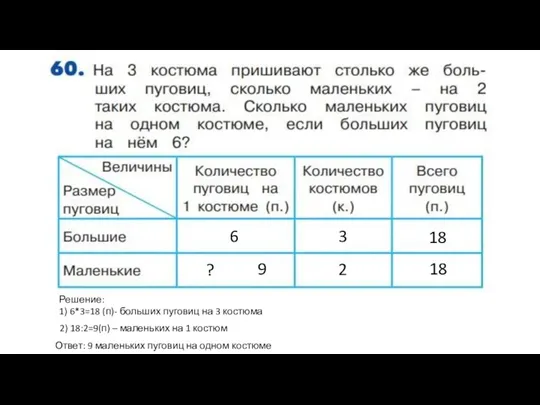 Задача о костюмах
Задача о костюмах Основы теории оболочек вращения
Основы теории оболочек вращения Знакомство с цифрой 5
Знакомство с цифрой 5 Линии и углы в окружности
Линии и углы в окружности Формирование знаковой культуры на уроках
Формирование знаковой культуры на уроках Статистическое наблюдение
Статистическое наблюдение Формула Остроградского - Гаусса
Формула Остроградского - Гаусса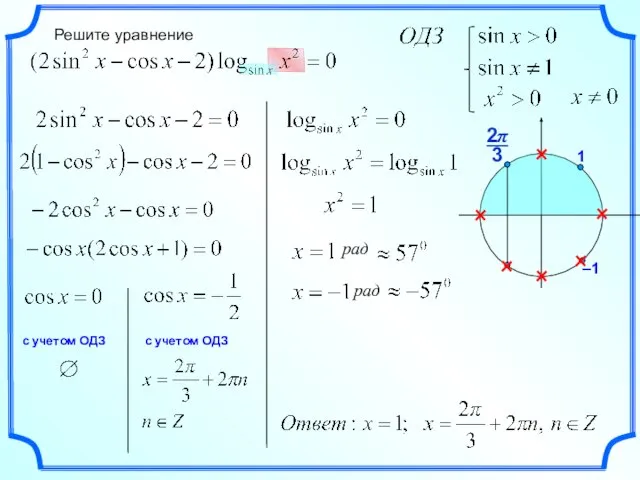 Решение уравнения
Решение уравнения Приемы устного счета
Приемы устного счета Вычисление неопределенного интеграла
Вычисление неопределенного интеграла Состав числа 10
Состав числа 10