Построение таблиц истинности

Укажите названия следующих логических операций:
А. ¬
Б. &
В. v
Г. ↔
Д. →
1

Укажите знаки логических операций, которым в русском языке соответствует:
А. Союз «и»
Б. Союз «или»
В. Частица «не»
Г. Оборот речи «тогда и только тогда, когда»
Д. Оборот речи «если, то»
2

Запишите название логических операций:
А. Логическое следование
Б. Логическое сложение
В. логическое равенство
Г. Логическое умножение
Д. Отрицание
3

Укажите название логической операции, для которой верно утверждение:
А.Истинна ↔, когда все переменные истинны
Б. Ложна ↔, когда из истины следует ложь
В. Истинна, когда переменные имеют одинаковые значения
Г. Ложна ↔, все переменные ложны
Д. Истинна, когда переменная ложна и наоборот
4

Перечислите логические операции в соответствии с их приоритетом
5

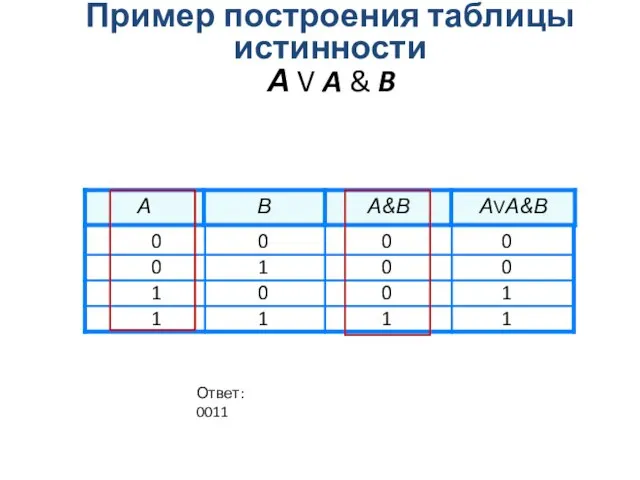
А V A & B
Пример построения таблицы истинности
0 0
0 1
1 0
1 1
0
0
0
1
0
0
1
1
Ответ: 0011

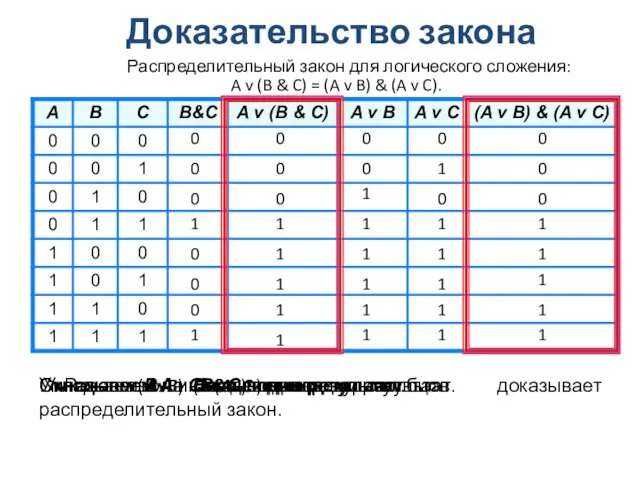
Распределительный закон для логического сложения:
A v (B & C) = (A v B) & (A v C).
Доказательство закона
Умножаем В на С и выводим результат.
0
0
0
0
0
0
1
1
Складываем А и В и выводим результат.
0
0
0
1
1
1
1
1
Складываем А и (В&С) и выводим результат.
0
0
1
1
1
1
1
1
Складываем А и C и выводим результат.
0
0
1
1
1
1
1
1
Умножаем (АvB) на (AvC )и выводим результат.
0
0
0
1
1
1
1
1
Равенство выделенных столбцов доказывает распределительный закон.

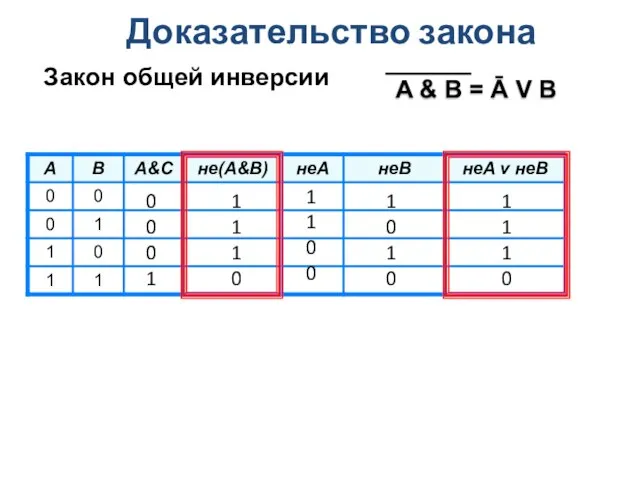
Доказательство закона
Закон общей инверсии
0
0
0
1
1
1
1
0
1
1
0
0
1
0
1
0
1
1
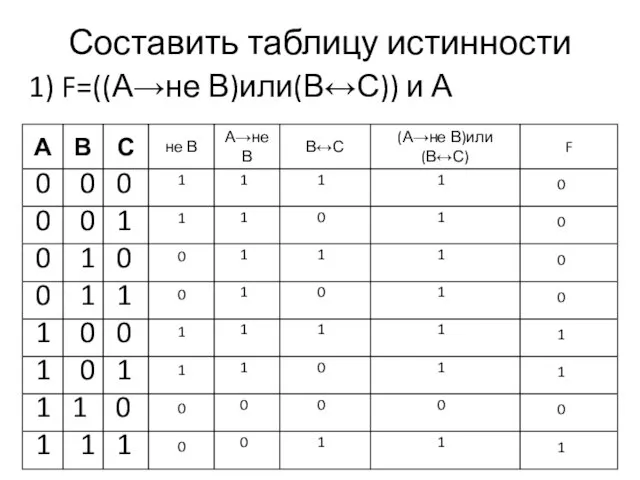
1
0

Составить таблицу истинности
1) F=((А→не В)или(В↔С)) и А
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 0
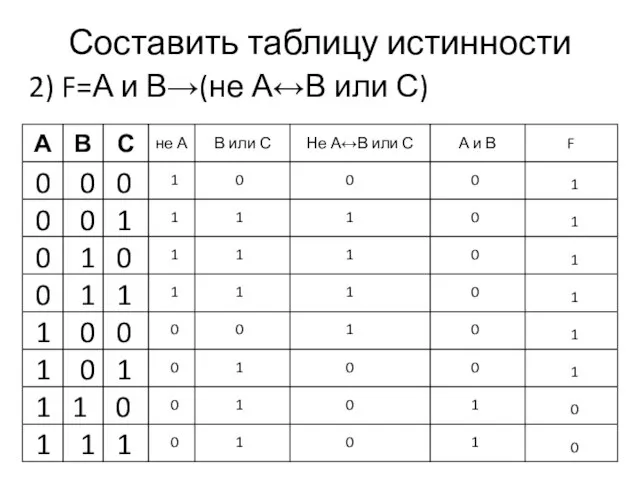
1 1 1

Составить таблицу истинности
2) F=А и В→(не А↔В или С)
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 0
1 1 1